对称多项式不等式的“物理证明”
By 苏剑林 | 2011-08-13 | 46298位读者 | 引用本文将再次谈到对称这个话题,不过这一次的对象不是“等式”,而是“不等式”。
在数学研究中,我们经常会遇到各种各样的函数式子,其中有相当一部分是“对称”的。什么是对称的函数呢?对称有很多种说法,但是针对于多元对称式,我们的定义为满足$f(x_1,x_2,...,x_n)=f(y_1,y_2,...,y_n)$的函数,其中$(y_1,y_2,...,y_n)$是$(x_1,x_2,...,x_n)$的任意一个排列。通俗来讲,就是将式子中任意两个未知数交换位置,得到的式子还是和原来的式子一样。例如$\sin x+\sin y$,把$x,y$交换位置后得到$\sin y+\sin x$,还是和原来的一样;再如$xy+yz+zx$,将y,z互换后可以得到$xz+zy+yx$,结果还是和原式一样;等等。有些对称的函数是一个n次的多项式,那么就叫它为n次对称多项式,上边的例子$xz+zy+yx$就是一个三元二次对称多项式。
八月一号开始我们这里的高三就正式开学了,以后每周都只能在星期天中午到下午的一小段时间里跟读者们见见面了^_^
高三的生活的确很枯燥、烦闷,特别是老师那句重复了无数遍的话“这个知识点在高考是这样出题的...”让我感觉十分讨厌,难道,学习就为了高考?就算真的是难以改变的现状,我也偏不服从。高考是要准备的,“活”也是要“生”的,为了生活而生存,而不是为了生存而生活。
虽然很忙,但我还是会抽一些时间出来研究自己感兴趣的东西的,如研究一下几何、不等式、多项式、对称等等,还有发一下呆^_^,当然也尽可能抽一些时间来这里写写我的学习心得吧——当然,频率应该会很低。
我相信,一年之后我不会后悔的。
IMO42-1,我也会做几何题
By 苏剑林 | 2011-07-30 | 36553位读者 | 引用七月再次“农忙”,农村里要插秧了,播下种苗,等待再次收获的季节^_^
我一直觉得我的数学能力偏向于分析计算而不擅长于几何,纵使遇到几何问题,也是满脑子的解析几何做法,没有纯几何的美。而这几天为了加强数学竞赛题目的能力,我一直在看IMO的题目,并且企图独立做出一些题目,但都无果。我比较感兴趣的是不等式,我感觉一道简单的式子,不用太多的文字就可以讲清楚的题目非不等式莫属,但是IMO的不等式题实在高深,我还没有能够独立做出一道来(参考答案可以看懂,只是想不到思路),或许是我在努力追求统一的方法而不肯研究那些特定的技巧的原因吧。不料今天看了一下2001年IMO的几何题目,发现我可能将它做出来,于是研究了一会,最终很幸运地做了出来。虽然不是最简单的方法,但也与大家分享一下。
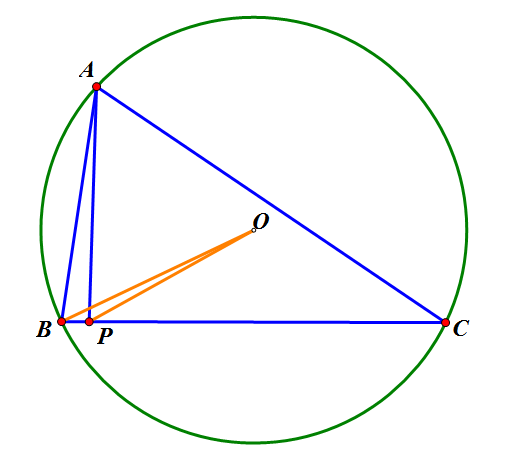
如图,O是锐角三角形ABC的外心,AP是三角形的垂线段,∠B-∠C不小于30°。证明∠BAC+∠BOP < 90°
Lamost下的天文夏令营
By 苏剑林 | 2011-07-27 | 19838位读者 | 引用科学空间:2011年8月重要天象
By 苏剑林 | 2011-07-27 | 21577位读者 | 引用在农村,7月是忙碌的月份,农民们要忙着收割稻谷,收割完后要晒谷,同时还得准备“下秧”,准备新一轮的耕,BoJone家自然也不例外。不过我家田比较少(1亩左右),收割机几分钟搞定,谷也三两天就晒完了。不过在晒谷的时候,BoJone在考虑一个“收谷”问题:
晒谷时得先把成堆的谷子摊开,薄薄地平铺在平地上,等到傍晚或即将下雨时(这是最惨的情况,搞不好会淋谷)就将其收起来。问题就源于这里,一般来说我们会把谷均匀地铺成矩形,要把所有的谷都推到矩形里或外的哪一点上,才使得我们做功做小?
这个问题还可以推广开来,例如对于一地任意形状的谷子(如三角形),把它集中堆到哪个点最“轻松”?一堆固定质量的谷子,要把它平铺成什么形状,才使得收谷时最“轻松”?当然,这个问题的解不仅仅用于“收谷”,在很多规划建设中也可以应用到,例如要在一个人口大致均匀的城市中建设一个服务中心,这个服务中心应该建在哪里?这有点类似于我们之前讨论过的费马点问题 ,都是费马点只考虑了三个点的距离,而这个问题得考虑所有点的距离。
关于e,i,π的那些鲜为人知的事儿...
By 苏剑林 | 2011-07-25 | 63493位读者 | 引用学着《还珠格格3之天上人间》中的情节,今天我也把自己书架上的书搬上楼去晒晒。
有的书是新买的,有的已经买了一两年了,不管怎样,都拿上去沐浴阳光。
后来才发现,把书搬上去很累很热,把书搬下来重新整理更累更热。整个过程从早上九点开始,直到下午两点才完全结束。
原来,把书搬到太阳下展开的场景很壮观......
当然,晒书只是一个契机,我顺便收拾了一下凌乱的房间,这次算是比较彻底了,一些平常没有清洁的角落都清理了一遍。因为再过几天就正式成为高三了。也许下一次晒书,或者下一次整理,已经是明年的今天了。所以不论怎样,今天都要好好“干一场”!
书籍是人类进步的阶梯,呵呵^_^









最近评论