生成扩散模型漫谈(四):DDIM = 高观点DDPM
By 苏剑林 | 2022-07-27 | 395896位读者 |相信很多读者都听说过甚至读过克莱因的《高观点下的初等数学》这套书,顾名思义,这是在学到了更深入、更完备的数学知识后,从更高的视角重新审视过往学过的初等数学,以得到更全面的认知,甚至达到温故而知新的效果。类似的书籍还有很多,比如《重温微积分》、《复分析:可视化方法》等。
回到扩散模型,目前我们已经通过三篇文章从不同视角去解读了DDPM,那么它是否也存在一个更高的理解视角,让我们能从中得到新的收获呢?当然有,《Denoising Diffusion Implicit Models》介绍的DDIM模型就是经典的案例,本文一起来欣赏它。
思路分析 #
在《生成扩散模型漫谈(三):DDPM = 贝叶斯 + 去噪》中,我们提到过该文章所介绍的推导跟DDIM紧密相关。具体来说,文章的推导路线可以简单归纳如下:
\begin{equation}p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})\xrightarrow{\text{推导}}p(\boldsymbol{x}_t|\boldsymbol{x}_0)\xrightarrow{\text{推导}}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)\xrightarrow{\text{近似}}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)\end{equation}
这个过程是一步步递进的。然而,我们发现最终结果有着两个特点:
1、损失函数只依赖于$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$;
2、采样过程只依赖于$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$。
也就是说,尽管整个过程是以$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$为出发点一步步往前推的,但是从结果上来看,压根儿就没$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$的事。那么,我们大胆地“异想天开”一下:
高观点1: 既然结果跟$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$无关,可不可以干脆“过河拆桥”,将$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$从整个推导过程中去掉?
DDIM正是这个“异想天开”的产物!
待定系数 #
可能有读者会想,根据上一篇文章所用的贝叶斯定理
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \frac{p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)}{p(\boldsymbol{x}_t|\boldsymbol{x}_0)}\end{equation}
没有给定$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$怎么能得到$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$?这其实是思维过于定式了,理论上在没有给定$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$的情况下,$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$的解空间更大,某种意义上来说是更加容易推导,此时它只需要满足边际分布条件:
\begin{equation}\int p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) p(\boldsymbol{x}_t|\boldsymbol{x}_0) d\boldsymbol{x}_t = p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)\label{eq:margin}\end{equation}
我们用待定系数法来求解这个方程。在上一篇文章中,所解出的$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$是一个正态分布,所以这一次我们可以更一般地设
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \mathcal{N}(\boldsymbol{x}_{t-1}; \kappa_t \boldsymbol{x}_t + \lambda_t \boldsymbol{x}_0, \sigma_t^2 \boldsymbol{I})\end{equation}
其中$\kappa_t,\lambda_t,\sigma_t$都是待定系数,而为了不重新训练模型,我们不改变$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)$和$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$,于是我们可以列出
\begin{array}{c|c|c}
\hline
\text{记号} & \text{含义} & \text{采样}\\
\hline
p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0) & \mathcal{N}(\boldsymbol{x}_{t-1};\bar{\alpha}_{t-1} \boldsymbol{x}_0,\bar{\beta}_{t-1}^2 \boldsymbol{I}) & \boldsymbol{x}_{t-1} = \bar{\alpha}_{t-1} \boldsymbol{x}_0 + \bar{\beta}_{t-1} \boldsymbol{\varepsilon} \\
\hline
p(\boldsymbol{x}_t|\boldsymbol{x}_0) & \mathcal{N}(\boldsymbol{x}_t;\bar{\alpha}_t \boldsymbol{x}_0,\bar{\beta}_t^2 \boldsymbol{I}) & \boldsymbol{x}_t = \bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}_1 \\
\hline
p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) & \mathcal{N}(\boldsymbol{x}_{t-1}; \kappa_t \boldsymbol{x}_t + \lambda_t \boldsymbol{x}_0, \sigma_t^2 \boldsymbol{I}) & \boldsymbol{x}_{t-1} = \kappa_t \boldsymbol{x}_t + \lambda_t \boldsymbol{x}_0 + \sigma_t \boldsymbol{\varepsilon}_2 \\
\hline
{\begin{array}{c}\int p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) \\
p(\boldsymbol{x}_t|\boldsymbol{x}_0) d\boldsymbol{x}_t\end{array}} & & {\begin{aligned}\boldsymbol{x}_{t-1} =&\, \kappa_t \boldsymbol{x}_t + \lambda_t \boldsymbol{x}_0 + \sigma_t \boldsymbol{\varepsilon}_2 \\
=&\, \kappa_t (\bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}_1) + \lambda_t \boldsymbol{x}_0 + \sigma_t \boldsymbol{\varepsilon}_2 \\
=&\, (\kappa_t \bar{\alpha}_t + \lambda_t) \boldsymbol{x}_0 + (\kappa_t\bar{\beta}_t \boldsymbol{\varepsilon}_1 + \sigma_t \boldsymbol{\varepsilon}_2) \\
\end{aligned}} \\
\hline
\end{array}
其中$\boldsymbol{\varepsilon},\boldsymbol{\varepsilon}_1,\boldsymbol{\varepsilon}_2\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$,并且由正态分布的叠加性我们知道$\kappa_t\bar{\beta}_t \boldsymbol{\varepsilon}_1 + \sigma_t \boldsymbol{\varepsilon}_2\sim \sqrt{\kappa_t^2\bar{\beta}_t^2 + \sigma_t^2} \boldsymbol{\varepsilon}$。对比$\boldsymbol{x}_{t-1}$的两个采样形式,我们发现要想$\eqref{eq:margin}$成立,只需要满足两个方程
\begin{equation}\bar{\alpha}_{t-1} = \kappa_t \bar{\alpha}_t + \lambda_t, \qquad\bar{\beta}_{t-1} = \sqrt{\kappa_t^2\bar{\beta}_t^2 + \sigma_t^2}\end{equation}
可以看到有三个未知数,但只有两个方程,这就是为什么说没有给定$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$时解空间反而更大了。将$\sigma_t$视为可变参数,可以解出
\begin{equation}\kappa_t = \frac{\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t},\qquad \lambda_t = \bar{\alpha}_{t-1} - \frac{\bar{\alpha}_t\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t}\end{equation}
或者写成
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t} \boldsymbol{x}_t + \left(\bar{\alpha}_{t-1} - \frac{\bar{\alpha}_t\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t}\right) \boldsymbol{x}_0, \sigma_t^2 \boldsymbol{I}\right)\label{eq:p-xt-x0}\end{equation}
方便起见,我们约定$\bar{\alpha}_0=1, \bar{\beta}_0=0$。特别地,这个结果并不需要限定$\bar{\alpha}_t^2 + \bar{\beta}_t^2 = 1$,不过为了简化参数设置,同时也为了跟以往的结果对齐,这里还是约定$\bar{\alpha}_t^2 + \bar{\beta}_t^2 = 1$。
一如既往 #
现在我们在只给定$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$、$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)$的情况下,通过待定系数法求解了$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$的一簇解,它带有一个自由参数$\sigma_t$。用《生成扩散模型漫谈(一):DDPM = 拆楼 + 建楼》中的“拆楼-建楼”类比来说,就是我们知道楼会被拆成什么样【$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$、$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)$】,但是不知道每一步怎么拆【$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$】,然后希望能够从中学会每一步怎么建【$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$】。当然,如果我们想看看每一步怎么拆的话,也可以反过来用贝叶斯公式
\begin{equation} p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1}, \boldsymbol{x}_0) = \frac{p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) p(\boldsymbol{x}_t|\boldsymbol{x}_0)}{p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)}\end{equation}
接下来的事情,就跟上一篇文章一模一样了:我们最终想要$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$而不是$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$,所以我们希望用
\begin{equation}\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t) = \frac{1}{\bar{\alpha}_t}\left(\boldsymbol{x}_t - \bar{\beta}_t \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right)\end{equation}
来估计$\boldsymbol{x}_0$,由于没有改动$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$,所以训练所用的目标函数依然是$\left\Vert\boldsymbol{\varepsilon} - \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}, t)\right\Vert^2$(除去权重系数),也就是说训练过程没有改变,我们可以用回DDPM训练好的模型。而用$\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)$替换掉式$\eqref{eq:p-xt-x0}$中的$\boldsymbol{x}_0$后,得到
\begin{equation}\begin{aligned}
p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \approx&\, p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) \\
=&\, \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \left(\bar{\beta}_t - \alpha_t\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right), \sigma_t^2 \boldsymbol{I}\right)
\end{aligned}\label{eq:p-xt-x0-2}\end{equation}
这就求出了生成过程所需要的$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$,其中$\alpha_t=\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}$。它的特点是训练过程没有变化(也就是说最终保存下来的模型没有变化),但生成过程却有一个可变动的参数$\sigma_t$,就是这个参数给DDPM带来了新鲜的结果。
几个例子 #
原则上来说,我们对$\sigma_t$没有过多的约束,但是不同$\sigma_t$的采样过程会呈现出不同的特点,我们举几个例子进行分析。
第一个简单例子就是取$\sigma_t = \frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}$,其中$\beta_t = \sqrt{1 - \alpha_t^2}$,相应地有
\begin{equation}\small{p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \approx p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) = \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \frac{\beta_t^2}{\bar{\beta}_t}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right),\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)}\label{eq:choice-1}\end{equation}
这就是上一篇文章所推导的DDPM。特别是,DDIM论文中还对$\sigma_t = \eta\frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}$做了对比实验,其中$\eta\in[0, 1]$。
第二个例子就是取$\sigma_t = \beta_t$,这也是前两篇文章所指出的$\sigma_t$的两个选择之一,在此选择下式$\eqref{eq:p-xt-x0-2}$未能做进一步的化简,但DDIM的实验结果显示此选择在DDPM的标准参数设置下表现还是很好的。
最特殊的一个例子是取$\sigma_t = 0$,此时从$\boldsymbol{x}_t$到$\boldsymbol{x}_{t-1}$是一个确定性变换
\begin{equation}\boldsymbol{x}_{t-1} = \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \left(\bar{\beta}_t - \alpha_t \bar{\beta}_{t-1}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right)\label{eq:sigma=0}\end{equation}
这也是DDIM论文中特别关心的一个例子,准确来说,原论文的DDIM就是特指$\sigma_t=0$的情形,其中“I”的含义就是“Implicit”,意思这是一个隐式的概率模型,因为跟其他选择所不同的是,此时从给定的$\boldsymbol{x}_T = \boldsymbol{z}$出发,得到的生成结果$\boldsymbol{x}_0$是不带随机性的。后面我们将会看到,这在理论上和实用上都带来了一些好处。
加速生成 #
值得指出的是,在这篇文章中我们没有以$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$为出发点,所以前面的所有结果实际上全都是以$\bar{\alpha}_t,\bar{\beta}_t$相关记号给出的,而$\alpha_t,\beta_t$则是通过$\alpha_t=\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}$和$\beta_t = \sqrt{1 - \alpha_t^2}$派生出来的记号。从损失函数$\left\Vert\boldsymbol{\varepsilon} - \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}, t)\right\Vert^2$可以看出,给定了各个$\bar{\alpha}_t$,训练过程也就确定了。
从这个过程中,DDIM进一步留意到了如下事实:
高观点2: DDPM的训练结果实质上包含了它的任意子序列参数的训练结果。
具体来说,设$\boldsymbol{\tau} = [\tau_1,\tau_2,\dots,\tau_{\dim(\boldsymbol{\tau})}]$是$[1,2,\cdots,T]$的任意子序列,那么我们以$\bar{\alpha}_{\tau_1},\bar{\alpha}_{\tau_2},\cdots,\bar{\alpha}_{\dim(\boldsymbol{\tau})}$为参数训练一个扩散步数为$\dim(\boldsymbol{\tau})$步的DDPM,其目标函数实际上是原来以$\bar{\alpha}_1,\bar{\alpha}_2,\cdots,\bar{\alpha}_T$的$T$步DDPM的目标函数的一个子集!所以在模型拟合能力足够好的情况下,它其实包含了任意子序列参数的训练结果。
那么反过来想,如果有一个训练好的$T$步DDPM模型,我们也可以将它当成是以$\bar{\alpha}_{\tau_1},\bar{\alpha}_{\tau_2},\cdots,\bar{\alpha}_{\dim(\boldsymbol{\tau})}$为参数训练出来的$\dim(\boldsymbol{\tau})$步模型,而既然是$\dim(\boldsymbol{\tau})$步的模型,生成过程也就只需要$\dim(\boldsymbol{\tau})$步了,根据式$\eqref{eq:p-xt-x0-2}$有:
\begin{equation}p(\boldsymbol{x}_{\tau_{i-1}}|\boldsymbol{x}_{\tau_i}) \approx \mathcal{N}\left(\boldsymbol{x}_{\tau_{i-1}}; \frac{\bar{\alpha}_{\tau_{i-1}}}{\bar{\alpha}_{\tau_i}}\left(\boldsymbol{x}_{\tau_i} - \left(\bar{\beta}_{\tau_i} - \frac{\bar{\alpha}_{\tau_i}}{\bar{\alpha}_{\tau_{i-1}}}\sqrt{\bar{\beta}_{\tau_{i-1}}^2 - \tilde{\sigma}_{\tau_i}^2}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_{\tau_i}, \tau_i)\right), \tilde{\sigma}_{\tau_i}^2 \boldsymbol{I}\right)\end{equation}
这就是加速采样的生成过程了,从原来的$T$步扩散生成变成了$\dim(\boldsymbol{\tau})$步。要注意不能直接将式$\eqref{eq:p-xt-x0-2}$的$\alpha_t$换成$\alpha_{\tau_i}$,因为我们说过$\alpha_t$是派生记号而已,它实际上等于$\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}$,因此$\alpha_t$要换成$\frac{\bar{\alpha}_{\tau_i}}{\bar{\alpha}_{\tau_{i-1}}}$才对。同理,$\tilde{\sigma}_{\tau_i}$也不是直接取$\sigma_{\tau_i}$,而是在将其定义全部转化为$\bar{\alpha},\bar{\beta}$符号后,将$t$替换为$\tau_i$、$t-1$替换为$\tau_{i-1}$,比如式$\eqref{eq:choice-1}$对应的$\tilde{\sigma}_{\tau_i}$为
\begin{equation}\sigma_t = \frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}=\frac{\bar{\beta}_{t-1}}{\bar{\beta}_t}\sqrt{1 - \frac{\bar{\alpha}_t^2}{\bar{\alpha}_{t-1}^2}}\quad\to\quad\frac{\bar{\beta}_{\tau_{i-1}}}{\bar{\beta}_{\tau_i}}\sqrt{1 - \frac{\bar{\alpha}_{\tau_i}^2}{\bar{\alpha}_{\tau_{i-1}}^2}}=\tilde{\sigma}_{\tau_i}\end{equation}
可能读者又想问,我们为什么干脆不直接训练一个$\dim(\boldsymbol{\tau})$步的扩散模型,而是要先训练$T > \dim(\boldsymbol{\tau})$步然后去做子序列采样?笔者认为可能有两方面的考虑:一方面从$\dim(\boldsymbol{\tau})$步生成来说,训练更多步数的模型也许能增强泛化能力;另一方面,通过子序列$\boldsymbol{\tau}$进行加速只是其中一种加速手段,训练更充分的$T$步允许我们尝试更多的其他加速手段,但并不会显著增加训练成本。
实验结果 #
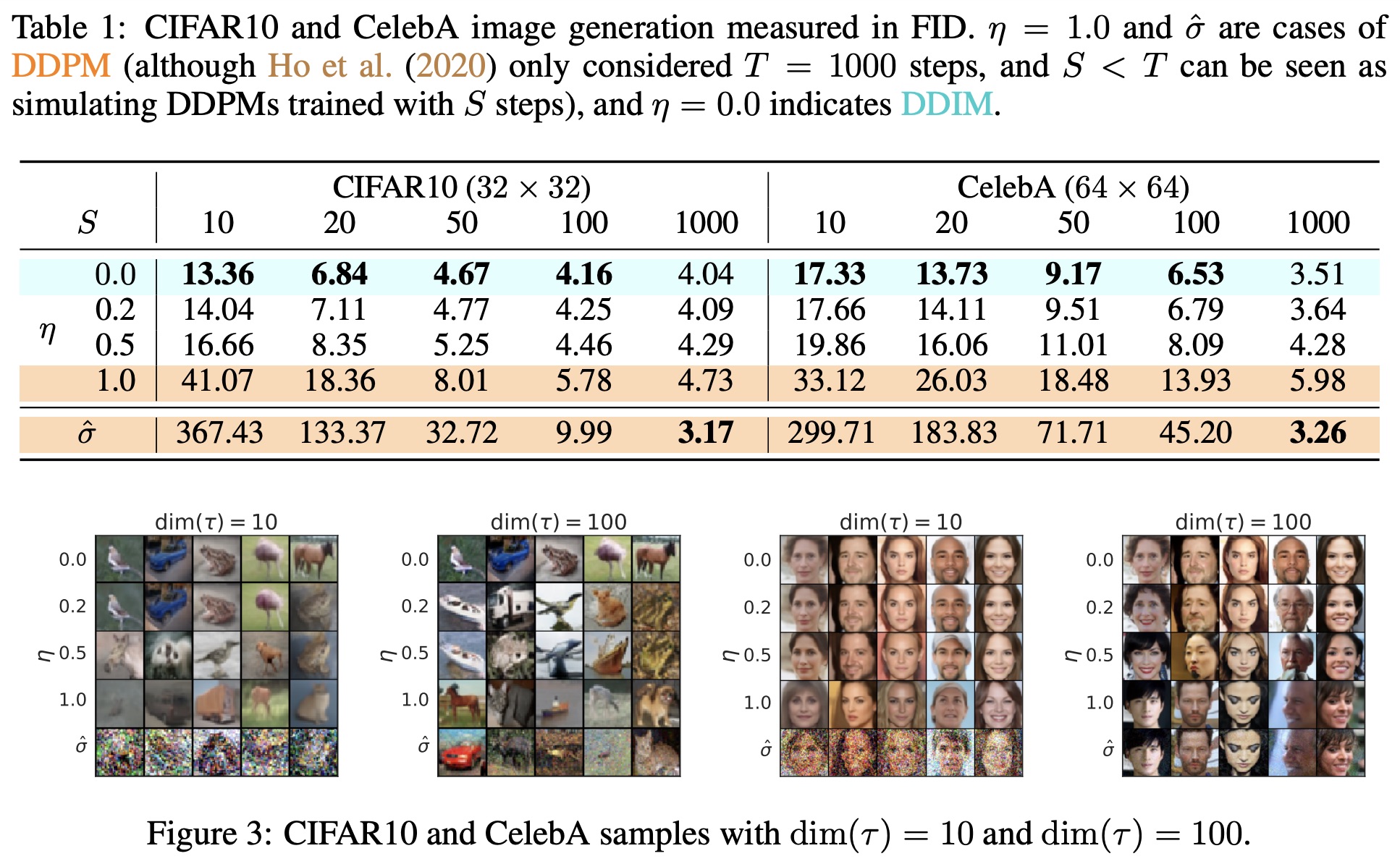
原论文对不同的噪声强度和扩散步数$\dim(\boldsymbol{\tau})$做了组合对比,大致上的结果是“噪声越小,加速后的生成效果越好”,如下图
笔者的参考实现如下:
个人的实验结论是:
1、可能跟直觉相反,生成过程中的$\sigma_t$越小,最终生成图像的噪声和多样性反而相对来说越大;
2、扩散步数$\dim(\boldsymbol{\tau})$越少,生成的图片更加平滑,多样性也会有所降低;
3、结合1、2两点得知,在扩散步数$\dim(\boldsymbol{\tau})$减少时,可以适当缩小$\sigma_t$,以保持生成图片质量大致不变,这跟DDIM原论文的实验结论是一致的;
4、在$\sigma_t$较小时,相比可训练的Embedding层,用固定的Sinusoidal编码来表示$t$所生成图片的噪声要更小;
5、在$\sigma_t$较小时,原论文的U-Net架构(Github中的ddpm2.py)要比笔者自行构思的U-Net架构(Github中的ddpm.py)所生成图片的噪声要更小;
6、但个人感觉,总体来说不带噪声的生成过程的生成效果不如带噪声的生成过程,不带噪声时生成效果受模型架构影响较大。
此外,对于$\sigma_t=0$时的DDIM,它就是将任意正态噪声向量变换为图片的一个确定性变换,这已经跟GAN几乎一致了,所以跟GAN类似,我们可以对噪声向量进行插值,然后观察对应的生成效果。但要注意的是,DDPM或DDIM对噪声分布都比较敏感,所以我们不能用线性插值而要用球面插值,因为由正态分布的叠加性,如果$\boldsymbol{z}_1,\boldsymbol{z}_2\sim\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$,$\lambda\boldsymbol{z}_1 + (1-\lambda)\boldsymbol{z}_2$一般就不服从$\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$,要改为
\begin{equation}\boldsymbol{z} = \boldsymbol{z}_1 \cos\frac{\lambda\pi}{2} + \boldsymbol{z}_2 \sin\frac{\lambda\pi}{2},\quad \lambda\in[0, 1]\end{equation}
插值效果演示(笔者自己训练的模型):
微分方程 #
最后,我们来重点分析一下$\sigma_t = 0$的情形。此时$\eqref{eq:sigma=0}$可以等价地改写成:
\begin{equation}\frac{\boldsymbol{x}_t}{\bar{\alpha}_t} - \frac{\boldsymbol{x}_{t-1}}{\bar{\alpha}_{t-1}} = \left(\frac{\bar{\beta}_t}{\bar{\alpha}_t} - \frac{\bar{\beta}_{t-1}}{\bar{\alpha}_{t-1}}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\end{equation}
当$T$足够大,或者说$\alpha_t$与$\alpha_{t-1}$足够小时,我们可以将上式视为某个常微分方程的差分形式。特别地,引入虚拟的时间参数$s$,我们得到
\begin{equation}\frac{d}{ds}\left(\frac{\boldsymbol{x}(s)}{\bar{\alpha}(s)}\right) = \boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\boldsymbol{x}(s), t(s)\right)\frac{d}{ds}\left(\frac{\bar{\beta}(s)}{\bar{\alpha}(s)}\right)\label{eq:ode}\end{equation}
不失一般性,假设$s\in[0,1]$,其中$s=0$对应$t=0$、$s=1$对应$t=T$。注意DDIM原论文直接用$\frac{\bar{\beta}(s)}{\bar{\alpha}(s)}$作为虚拟时间参数,这原则上是不大适合的,因为它的范围是$[0,\infty)$,无界的区间不利于数值求解。
那么现在我们要做的事情就是在给定$\boldsymbol{x}(1)\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$的情况下,去求解出$\boldsymbol{x}(0)$。而DDPM或者DDIM的迭代过程,对应于该常微分方程的欧拉方法。众所周知欧拉法的效率相对来说是最慢的,如果要想加速求解,可以用Heun方法、R-K方法等。也就是说,将生成过程等同于求解常微分方程后,可以借助常微分方程的数值解法,为生成过程的加速提供更丰富多样的手段。
以DDPM的默认参数$T=1000$、$\alpha_t = \sqrt{1 - \frac{0.02t}{T}}$为例,我们重复《生成扩散模型漫谈(一):DDPM = 拆楼 + 建楼》所做的估计
\begin{equation}\log \bar{\alpha}_t = \sum_{i=k}^t \log\alpha_k = \frac{1}{2} \sum_{k=1}^t \log\left(1 - \frac{0.02k}{T}\right) < \frac{1}{2} \sum_{k=1}^t \left(- \frac{0.02k}{T}\right) = -\frac{0.005t(t+1)}{T}\end{equation}
事实上,由于每个$\alpha_k$都很接近于1,所以上述估计其实也是一个很好的近似。而我们说了本文的出发点是$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$,所以应该以$\bar{\alpha}_t$为起点,根据上述近似,我们可以直接简单地取
\begin{equation}\bar{\alpha}_t = \exp\left(-\frac{0.005t^2}{T}\right) = \exp\left(-\frac{5t^2}{T^2}\right)\end{equation}
如果取$s=t/T$为参数,那么正好$s\in[0,1]$,此时$\bar{\alpha}(s)=e^{-5s^2}$,代入到式$\eqref{eq:ode}$化简得
\begin{equation}\frac{d\boldsymbol{x}(s)}{ds} = 10s\left(\frac{\boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\boldsymbol{x}(s), sT\right)}{\sqrt{1-e^{-10s^2}}} - \boldsymbol{x}(s)\right)\end{equation}
也可以取$s=t^2/T^2$为参数,此时也有$s\in[0,1]$,以及$\bar{\alpha}(s)=e^{-5s}$,代入到式$\eqref{eq:ode}$化简得
\begin{equation}\frac{d\boldsymbol{x}(s)}{ds} = 5\left(\frac{\boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\boldsymbol{x}(s), \sqrt{s}T\right)}{\sqrt{1-e^{-10s}}} - \boldsymbol{x}(s)\right)\end{equation}
文章小结 #
本文接着上一篇DDPM的推导思路来介绍了DDIM,它重新审视了DDPM的出发点,去掉了推导过程中的$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$,从而获得了一簇更广泛的解和加速生成过程的思路,最后这簇新解还允许我们将生成过程跟常微分方程的求解联系起来,从而借助常微分方程的方法进一步对生成过程进行研究。
转载到请包括本文地址:https://spaces.ac.cn/archives/9181
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jul. 27, 2022). 《生成扩散模型漫谈(四):DDIM = 高观点DDPM 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/9181
@online{kexuefm-9181,
title={生成扩散模型漫谈(四):DDIM = 高观点DDPM},
author={苏剑林},
year={2022},
month={Jul},
url={\url{https://spaces.ac.cn/archives/9181}},
}











September 1st, 2022
(5)成立是因为,要想让(3)成立,表格里第一行和第四行的对应项系数相等。
September 24th, 2022
欸,为什么ddim的子序列加速效果能够好过ddpm的子序列加速效果呀
DDIM的$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$对$\boldsymbol{x}_0$的依赖最小,也就是说,逐渐地它越来越不依赖于预估的、可能有误差的$\boldsymbol{x}_0$,减少了累积误差。
补充一个原作者的解释,采样过程中DDIM对应的noise更小。
https://github.com/ermongroup/ddim/issues/8
是不是也可以这么理解:
1. DDIM这种训练时估$x_{0}^{/prime}$
2. sample的时候借助于“预估-修正”机理,$x_{0}^{/prime}$就越来越好
DDPM跟DDIM训练过程是一样的,模型相互之间通用。
感谢提供的作者GITHUB,不过虽然但是,你给的这个链接里并不是回答这个问题的,是回答cases of eta=1 and hat{sigma} 有什么不同,不同点在于用的误差一个假设X0是德尔塔分布一个假设是高斯分布。
但是为什么hat{sigma}这个在高步数(1000)的表现的最好,这确实奇怪,因为用hat{sigma}反而是不符合公式的。
对不起不是德尔塔是狄拉克分布,太久没用忘了名字。。。。
这个问题,可能从SDE角度来回答才能比较准确~
苏老师,这里我有点疑惑,从哪里可以得出“DDIM的p(xt−1|xt,x0)对x0的依赖最小”这个结论的?是因为和DDPM相比,其采样次数更少吗?还是别的什么原因
根据$\eqref{eq:p-xt-x0}$,$\boldsymbol{x}_0$的系数
$$\bar{\alpha}_{t-1} - \frac{\bar{\alpha}_t\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t}$$
最小值在$\sigma_t=0$时取到。
September 24th, 2022
苏老师,为什么$\int p(x_{t-1}|x_t,x_0)p(x_t|x_0)dx_t$对应的采样方式是表格里的形式呢?这里该咋理解呢
为什么不是呢?那里不能理解呢?
看到表格中对应的采样方式,我自己的理解是先从$x_0$出发,通过$p(x_t|x_0)$得到$x_t$,再从$x_t,x_0$出发,通过$p(x_{t-1}|x_t,x_0)$来得到$x_{t-1}$,简而言之像是从$p(x_{t-1}|x_t,x_0)p(x_t|x_0)$这个联合分布中采得的样本。剩下的对于$x_t$的积分对应在采样方式中的哪一部分呢?将$x_t$通过$x_0$来表示出来就代表利用积分消掉了吗?
你都说“再从$\boldsymbol{x}_t, \boldsymbol{x}_0$出发,得到$\boldsymbol{x}_{t-1}$”了,如果我只考虑$\boldsymbol{x}_{t-1}$,那么就对应一个一元分布啊,一元分布的概率密度函数,怎么可能是二元的$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) p(\boldsymbol{x}_t|\boldsymbol{x}_0)$呢?
不过你的理解其实很接近答案了。其实是这样采样出来的二元组$(\boldsymbol{x}_t, \boldsymbol{x}_{t-1})$服从联合分布$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) p(\boldsymbol{x}_t|\boldsymbol{x}_0)$,而如果只考虑$\boldsymbol{x}_{t-1}$的话,那就是在考虑边缘分布,联合分布的边缘分布,不就是对另一个变量积分吗?所以$\boldsymbol{x}_{t-1}$的边缘分布就是$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) p(\boldsymbol{x}_t|\boldsymbol{x}_0)$对$\boldsymbol{x}_t$的积分。
啊!明白了!谢谢苏老师!
工作多年,数学都忘光了。所以请教下,(3)式是不是无条件成立的公式?表格最后一行,采样指的就是满足(3)式左边公式的采样,其分布根据(3)式,必须等于(3)式右边公式,于是推出(5)式?
初一看压根没看出(3)式有啥用。因为作为文盲,看到表格最后一行的采样公式,很自然地认为就是简单的公式代入,自然而然导出(5)式,和(3)式看起来没啥关系。
细想一样,感觉可能这种采样符合了(3)式左边的分布,根据(3)式等于右边的分布,所以才有(5)式,而不是简单的代入法。
可以这么理解,$(3)$的左边就是其右边的定义,所以两者必然相等。
不考虑(3),表格最后一行一开始就不成立啊?你怎么代入能代入出这个关系呢
October 6th, 2022
为什么公式(7)不需要限定-α和-β的平方相加等于1?
严格来讲扩散模型包括DDPM就不一定要限定$\alpha^2+\beta^2=1$。
October 7th, 2022
我发现采用 IDDPM 和 DDPM beats GANs 论文中的 respaced sampling 技巧,用 50, 100, 250 steps 取得的效果就很好了,好像比 DDIM 的加速采样还要好。
请问你是自己做实验看的吗?
我感觉这三个文章用的不都是子序列采样吗,只是采样时候噪声项不同,误差不一样而已?
对,我自己做的实验
感觉没什么区别。
October 10th, 2022
苏神,关于 DDIM 加速生成的这段话,我还是不太理解,可否解答一下。
设τ=[τ1,τ2,…,τdim(τ)]是[1,2,⋯,T]的任意子序列,那么我们以α¯τ1,α¯τ2,⋯,α¯dim(τ)为参数训练一个扩散步数为dim(τ)步的DDPM,其目标函数实际上是原来以α¯1,α¯2,⋯,α¯T的T步DDPM的目标函数的一个子集!所以在模型拟合能力足够好的情况下,它其实包含了任意子序列参数的训练结果。
如果给定的模型是在 T=1000 的条件下训练好的,那模型学会的应该是 p(x_1000|x_999).etc,现在给个均匀间隔的子序列 S=100 来采样,模型预测的是 p(x_1000|x_990) 么? 如果是的话,原模型压根就没见过输入是 x_1000,输出是 x_990 的情况诶
别忘了DDIM视角下,训练目标只是$\boldsymbol{x}_t$预测$\boldsymbol{x}_0$,假如你训练了$\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_{1000}$来预测$\boldsymbol{x}_0$的模型,那么自然也相当于训练了单纯的$\boldsymbol{x}_{10},\boldsymbol{x}_{20},\cdots,\boldsymbol{x}_{1000}$来预测$\boldsymbol{x}_0$的模型。
多谢苏神的回复,现在很清晰了:D
最开始的输入$x_{1000}$是高斯噪声,经过一次采样不是只能得到$x_{999}$吗?那怎加速得到$x_{500}$呢?
以DDIM为例,有
$$\boldsymbol{x}_{t-1} = \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \left(\bar{\beta}_t - \alpha_t \bar{\beta}_{t-1}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right) = \frac{\bar{\alpha}_{t-1}}{\bar{\alpha}_t}\left(\boldsymbol{x}_t - \left(\bar{\beta}_t - \frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}} \bar{\beta}_{t-1}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right)$$
如果你把$\bar{\alpha}_{t-1},\bar{\beta}_{t-1}$都换成$\bar{\alpha}_{t-100},\bar{\beta}_{t-100}$,那么$\boldsymbol{x}_{1000}$的下一步就可以认为是$\boldsymbol{x}_{900}$了。
November 10th, 2022
苏神,为啥 DDPM 原版的模型做确定性生成 (sigma=0)的话,图片质量就很差很差呢,基本上是纯黑的图片
因为$\eqref{eq:margin}$是$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$的一个必要条件,直接在原始DDPM中取采样方差为0,不满足式$\eqref{eq:margin}$。
想请问一下,DDPM原文中令$\sigma_t=\beta_t$是不是也是不满足式子(3)的,那为什么那样是可以采样生成的呢?是不是因为$\frac{\bar\beta_{t-1}}{\bar\beta_{t}}$在T很大的情况下接近于1,所以在两个极端$\sigma_t=\beta_t$和$\sigma_t=\beta_t\frac{\bar\beta_{t-1}}{\bar\beta_{t}}$之间取方差还是近似满足式子(3)的,而直接让方差为0就差的很远了。
DDPM的$\sigma_t$是$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$的标准差,不是$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$的标准差,事实上两者有一定差距。直接令$\sigma_t=\beta_t$也可行,说明DDPM对采样标准差的选取有一定的容错性。
更准确的标准差估计,可以参考:https://kexue.fm/archives/9245
November 12th, 2022
文中说“当$T$足够大,或者说$\alpha_t$与$\alpha_{t−1}$足够小时,我们可以将上式视为某个常微分方程的差分形式”。请问这里怎么理解,为什么需要$\alpha_t$与$\alpha_{t−1}$足够小才能视为常微分方程的差分形式呢?
我理解应该是需要$t\rightarrow 0$,即$x_t=\bar{\alpha}_tx_0+\bar{\beta}_t\varepsilon_1\rightarrow x_0$。
感谢苏神~
用微分近似差分,本就是无限小距离内才成立(切线近似割线)。
November 22nd, 2022
请问为什么DDIM是确定性采样,但反而实验效果会展现多样性更好呢?这个点不太好直观理解,希望能得到苏老师的解答!
确定性采样是指从$\boldsymbol{x}_T$到$\boldsymbol{x}_0$的变换是确定性的,但是$\boldsymbol{x}_T$本身就是随机的。$\boldsymbol{x}_T$服从跟训练数据同样维度的多元标准正态分布,而事实上训练数据很可能只是高维空间中的一个子流形,因此即便是确定性变换,理论上也有足够能力可以保证生成数据的多样性(好比“立体”映射到“平面”,总能构造一个满射出来)
你这问题问得太好了我也想问,苏神的回答有点没看懂,苏神说从“立体”映射到“平面”,但从$\boldsymbol{x}_T$到$\boldsymbol{x}_0$是同维度映射,训练集更像是分布在此维空间的点,然后训练是向着点聚类,这是我目前的直观感受,也会继续学习如果看到能看得懂的全面的解答会回来贴上回复
图片集更接近一个低维空间的子流形,所以图片才是面,随机噪声是体。
我也有这个疑问,我了解苏神意思,就是确定性采样也能保证多样性。
但是按照苏神的实验结论,为什么方差越小,反而多样性越好还是个问题(悄悄问一句,苏神这个对多样性的判断是肉眼看的嘛?)。
这是不是也能反向印证一个事实:diffusion model的多样性主要来源于$x_T$的随机采样生成,采样过程中所加的随机噪声对多样性的作用不大,反而更多的起到对u-net早期错误的修正作用(所以diffusion SDE 的效果一般要好于diffusion ODE)。
而且,采样步数越小,图像越平滑,多样性越差,是因为步数少,没有生成一些细节吗?希望苏神能一起讨论一下,感谢!
1、我自己关于多样性的判断是肉眼看的;
2、主要来源肯定是$x_T$,理论上迭代过程中的噪声带来的是细节;
3、采样步数越少,缺少的也是细节。
December 2nd, 2022
苏老师好!想请教一下,微分方程那一小节中,"当T足够大,或者说$\alpha_t$与$\alpha_{t-1}$足够小时,我们可以将上式视为某个常微分方程的差分形式"是为什么?为什么要满足T足够大或者$\alpha_t$与$\alpha_{t-1}$足够小的条件才能将公式(16)视为常微分方程的差分形式?
足够小的区间内,才能将曲线近似为直线。
因为要把$\Delta y$给变成$dy$,再在两边同时除$ds$。