CoSENT(一):比Sentence-BERT更有效的句向量方案
By 苏剑林 | 2022-01-06 | 366825位读者 |学习句向量的方案大致上可以分为无监督和有监督两大类,其中有监督句向量比较主流的方案是Facebook提出的“InferSent”,而后的“Sentence-BERT”进一步在BERT上肯定了它的有效性。然而,不管是InferSent还是Sentence-BERT,它们在理论上依然相当令人迷惑,因为它们虽然有效,但存在训练和预测不一致的问题,而如果直接优化预测目标cos值,效果往往特别差。
最近,笔者再次思考了这个问题,经过近一周的分析和实验,大致上确定了InferSent有效以及直接优化cos值无效的原因,并提出了一个优化cos值的新方案CoSENT(Cosine Sentence)。实验显示,CoSENT在收敛速度和最终效果上普遍都比InferSent和Sentence-BERT要好。
朴素思路 #
本文的场景是利用文本匹配的标注数据来构建句向量模型,其中所利用到的标注数据是常见的句子对样本,即每条样本是“(句子1, 句子2, 标签)”的格式,它们又大致上可以分类“是非类型”、“NLI类型”、“打分类型”三种,参考《用开源的人工标注数据来增强RoFormer-Sim》中的“分门别类”一节。
失效的Cos #
简单起见,我们可以先只考虑“是非类型”的数据,即“(句子1, 句子2, 是否相似)”的样本。假设两个句子经过编码模型后分别得到向量$u,v$,由于检索阶段计算的是余弦相似度$\cos(u,v)=\frac{\langle u,v\rangle}{\Vert u\Vert \Vert v\Vert}$,所以比较自然的想法是设计基于$\cos(u,v)$的损失函数,比如
\begin{align}t\cdot (1 - \cos(u, v)) + (1 - t) \cdot (1 + \cos(u,v))\label{eq:cos-1}\\
t\cdot (1 - \cos(u, v))^2 + (1 - t) \cdot \cos^2(u,v)\label{eq:cos-2}
\end{align}
其中$t\in\{0,1\}$表示是否相似。类似的loss还可以写出很多,大致的意思都是让正样本对的相似度尽可能大、负样本对的相似度尽可能小。然而,直接优化这些目标的实验结果往往特别差(至少明显比InferSent要差),在某些情况下甚至还不如随机初始化的效果。
难搞的阈值 #
这是因为,通常文本匹配语料中标注出来的负样本对都是“困难样本”,常见的是语义不相同但字面上有比较多的重合。此时,如果我们用式$\eqref{eq:cos-1}$作为损失函数,那么正样本对的目标是1、负样本对的目标是-1,如果我们用式$\eqref{eq:cos-2}$作为损失函数,那么正样本对的目标是1、负样本对的目标是0。不管哪一种,负样本对的目标都“过低”了,因为对于“困难样本”来说,虽然语义不同,但依然是“相似”,相似度不至于0甚至-1那么低,如果强行让它们往0、-1学,那么通常的后果就是造成过度学习,从而失去了泛化能力,又或者是优化过于困难,导致根本学不动。
要验证这个结论很简单,只需要把训练集的负样本换成随机采样的样本对(视作更弱的负样本对),然后用上述loss进行训练,就会发现效果反而会变好。如果不改变负样本对,那么缓解这个问题的一个方法是给负样本对设置更高的阈值,比如
\begin{equation}t\cdot (1 - \cos(u, v)) + (1 - t) \cdot \max(\cos(u,v),0.7)\end{equation}
这样一来,负样本对的相似度只要低于0.7就不优化了,从而就不那么容易过度学习了。但这仅仅是缓解,效果也很难达到最优,而且如何选取这个阈值依然是比较困难的问题。
InferSent #
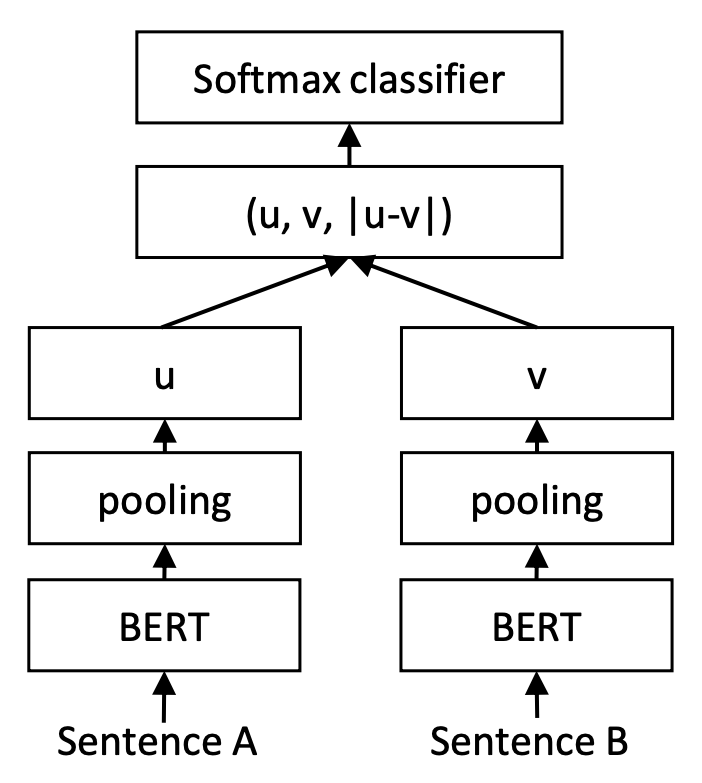
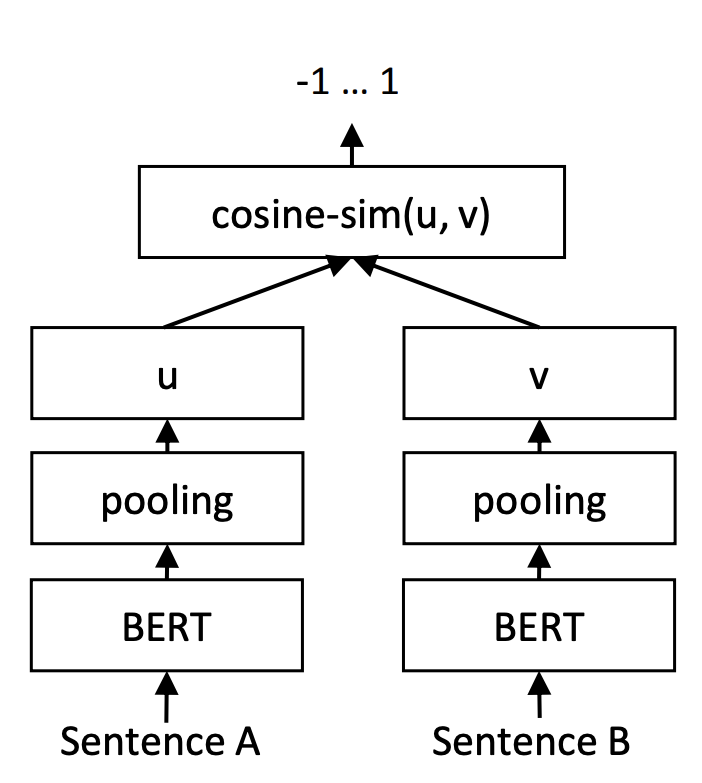
让人倍感神奇的是,训练和预测不一致的InferSent和Sentence-BERT,却在这个问题上表现良好。以Sentence-BERT为例,它的训练阶段是将$u,v,|u−v|$(其中$|u−v|$是指$u−v$的每个元素都取绝对值后构成的向量)拼接起来做为特征,后面接一个全连接层做2分类(如果是NLI数据集则是3分类),而在预测阶段,还是跟普通的句向量模型一样,先计算句向量然后算cos值作为相似度。如下图所示:
再闭门造车 #
为什么InferSent和Sentence-BERT会有效?在《用开源的人工标注数据来增强RoFormer-Sim》中的“闭门造车”一节笔者给出了一个基于容错性的解释,而经过这段时间的思考,笔者对这个问题有了一个新的理解,这里再跟大家分享交流一下。
一般情况下,哪怕负样本对是“困难样本”,总体而言正样本对的字面相似度是大于负样本对的,这样一来,哪怕是对于初始模型,正样本对的差距$\Vert u-v\Vert$总体较小,而负样本对的差距$\Vert u-v\Vert$总体较大,我们可以想象正样本对的$u-v$主要分布在一个半径较小的球面附近,而负样本对的$u-v$分布在一个半径较大的球面附近,也就是说,初始阶段$u-v$本身就有聚类倾向,我们接下来只需要根据标签信息强化这种聚类倾向,使得正样本对的$u-v$依然保持更小,负样本对的$u-v$保持更大。一个直接的做法就是$u-v$后面接一个Dense分类器,然而常规的分类器是基于内积的,它没法区分两个分布在不同球面的类别,所以我们加上绝对值变成$|u-v|$,将球面变为局部的球盖(或者说将球体变成锥形),此时就可以用Dense分类层来分类了。这就是笔者认为的$|u-v|$的来源。
至于$u,v$的拼接,笔者认为是用来消除各向异性的。像“BERT+[CLS]”的句向量模型,在初始阶段具有严重的各向异性,这种各向异性对句向量的效果有着比较严重的负面影响,而$|u-v|$只是向量的相对差距,无法明显改善这种各向异性。而$u,v$拼接之后接Dense层,由于Dense层的类别向量是随机初始化的,所以相当于给了$u,v$一个随机的优化方向,迫使它们各自“散开”,远离当前的各向异性状态。
潜在的问题 #
InferSent和Sentence-BERT虽然有效,但也存在比较明显的问题。
比如,前面说了它有效的原因是初始阶段就有聚类倾向,而标签训练只是强化这个聚类倾向信息,所以“初始阶段就有聚类倾向”就显得相当重要,它意味着其效果比较依赖于初始模型,比如“BERT+平均池化”的最终效果就优于“BERT+[CLS]”,因为前者在初始阶段的区分度就更好。
此外,InferSent和Sentence-BERT终究是训练和预测不一致的方案,所以存在一定的概率会“训崩”,具体表现为训练loss还在下降,训练acc还在提升,但是基于余弦值的评测指标(如Spearman系数)却明显下降,哪怕是训练集也是如此。这说明训练还是正常进行的,但是已经脱离了“正样本对的$u-v$更小、负样本对的$u-v$更大”的分类依据,从而余弦值就崩了。
InferSent和Sentence-BERT还存在调优困难问题,这同样是因为训练和预测的不一致性,导致我们很难确定对哪些训练过程的调整会给预测结果带来正面帮助。
CoSENT #
简单来说,就是InferSent和Sentence-BERT算是一种可用的方案,但存在诸多的不确定性。那难道优化cos值就真的没有出头之日了吗?当然不是。早前的SimCSE其实也有一个有监督版,它也是直接优化cos值,但它要用到“(原始句子, 相似句子, 不相似句子)”格式的三元组数据。而本文提出的CoSENT,则进一步改进了上述思路,使得训练过程只用到句子对样本。
新损失函数 #
我们记$\Omega_{pos}$为所有的正样本对集合,$\Omega_{neg}$为所有的负样本对集合,其实我们是希望对于任意的正样本对$(i,j)\in \Omega_{pos}$和负样本对$(k,l)\in \Omega_{neg}$,都有
\begin{equation}\cos(u_i,u_j) > \cos(u_k, u_l)\end{equation}
其实$u_i,u_j,u_k,u_l$是它们各自的句向量。说白了,我们只希望正样本对的相似度大于负样本对的相似度,至于大多少,模型自己决定就好。事实上语义相似度常见的评价指标spearman也是一样,它只依赖于预测结果的相对顺序,而不依赖于具体的值。
在《将“Softmax+交叉熵”推广到多标签分类问题》中,我们介绍了处理这类需求的一个有效方案,那就是Circle Loss理论里边的公式(1):
\begin{equation}\log \left(1 + \sum\limits_{i\in\Omega_{neg},j\in\Omega_{pos}} e^{s_i-s_j}\right)\end{equation}
简单来说,就是如果你希望最终实现$s_i < s_j$,那么就往$\log$里边加入$e^{s_i-s_j}$一项。对应我们这里的场景,我们可以得到损失函数
\begin{equation}\log \left(1 + \sum\limits_{(i,j)\in\Omega_{pos},(k,l)\in\Omega_{neg}} e^{\lambda(\cos(u_k, u_l) - \cos(u_i, u_j))}\right)\label{eq:cosent}\end{equation}
其中$\lambda > 0$是一个超参数,本文后面的实验取了20。这就是CoSENT的核心内容了,它是一个优化cos值的新的损失函数。
通用的排序 #
可能有读者质疑:就算这里的式$\eqref{eq:cosent}$真的可用,那也只适用于二分类数据,像NLI数据是3分类的就不能用了?
事实上,式$\eqref{eq:cosent}$本质上是一个为排序设计的损失函数,它可以更加通用地写成:
\begin{equation}\log \left(1 + \sum\limits_{\text{sim}(i,j) \gt \text{sim}(k,l)} e^{\lambda(\cos(u_k, u_l) - \cos(u_i, u_j))}\right)\label{eq:cosent-2}\end{equation}
也就是说,只要我们认为样本对$(i,j)$的真实相似度应该大于$(k,l)$的真实相似度,就可以往$\log$里边加入$e^{\lambda(\cos(u_k, u_l) - \cos(u_i, u_j))}$;换句话说,只要我们能够为样本对设计顺序,那么就可以用式$\eqref{eq:cosent-2}$
对于NLI数据而言,它有“蕴含”、“中立”、“矛盾”三种标签,我们自然可以认为两个“蕴含”的句子相似度大于两个“中立”的句子,而两个“中立”的句子相似度大于两个“矛盾”的句子,这样基于这三种标签就可以为NLI的句子对排序了。而有了这个排序后,NLI数据也可以用CoSENT来训练了。类似地,对于STS-B这种本身就是打分的数据,就更适用于CoSENT了,因为打分标签本身就是排序信息。
当然,如果多类别之间没有这种序关系,那就不能用CoSENT了。然而,对于无法构建序关系的多类别句子对数据,InferSent和Sentence-BERT能否出合理的句向量模型,笔者也是持怀疑态度。目前没看到类似的数据集,也就无从验证了。
优秀的效果 #
笔者在多个中文数据集上对CoSENT进行了实验,分别比较了在原有训练集上训练以及在NLI数据集训练两种方案,大多数实验结果都表明CoSENT明显优于Sentence-BERT。测试数据集同《无监督语义相似度哪家强?我们做了个比较全面的评测》,每个数据集都被划分为train、valid、test三部分,评测指标是预测值和标签的spearman系数。
下面是用各自的train集进行训练后,test集的效果:
\begin{array}{c|ccccc|c}
\hline
& \text{ATEC} & \text{BQ} & \text{LCQMC} & \text{PAWSX} & \text{STS-B} & \text{Avg}\\
\hline
\text{BERT+CoSENT} & \textbf{49.74} & \textbf{72.38} & 78.69 & \textbf{60.00} & \textbf{80.14} & \textbf{68.19}\\
\text{Sentence-BERT} & 46.36 & 70.36 & \textbf{78.72} & 46.86 & 66.41 & 61.74\\
\hline
\text{RoBERTa+CoSENT} & \textbf{50.81} & \textbf{71.45} & \textbf{79.31} & \textbf{61.56} & \textbf{81.13}
& \textbf{68.85}\\
\text{Sentence-RoBERTa} & 48.29 & 69.99 & 79.22 & 44.10 & 72.42 & 62.80\\
\hline
\end{array}
下面则是用开源的NLI数据作为训练集进行训练后,每个任务的test集的效果:
\begin{array}{c|ccccc|c}
\hline
& \text{ATEC} & \text{BQ} & \text{LCQMC} & \text{PAWSX} & \text{STS-B} & \text{Avg}\\
\hline
\text{BERT+CoSENT} & \textbf{28.93} & 41.84 & \textbf{66.07} & \textbf{20.49} & 73.91 & \textbf{46.25} \\
\text{Sentence-BERT} & 28.19 & \textbf{42.73} & 64.98 & 15.38 & \textbf{74.88} & 45.23 \\
\hline
\text{RoBERTa+CoSENT} & 31.84 & \textbf{46.65} & \textbf{68.43} & \textbf{20.89} & \textbf{74.37} & \textbf{48.43}\\
\text{Sentence-RoBERTa} & \textbf{31.87} & 45.60 & 67.89 & 15.64 & 73.93 & 46.99\\
\hline
\end{array}
可以看到,大多数任务上CoSENT都有较为明显的提升,而个别有任务上的下降也是比较小的(1%以内),原生训练的平均提升幅度超过6%,而NLI训练的平均提升幅度也有1%左右。
此外,CoSENT还有更快的收敛速度,比如“BERT+CoSENT+ATEC”的原生训练,第一个epoch的valid结果就有48.78,而对应的“Sentence-BERT+ATEC”只有41.54;“RoBERTa+CoSENT+PAWSX”的原生训练,第一个epoch的valid结果就有57.66,而对应的“Sentence-RoBERTa+PAWSX”只有10.84;等等。
联系与区别 #
可能有的读者会问式$\eqref{eq:cosent}$或式$\eqref{eq:cosent-2}$跟SimCSE或对比学习有什么不同?从损失函数的形式上来看两者确有一点相似之处,但含义完全不同的。
标准的SimCSE是只需要正样本对的(通过Dropout或者人工标注构建),然后它将batch内的所有其他样本都视为负样本;而有监督版的SimCSE则是需要三元组的数据,它实际上就是把困难样本补充到标准的SimCSE上,即负样本不只有batch内的所有其他样本,还有标注的困难样本,但同时正样本依然不能缺,所以需要“(原始句子, 相似句子, 不相似句子)”的三元组数据。
至于CoSENT,它只用到了标注好的正负样本对,也不包含随机采样batch内的其他样本来构建负样本的过程,我们也可以将它理解为对比学习,但它是“样本对”的对比学习,而不是像SimCSE的“样本”对比学习,也就是说,它的“单位”是一对句子而不是一个句子。
文章小结 #
本文提出了一种新的有监督句向量方案CoSENT(Cosine Sentence),相比于InferSent和Sentence-BERT,它的训练过程更贴近预测,并且实验显示,CoSENT在收敛速度和最终效果上都普遍比InferSent和Sentence-BERT要好。
转载到请包括本文地址:https://spaces.ac.cn/archives/8847
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jan. 06, 2022). 《CoSENT(一):比Sentence-BERT更有效的句向量方案 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/8847
@online{kexuefm-8847,
title={CoSENT(一):比Sentence-BERT更有效的句向量方案},
author={苏剑林},
year={2022},
month={Jan},
url={\url{https://spaces.ac.cn/archives/8847}},
}










January 7th, 2022
公式6里面$e^{λ(cos(uk,ul)−cos(ui,uj))}$,如果负样本和正样本都预测正确,即使负样本cos结果为-1,正样结果本为1,结果为$e^{-2λ}$,loss也不为0,是不是类似于公式$3$,设置一个阈值$log(1+max(0,e^{λ(cos(uk,ul)−cos(ui,uj))}-thredhold)$更合理一些。
按照$\lambda=20$来算,$e^{-40}\approx 10^{-17}$,足够接近于0了~
January 8th, 2022
苏神,有问题想要请教下
"所以我们加上绝对值变成|u−v|,将球面变为锥形",我理解取绝对值是对某一维以原点为中心做了折叠,那应该是把球面变为半球面了,为什么是锥形呢?
你想一下,一个圆心在原点的单位圆,如果只保留$x,y$都大于等于零的部分,它是一个半圆还是一个扇形?
有道理!感谢苏神点拨。
其实是对每一维都做了折叠,就是一个很细的锥形了。
January 9th, 2022
苏神,关于|u-v|取绝对值的解释,主要还是线性不可分,是不是直接拼接u^2 v^2也可以
另外这个感觉和margin loss有点像?loss = max(0, margin + neg - pos),本质都是希望拉远正样本和负样本的距离?
1、我认为前提是$|u-v|$本身有聚类倾向,$[u^2, v^2]$我没感觉它有聚类倾向;
2、可以参考“联系与区别”一节,CoSENT的单位的“样本对”,是要拉开正样本对和负样本对的距离,这才是它跟旧方案的本质区别。
January 9th, 2022
[...]KeyBERT中其实支持选择编码模型的,中文选择了多语言paraphrase-multilingual-MiniLM-L12-v2481M的大模型。既然SBERT编码句向量这个思路得到了验证,在解决中文问题时,可选择的句向量模型就很多了。比如苏神开放的SimBERT,以及进一步微调过的模型RoFormer-Sim,都可以做句向量。最近刚出的CoSENT比Sentence-BERT更有效的句向量方案[...]
January 11th, 2022
您好,想请教一个问题。Sentence Bert之所以采取这种训练和inference有差异的方式,而不是在inference阶段同样将两个句子输入模型后取模型输出的分数作为相似度得分,是主要出于速度上的考虑么?还是也有效果上的影响在这里面?
主要是速度吧。因为余弦相似度也就是内积的一种,用内积做检索可以用Faiss等工具加速。
January 11th, 2022
sbert之所以有效,会不会是因为(u, v)和(v, u)同时都会参与训练?
逻辑关系在哪?
January 12th, 2022
请教两个问题哈,第一个是请问这个方式没有试过不同数据分布对结果的影响,根据loss公式,在极端情况下假如这个batch全为正例或者负例那么loss为零不会更新模型,所以是不是尽量保证每个batch的正负比例一致训练效果会更好。另一个是batch_size对模型的效果的影响如何,在CSE方式中batch_size越大能够看到更多的负例数据有助于效果的提升,你这个方式理论上batch_size越大也会看到更多的正负例比较数据,我不清楚是不是也会效果更好,以及影响有没有CSE方式那么大。
你说的两点,都没有专门实验过~不过可以大致说一下。
如果batch内全正或者全负,确实是不会更新的,所以尽量保证batch内正负样本都有,但是不是均衡最优,其实我也不确定,但感觉不见得均衡后会更好~
至于batch_size,加大batch_size可能会有正面作用,但CoSENT没有在batch内采样负样本的做法,所以估计这个作用不会特别大,可能也就是加速收敛的作用。
事实上,除了你考虑的点外,另外一个有影响的点是引入margin,确保正负样本对不止要分开,还要分开得更明显一些。这个简单实验了一下,确实可以拉开差距,但对效果没有明显影响。
多谢苏神解惑
January 14th, 2022
请教两个问题,第一,simcse有监督的训练方式将该batch内其他样本都作为负样本,是否会存在假的负样本,比如:q1,q1_pos,q1_neg; q1,q1_pos2,q1_neg2;实际训练的时候可能会将q1_pos2也作为负样本,这种情况是否会影响simcse的效果?第二,我们有对比CoSENT和simcse在有监督样本情况下的效果呢。谢谢。
1、从负样本的角度来看,是可能存在假负样本,但比例很少,从学习互信息的角度来看,这倒不成问题;
2、在有监督情况下,CoSENT和SimCSE是不对等的,无法直接比较,因为CoSENT只需要正样本对和负样本对这样的二元组数据,而SimCSE需要三元组数据(本文已经说过)。
感谢您的回答,不太明白您说的“从学习互信息的角度来看,这倒不成问题”,这个怎么理解呢,感谢。
你可以看一下FlatNCE的原文。将对比学习理解为互信息估计,分母那一项是某个样本与全体样本一一组合的平均,既然是全体样本,那么自然会包含真正的负样本以及“假”的负样本了。
January 27th, 2022
"如果我们用式(1)作为损失函数,那么正样本对的目标是1、负样本对的目标是-1,如果我们用式(2)作为损失函数,那么正样本对的目标是1、负样本对的目标是0。"这是咋算出来的
以$\eqref{eq:cos-1}$为例,对于正样本对$t=1$,此时它等于$1-\cos(u,v)$,当loss为0时,$\cos(u,v)=1$,也就是正样本对的目标cos是1;对于负样本对$t=0$,此时它等于$1+\cos(u,v)$,当loss为0时,$\cos(u,v)=-1$,也就是负样本对的目标cos是-1。
February 9th, 2022
在本文对应的代码中,为什么要乘以e的12次方呢?
y_pred = K.reshape(y_pred - (1 - y_true) * 1e12, [-1])
因为需要排除掉不需要计算的部分。
mask原理参考:https://kexue.fm/archives/6810#Mask