《自然极值》系列——6.最速降线的解答
By 苏剑林 | 2010-12-10 | 79831位读者 |通过上一小节的小故事,我们已经能够基本了解最速降线的内容了,它就是要我们求出满足某一极值条件的一个未知函数,由于函数是未知的,因此这类问题被称为“泛分析”。其中还谈到,伯努利利用费马原理巧妙地得出了答案,那么我们现在就再次回顾历史,追寻伯努利的答案,并且寻找进一步的应用。
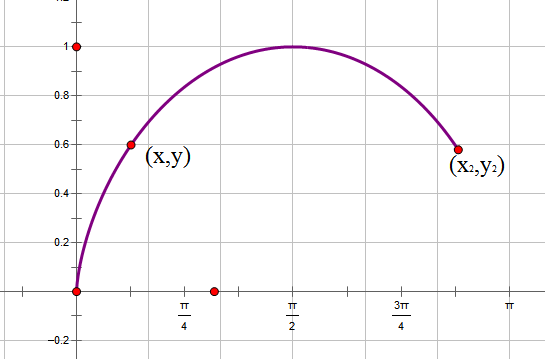
为了计算方便,我们把最速降线倒过来,把初始点设置在原点。在下落过程中,重力势能转化为动能,因此,在点(x,y)处有$\frac{1}{2} mv^2=mgy\Rightarrow v=\sqrt{2gy}$,由于纯粹为了探讨曲线形状,所以我们使g=0.5,即$v=\sqrt{y}$。在点(x,y)处所走的路程为$ds=\sqrt{dy^2+dx^2}=\sqrt{\dot{y}^2+1}dx$,所以时间为$dt=\frac{ds}{v}=\frac{\sqrt{\dot{y}^2+1}dx}{\sqrt{y}}$,于是最速降线问题就是求使$t=\int_0^{x_2} \frac{\sqrt{\dot{y}^2+1}dx}{\sqrt{y}}$最小的函数。
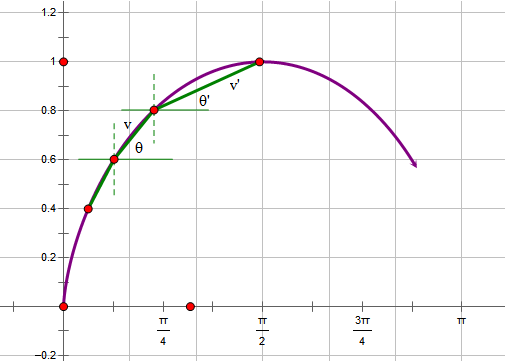
按照伯努利的思路,我们将最速降线视为一条光路,把其水平等距分割成无限小份,那么每一份都应该满足光的折射定律,如图所示,我们将有
$$\frac{v}{\cos\theta}=\frac{v'}{\cos\theta'}=...=Const$$
Const表示常数。由于
$$\cos\theta=\frac{1}{\sqrt{1+\tan^2 \theta}}=\frac{1}{\sqrt{1+\dot{y}^2}}$$
所以得出
$$v^2(1+\dot{y}^2)=Const\tag{1}$$
请注意,我们还没有用到$v=\sqrt{y}$这一条件,也就是说(1)式并非局限于本题目。那么,哪种类型的题目可以应用(1)式呢?答案是“当速度v的表达式中仅仅显含y”的题目,换句话说,当v的表达式中仅仅显含y时,满足
$$t=\int_{x_1}^{x_2} \frac{\sqrt{\dot{y}^2+1}dx}{v}$$
取最小值的函数由(1)式算出。
为什么会这样呢?这需要回想我们的光学知识了。应用光学的折射定律首先得作出“法线”,而“法线”是怎么作出的呢?哦,它垂直于两种不同介质间的接触面的切面。光在两种不同介质间的不同表现就是传播速度的不同,因此,用数学的语言讲,“两种不同介质间的接触面”就是等速面。
若$v=v(x,y)$,显然,每一个速度的等速面(放到二维,退化成等速线)方程都可以表示成$v_c=v(x,y)$,$v_c$是代表速度的常数。既然如此,将其两边微分,就可以得到(这...已经有点深入了,下式涉及到偏导数,还没有了解的朋友可以跳过)
$$0=\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\dot{y}=0\tag{2}$$
这样就可以求出在点(x,y)出的速度切面(线)的斜率。对于v仅仅显含y的情况,$\dot{y}$是恒等于0的,因此每条法线都垂直于x轴。于是我们才能够按照伯努利的思路,“把其水平等距分割成无限小份”,要不然,这一步已经不成立了。对于v不单纯显含y的情况,还是可以利用(2)式求出斜率,再进行转角的,麻烦但奏效;不过如果v还含有诸如$\dot{y}$的导数项,那么此思路就失效了。
回到最速降线问题,将$v=\sqrt{y}$代入(1),就可以得到
$$y(1+\dot{y}^2)=C_1$$
$\dot{y}=\sqrt{\frac{C_1}{y}-1}$,即$x=\int \sqrt{\frac{y}{C_1-y}}dy$
令$y=C_1(\frac{1}{2}-\frac{1}{2} cos 2t)=C_1 sin^2 t$,代入得$x=\int 2C_1 sin^2 t dt=C_1(t-\frac{1}{2} sin 2t +C_2)$;根据初始条件,该曲线过(0,0),得到$C_2=0$;另一个常数可以根据另外一点得出。于是最速降线为
$$\begin{aligned}x=C_1(t-\frac{1}{2} \sin 2t) \\ y=C_1(\frac{1}{2}-\frac{1}{2} \cos 2t)\end{aligned}$$
可见,这是一条摆线,或曰旋轮线、等时曲线。
【摆线的定义】
摆线是数学中众多的迷人曲线之一.它是这样定义的:一个圆沿一直线缓慢地滚动,则圆上一固定点所经过的轨迹称为摆线.
参数方程为
$$x=r(t- \sin t),y=r(1- \cos t)$$
到17世纪,人们发现摆线具有如下性质:
1.它的长度等于旋转圆直径的4倍.尤为令人感兴趣的是,它的长度是一个不依赖于π的有理数.
2.在弧线下的面积,是旋转圆面积的三倍.
3.圆上描出摆线的那个点,具有不同的速度——事实上,在特定的地方它甚至是静止的.
4.当弹子从一个摆线形状的容器的不同点放开时,它们会同时到达底部。
转载到请包括本文地址:https://spaces.ac.cn/archives/1107
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Dec. 10, 2010). 《《自然极值》系列——6.最速降线的解答 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/1107
@online{kexuefm-1107,
title={《自然极值》系列——6.最速降线的解答},
author={苏剑林},
year={2010},
month={Dec},
url={\url{https://spaces.ac.cn/archives/1107}},
}











December 12th, 2010
你不是说要用自己的方法解决吗
用自己的方法解决悬链线问题
December 12th, 2010
奇妙的数学
January 3rd, 2011
对于v仅仅显含y的情况,$\dot{y}$是恒等于0的
这句是为什么,没看懂
也许是速度仅与纵坐标有关吧。
这是的$\dot{y}$仅仅是指“等速线(面)”切线的斜率。当v不显含x时,显然是平行于x轴的
February 23rd, 2011
小苏,你博文里的坐标图是用什么画的?是截图吗?
几何画板。