27
Sep
必须要GPT3吗？不，BERT的MLM模型也能小样本学习
By 苏剑林 | 2020-09-27 | 152800位读者 | 引用大家都知道现在GPT3风头正盛，然而，到处都是GPT3、GPT3地推，读者是否记得GPT3论文的名字呢？事实上，GPT3的论文叫做《Language Models are Few-Shot Learners》，标题里边已经没有G、P、T几个单词了，只不过它跟开始的GPT是一脉相承的，因此还是以GPT称呼它。顾名思义，GPT3主打的是Few-Shot Learning，也就是小样本学习。此外，GPT3的另一个特点就是大，最大的版本多达1750亿参数，是BERT Base的一千多倍。
BERT的MLM模型简单示意图
正因如此，前些天Arxiv上的一篇论文《It's Not Just Size That Matters: Small Language Models Are Also Few-Shot Learners》便引起了笔者的注意，意译过来就是“谁说一定要大的？小模型也可以做小样本学习”。显然，这标题对标的就是GPT3，于是笔者饶有兴趣地点进去看看是谁这么有勇气挑战GPT3，又是怎样的小模型能挑战GPT3？经过阅读，原来作者提出通过适当的构造，用BERT的MLM模型也可以做小样本学习，看完之后颇有一种“原来还可以这样做”的恍然大悟感～在此与大家分享一下。
10
Sep
变分自编码器（六）：从几何视角来理解VAE的尝试
By 苏剑林 | 2020-09-10 | 69643位读者 | 引用前段时间公司组织技术分享，轮到笔者时，大家希望我讲讲VAE。鉴于之前笔者也写过变分自编码器系列，所以对笔者来说应该也不是特别难的事情，因此就答应了下来，后来仔细一想才觉得犯难：怎么讲才好呢？
变分自编码器示意图
对于VAE来说，之前笔者有两篇比较系统的介绍：《变分自编码器（一）：原来是这么一回事》和《变分自编码器（二）：从贝叶斯观点出发》。后者是纯概率推导，对于不做理论研究的人来说其实没什么意义，也不一定能看得懂；前者虽然显浅一点，但也不妥，因为它是从生成模型的角度来讲的，并没有说清楚“为什么需要VAE”（说白了，VAE可以带来生成模型，但是VAE并不一定就为了生成模型），整体风格也不是特别友好。
笔者想了想，对于大多数不了解但是想用VAE的读者来说，他们应该只希望大概了解VAE的形式，然后想要知道“VAE有什么作用”、“VAE相比AE有什么区别”、“什么场景下需要VAE”等问题的答案，对于这种需求，上面两篇文章都无法很好地满足。于是笔者尝试构思了VAE的一种几何图景，试图从几何角度来描绘VAE的关键特性，在此也跟大家分享一下。
10
Jun
无监督分词和句法分析！原来BERT还可以这样用
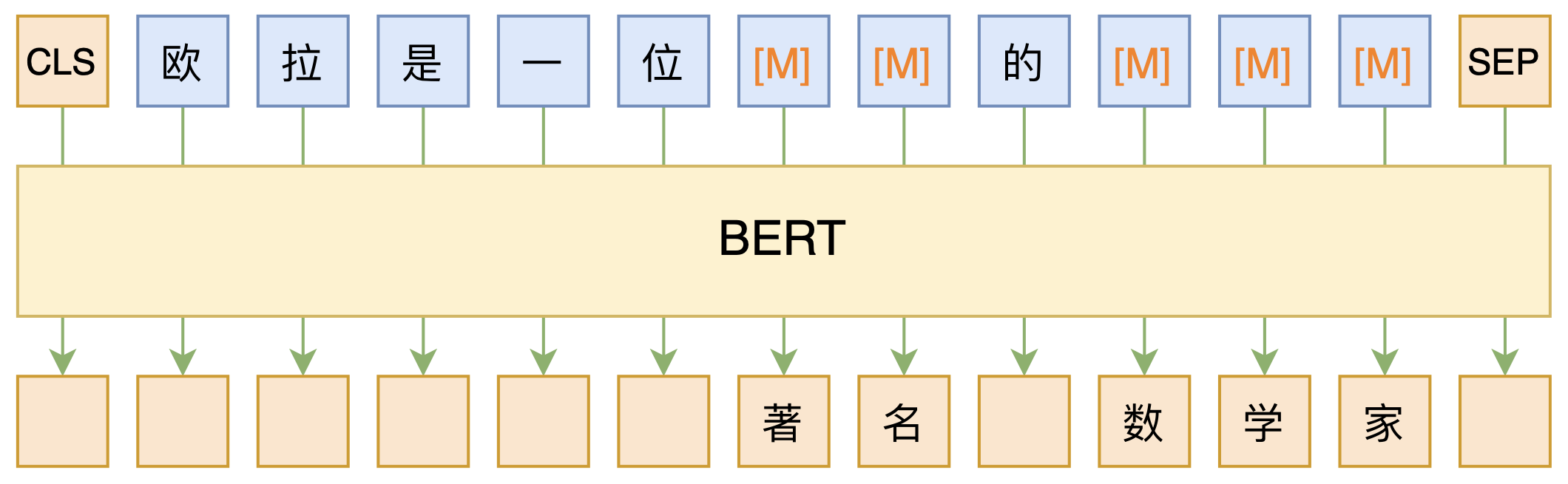
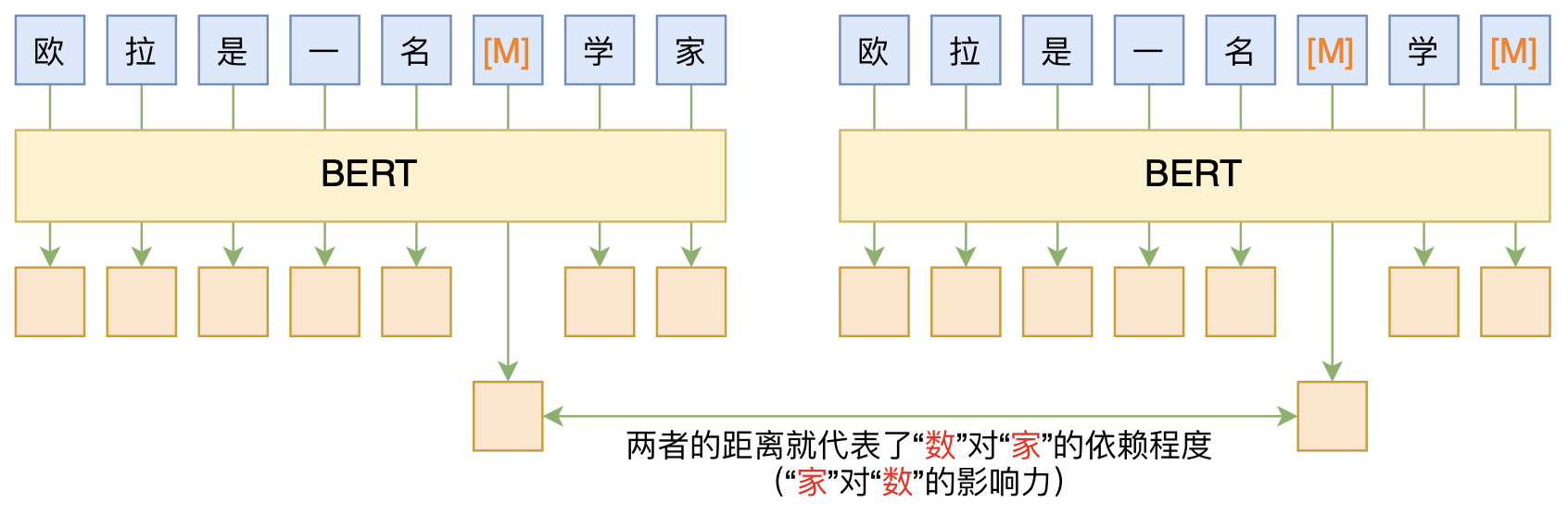
By 苏剑林 | 2020-06-10 | 85463位读者 | 引用BERT的一般用法就是加载其预训练权重，再接一小部分新层，然后在下游任务上进行finetune，换句话说一般的用法都是有监督训练的。基于这个流程，我们可以做中文的分词、NER甚至句法分析，这些想必大家就算没做过也会有所听闻。但如果说直接从预训练的BERT（不finetune）就可以对句子进行分词，甚至析出其句法结构出来，那应该会让人感觉到意外和有趣了。
本文介绍ACL 2020的论文《Perturbed Masking: Parameter-free Probing for Analyzing and Interpreting BERT》，里边提供了直接利用Masked Language Model（MLM）来分析和解释BERT的思路，而利用这种思路，我们可以无监督地做到分词甚至句法分析。
基于BERT的“token-token”相关度计算图示
6
May
变分自编码器（五）：VAE + BN = 更好的VAE
By 苏剑林 | 2020-05-06 | 203676位读者 | 引用本文我们继续之前的变分自编码器系列，分析一下如何防止NLP中的VAE模型出现“KL散度消失（KL Vanishing）”现象。本文受到参考文献是ACL 2020的论文《A Batch Normalized Inference Network Keeps the KL Vanishing Away》的启发，并自行做了进一步的完善。
值得一提的是，本文最后得到的方案还是颇为简洁的——只需往编码输出加入BN（Batch Normalization），然后加个简单的scale——但确实很有效，因此值得正在研究相关问题的读者一试。同时，相关结论也适用于一般的VAE模型（包括CV的），如果按照笔者的看法，它甚至可以作为VAE模型的“标配”。
最后，要提醒读者这算是一篇VAE的进阶论文，所以请读者对VAE有一定了解后再来阅读本文。
VAE简单回顾
这里我们简单回顾一下VAE模型，并且讨论一下VAE在NLP中所遇到的困难。关于VAE的更详细介绍，请读者参考笔者的旧作《变分自编码器（一）：原来是这么一回事》、《变分自编码器（二）：从贝叶斯观点出发》等。
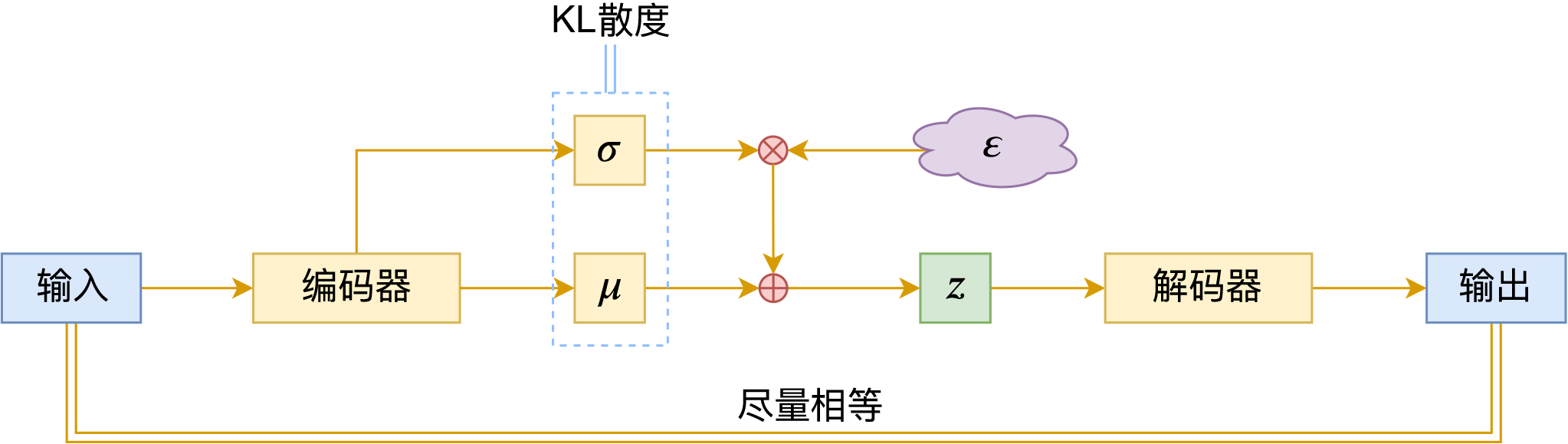
VAE的训练流程
VAE的训练流程大概可以图示为
VAE训练流程图示
20
Apr
EAE：自编码器 + BN + 最大熵 = 生成模型
By 苏剑林 | 2020-04-20 | 58706位读者 | 引用生成模型一直是笔者比较关注的主题，不管是NLP和CV的生成模型都是如此。这篇文章里，我们介绍一个新颖的生成模型，来自论文《Batch norm with entropic regularization turns deterministic autoencoders into generative models》，论文中称之为EAE（Entropic AutoEncoder）。它要做的事情给变分自编码器（VAE）基本一致，最终效果其实也差不多（略优），说它新颖并不是它生成效果有多好，而是思路上的新奇，颇有别致感。此外，借着这个机会，我们还将学习一种统计量的估计方法——$k$邻近方法，这是一种很有用的非参数估计方法。
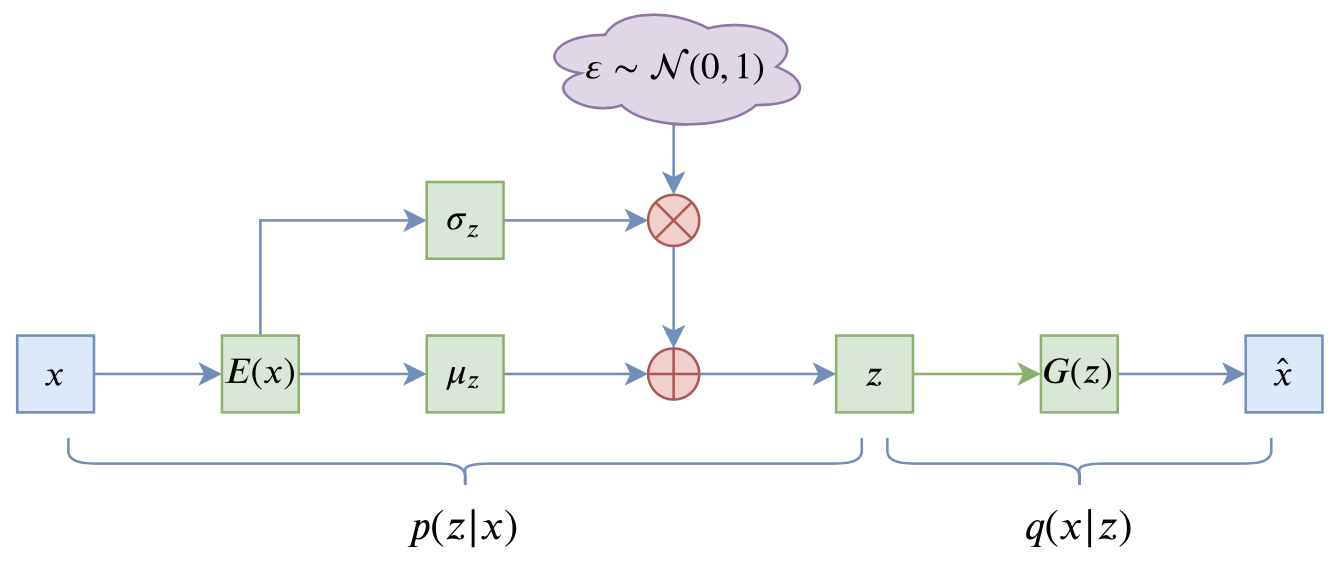
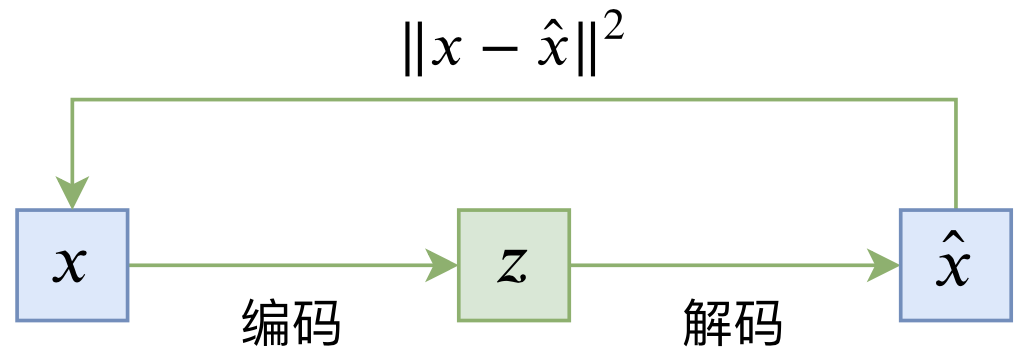
自编码器vs生成模型
普通的自编码器是一个“编码-解码”的重构过程，如下图所示：
典型自编码器示意图
其loss一般为
\begin{equation}L_{AE} = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - \hat{x}\right\Vert^2\right] = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - D(E(x))\right\Vert^2\right]\end{equation}
19
Oct
最小熵原理（五）：“层层递进”之社区发现与聚类
By 苏剑林 | 2019-10-19 | 153547位读者 | 引用让我们不厌其烦地回顾一下：最小熵原理是一个无监督学习的原理，“熵”就是学习成本，而降低学习成本是我们的不懈追求，所以通过“最小化学习成本”就能够无监督地学习出很多符合我们认知的结果，这就是最小熵原理的基本理念。
这篇文章里，我们会介绍一种相当漂亮的聚类算法，它同样也体现了最小熵原理，或者说它可以通过最小熵原理导出来，名为InfoMap，或者MapEquation。事实上InfoMap已经是2007年的成果了，最早的论文是《Maps of random walks on complex networks reveal community structure》，虽然看起来很旧，但我认为它仍是当前最漂亮的聚类算法，因为它不仅告诉了我们“怎么聚类”，更重要的是给了我们一个“为什么要聚类”的优雅的信息论解释，并从这个解释中直接导出了整个聚类过程。
一个复杂有向图网络示意图。图片来自InfoMap最早的论文《Maps of random walks on complex networks reveal community structure》
当然，它的定位并不仅仅局限在聚类上，更准确地说，它是一种图网络上的“社区发现”算法。所谓社区发现（Community Detection），大概意思是给定一个有向/无向图网络，然后找出这个网络上的“抱团”情况，至于详细含义，大家可以自行搜索一下。简单来说，它跟聚类相似，但是比聚类的含义更丰富。（还可以参考《什么是社区发现?》）
9
Sep
重新写了之前的新词发现算法：更快更好的新词发现
By 苏剑林 | 2019-09-09 | 96970位读者 | 引用新词发现是NLP的基础任务之一，主要是希望通过无监督发掘一些语言特征（主要是统计特征），来判断一批语料中哪些字符片段可能是一个新词。本站也多次围绕“新词发现”这个话题写过文章，比如：
在这些文章之中，笔者觉得理论最漂亮的是《基于语言模型的无监督分词》，而作为新词发现算法来说综合性能比较好的应该是《更好的新词发现算法》，本文就是复现这篇文章的新词发现算法。
24
Jun
VQ-VAE的简明介绍：量子化自编码器
By 苏剑林 | 2019-06-24 | 323288位读者 | 引用印象中很早之前就看到过VQ-VAE，当时对它并没有什么兴趣，而最近有两件事情重新引起了我对它的兴趣。一是VQ-VAE-2实现了能够匹配BigGAN的生成效果（来自机器之心的报道）；二是我最近看一篇NLP论文《Unsupervised Paraphrasing without Translation》时发现里边也用到了VQ-VAE。这两件事情表明VQ-VAE应该是一个颇为通用和有意思的模型，所以我决定好好读读它。
个人复现的VQ-VAE在CelebA上的重构效果。可以留意到细节保留得还不错，但稍微放大后能留意到仍有一些模糊感。
最近评论