意犹未尽——继续光学曲线

在《为什么是抛物线？——聚光面研究》这篇文章里头，我们从光学性质出发，推导出了符合该光学性质的曲线为抛物线，同时我们也不禁感到了向量分析的美妙。也许有的读者会意犹未尽：圆锥曲线有三种，文章只介绍了一种。那好，在这篇文章里，我们就从另外两个光学性质出发，推导出符合这两个光学性质的曲线（椭圆、双曲线）。

（注：在下面的描述中，橙色加粗向量表示光线，曲线表示反射面。）

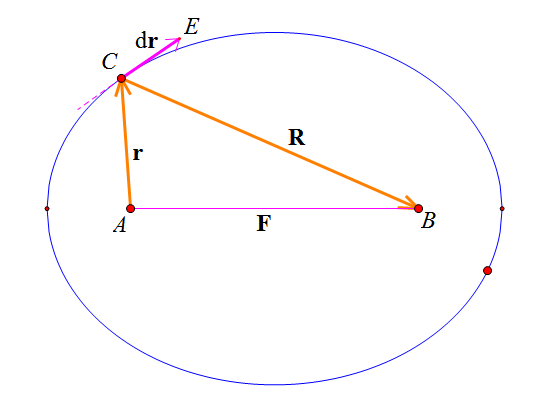
一、从一个点发出的光线经过曲线（面）反射后汇集到另外一个点上。

这是椭圆的一个性质，我们要证明只有椭圆才符合它。如上图用AC向量$\vec{r}$来表示该曲线的轨迹，用$\vec{F}$表示AB间的距离向量（这是一个常向量），且$\vec{R}=\vec{F}-\vec{r}$，同时记$|\vec{r}|=r,|\vec{R}|=R$（如无说明，科学空间都采用这两个记法）。
根据光的反射定律，向量$\vec{R}$和$\vec{r}$与CE($d\vec{r}$)的夹角是相等的，所以有

$$\frac{\vec{r}\cdot d\vec{r}}{r}=\frac{\vec{R}\cdot d\vec{r}}{R}$$

别忘了联系$\vec{R}=\vec{F}-\vec{r}$，我们有$d\vec{r}=-d(\vec{F}-\vec{r})=-d\vec{R}$，代入上式即得

$$\frac{\vec{r}\cdot d\vec{r}}{r}+\frac{\vec{R}\cdot d\vec{R}}{R}=0$$

又回到了恒等式$\vec{r}\cdot d\vec{r}=rdr$来了，上式等价于$dr+dR=0$，两端积分即有

$$r+R=C\Rightarrow |\vec{r}|+|\vec{F}-\vec{r}|=C$$

这不就是椭圆的定义吗？于是问题被我们解决了。紧接着，我们来执行下一个任务...

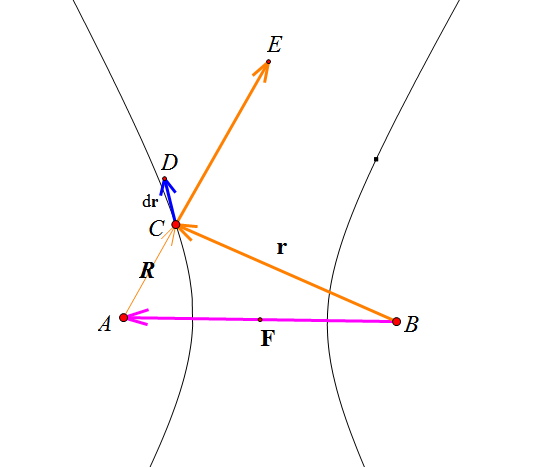
二、从一个点发出的光线经过曲线（面）反射后，宛如从另外一个点上发出一样。

有了对椭圆和抛物线两者光学性质的分析经验，相信读者已经累积了一些方法，因此不再重复叙述推导过程，直接写出

$$\begin{aligned}\vec{R}=\vec{r}-\vec{F} \\ \frac{\vec{r}\cdot d\vec{r}}{r}=\frac{\vec{R}\cdot d\vec{r}}{R}\end{aligned}$$

$d\vec{r}=d(\vec{r}-\vec{F})=d\vec{R}$，代入上式即得

$\frac{\vec{r}*d\vec{r}}{r}-\frac{\vec{R}*d\vec{R}}{R}=0$，等价于

$dr-dR=0$，两端积分即有

$$r-R=C\Rightarrow |\vec{r}|-|\vec{R}|=C$$

同样，这是双曲线的定义！于是问题探讨结束。我们再次通过向量简明地解决了困扰我们的问题！

最后附上一些关于圆锥曲线的历史（网络搜集）：

历史上第一个考查圆锥曲线的是梅纳库莫斯（公元前375年—325年）；大约100年后，阿波罗尼奥更详尽、系统地研究了圆锥曲线。他们两位对圆锥曲线的研究是很实在的：考察不同倾斜角的平面截圆锥其切口所得到的曲线，也就是说如果切口与底面所夹的角小于母线与底面所夹的角，则切口呈现椭圆；若两角相等，则切口呈现抛物线；若前者大于后者，则切口呈现双曲线。并且，阿波罗尼奥还进一步研究了这些圆锥曲线的光学性质，比如椭圆，他发现如果把椭圆焦点F一侧做成镜面，并在F处放置光源，那么经过椭圆镜反射的光线全部通过另一个焦点F。热也和光一样发生反射，所以这时便会被烤焦，这也就是焦点名称的由来。据说这一发现是他在研究椭圆的作法（也就是现行教材中一开始介绍的作法）时得出的。

而圆锥曲线真正从后台走上前台，从学术的象牙塔中进入现实生活的世界里，应归功于德国天文学家开普勒（公元1571年—1630年），开普勒在长期的天文观察及对记录的数据分析中，发现了著名的“开普勒三定律”，其中第一条是：“行星在包含太阳的平面内运动，划出以太阳为焦点的椭圆”，就这样，梅纳库莫斯和阿波罗尼奥出于数学爱好而研究的曲线在近2000年之后于天文学的舞台上登场了。后来哈雷又利用圆锥曲线理论及计算方法准确地预测到哈雷彗星与地球最近点的时刻，1758年在哈雷逝世16年之后，哈雷彗星与地球如期而遇，这引起了全欧洲、乃至全世界的轰动，也进一步推动人们对圆锥曲线研究兴趣的提升。

转载到请包括本文地址：https://spaces.ac.cn/archives/1058

更详细的转载事宜请参考：《科学空间FAQ》