科学空间|Scientific Spaces

在这篇文章中，我们将探讨一个被称为“梯度流（Gradient Flow）”的概念。简单来说，梯度流是将我们在用梯度下降法中寻找最小值的过程中的各个点连接起来，形成一条随（虚拟的）时间变化的轨迹，这条轨迹便被称作“梯度流”。在文章的后半部分，我们将重点讨论如何将梯度流的概念扩展到概率空间，从而形成“Wasserstein梯度流”，为我们理解连续性方程、Fokker-Planck方程等内容提供一个新的视角。

梯度下降

假设我们想搜索光滑函数$f(\boldsymbol{x})$的最小值，常见的方案是梯度下降（Gradient Descent），即按照如下格式进行迭代：
\begin{equation}\boldsymbol{x}_{t+1} = \boldsymbol{x}_t -\alpha \nabla_{\boldsymbol{x}_t}f(\boldsymbol{x}_t)\label{eq:gd-d}\end{equation}
如果$f(\boldsymbol{x})$关于$\boldsymbol{x}$是凸的，那么梯度下降通常能够找到最小值点；相反，则通常只能收敛到一个“驻点”——即梯度为0的点，比较理想的情况下能收敛到一个极小值（局部最小值）点。这里没有对极小值和最小值做严格区分，因为在深度学习中，即便是收敛到一个极小值点也是很难得的了。

点击阅读全文...

众所周知，在深度学习之前，机器学习是SVM（Support Vector Machine，支持向量机）的天下，曾经的它可谓红遍机器学习的大江南北，迷倒万千研究人员，直至今日，“手撕SVM”仍然是大厂流行的面试题之一。然而，时过境迁，当深度学习流行起来之后，第一个革的就是SVM的命，现在只有在某些特别追求效率的场景以及大厂的面试题里边，才能看到SVM的踪迹了。

峰回路转的是，最近Arxiv上的一篇论文《Every Model Learned by Gradient Descent Is Approximately a Kernel Machine》做了一个非常“霸气”的宣言：

任何由梯度下降算法学出来的模型，都是可以近似看成是一个SVM！

这结论真不可谓不“霸气”，因为它已经不只是针对深度学习了，而是只要你用梯度下降优化的，都不过是一个SVM（的近似）。笔者看了一下原论文的分析，感觉确实挺有意思也挺合理的，有助于加深我们对很多模型的理解，遂跟大家分享一下。

点击阅读全文...

自SimCLR以来，CV中关于无监督特征学习的工作层出不穷，让人眼花缭乱。这些工作大多数都是基于对比学习的，即通过适当的方式构造正负样本进行分类学习的。然而，在众多类似的工作中总有一些特立独行的研究，比如Google的BYOL和最近的SimSiam，它们提出了单靠正样本就可以完成特征学习的方案，让人觉得耳目一新。但是没有负样本的支撑，模型怎么不会退化（坍缩）为一个没有意义的常数模型呢？这便是这两篇论文最值得让人思考和回味的问题了。

其中SimSiam给出了让很多人都点赞的答案，但笔者觉得SimSiam也只是把问题换了种说法，并没有真的解决这个问题。笔者认为，像SimSiam、GAN等模型的成功，很重要的原因是使用了基于梯度的优化器（而非其他更强或者更弱的优化器），所以不结合优化动力学的答案都是不完整的。在这里，笔者尝试结合动力学来分析SimSiam不会退化的原因。

SimSiam

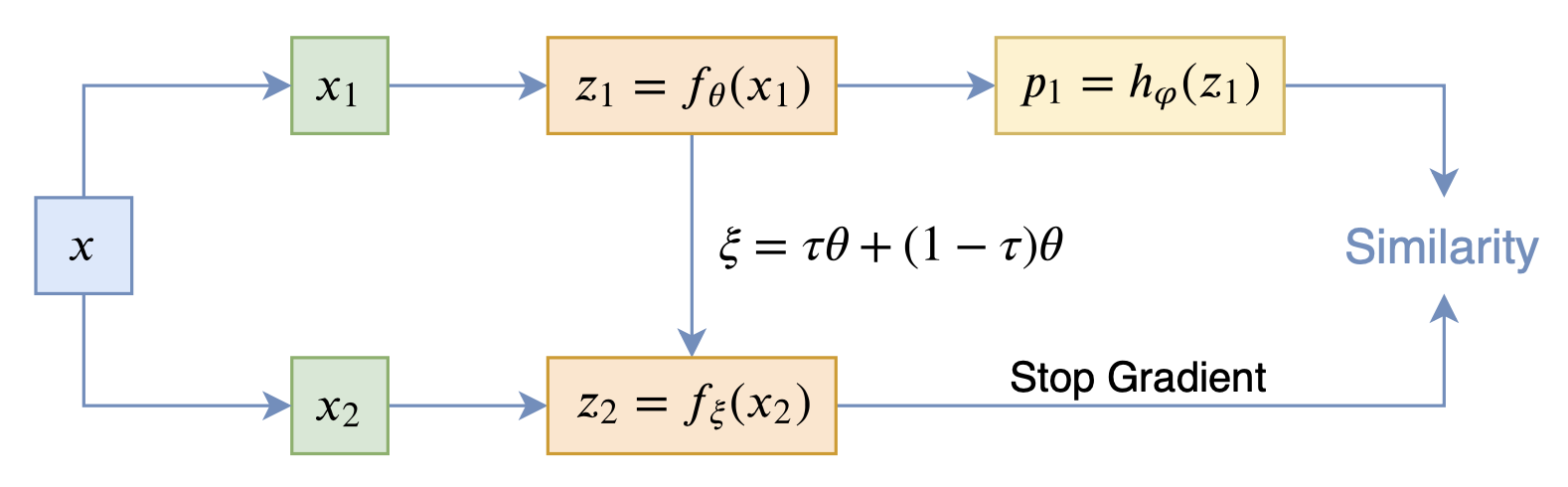
在看SimSiam之前，我们可以先看看BYOL，来自论文《Bootstrap your own latent: A new approach to self-supervised Learning》，其学习过程很简单，就是维护两个编码器Student和Teacher，其中Teacher是Student的滑动平均，Student则又反过来向Teacher学习，有种“左脚踩右脚”就可以飞起来的感觉。示意图如下：

BYOL示意图

点击阅读全文...

本文的主题是“为什么我们需要有限的学习率”，所谓“有限”，指的是不大也不小，适中即可，太大容易导致算法发散，这不难理解，但为什么太小也不好呢？一个容易理解的答案是，学习率过小需要迭代的步数过多，这是一种没有必要的浪费，因此从“节能”和“加速”的角度来看，我们不用过小的学习率。但如果不考虑算力和时间，那么过小的学习率是否可取呢？Google最近发布在Arxiv上的论文《Implicit Gradient Regularization》试图回答了这个问题，它指出有限的学习率隐式地给优化过程带来了梯度惩罚项，而这个梯度惩罚项对于提高泛化性能是有帮助的，因此哪怕不考虑算力和时间等因素，也不应该用过小的学习率。

对于梯度惩罚，本博客已有过多次讨论，在文章《对抗训练浅谈：意义、方法和思考（附Keras实现）》和《泛化性乱弹：从随机噪声、梯度惩罚到虚拟对抗训练》中，我们就分析了对抗训练一定程度上等价于对输入的梯度惩罚，而文章《我们真的需要把训练集的损失降低到零吗？》介绍的Flooding技巧则相当于对参数的梯度惩罚。总的来说，不管是对输入还是对参数的梯度惩罚，都对提高泛化能力有一定帮助。

点击阅读全文...

在对GAN的学习和思考过程中，我发现我不仅学习到了一种有效的生成模型，而且它全面地促进了我对各种模型各方面的理解，比如模型的优化和理解视角、正则项的意义、损失函数与概率分布的联系、概率推断等等。GAN不单单是一个“造假的玩具”，而是具有深刻意义的概率模型和推断方法。

作为事后的总结，我觉得对GAN的理解可以粗糙地分为三个阶段：

1、样本阶段：在这个阶段中，我们了解了GAN的“鉴别者-造假者”诠释，懂得从这个原理出发来写出基本的GAN公式（如原始GAN、LSGAN），比如判别器和生成器的loss，并且完成简单GAN的训练；同时，我们知道GAN有能力让图片更“真”，利用这个特性可以把GAN嵌入到一些综合模型中。

2、分布阶段：在这个阶段中，我们会从概率分布及其散度的视角来分析GAN，典型的例子是WGAN和f-GAN，同时能基本理解GAN的训练困难问题，比如梯度消失和mode collapse等，甚至能基本地了解变分推断，懂得自己写出一些概率散度，继而构造一些新的GAN形式。

3、动力学阶段：在这个阶段中，我们开始结合优化器来分析GAN的收敛过程，试图了解GAN是否能真的达到理论的均衡点，进而理解GAN的loss和正则项等因素如何影响的收敛过程，由此可以针对性地提出一些训练策略，引导GAN模型到达理论均衡点，从而提高GAN的效果。

点击阅读全文...

最近把优化算法跟动力学结合起来思考得越来越起劲了，这是优化算法与动力学系列的第三篇，我有预感还会有第4篇，敬请期待～

简单来个剧情回顾：第一篇中我们指出了其实SGD相当于常微分方程（ODE）的数值解法：欧拉法；第二篇我们还是数值解法的误差分析的角度，分析了为什么可以通过梯度来调节学习率，因此也就解释了RMSprop、Adam等算法中，用梯度调节学习率的原理。

本文将给出一个更统一的观点来看待这两个事情，并且试图回答一个更本质的问题：为什么是梯度下降？

（注：本文的讨论没有涉及到动量加速部分。）

点击阅读全文...

在《从动力学角度看优化算法（一）：从SGD到动量加速》一文中，我们提出SGD优化算法跟常微分方程（ODE）的数值解法其实是对应的，由此还可以很自然地分析SGD算法的收敛性质、动量加速的原理等等内容。

在这篇文章中，我们继续沿着这个思路，去理解优化算法中的自适应学习率算法。

RMSprop

首先，我们看一个非常经典的自适应学习率优化算法：RMSprop。RMSprop虽然不是最早提出的自适应学习率的优化算法，但是它却是相当实用的一种，它是诸如Adam这样的更综合的算法的基石，通过它我们可以观察自适应学习率的优化算法是怎么做的。

算法概览

一般的梯度下降是这样的：
$$\begin{equation}\boldsymbol{\theta}_{n+1}=\boldsymbol{\theta}_{n} - \gamma \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}_{n})\end{equation}$$
很明显，这里的$\gamma$是一个超参数，便是学习率，它可能需要在不同阶段做不同的调整。

而RMSprop则是
$$\begin{equation}\begin{aligned}\boldsymbol{g}_{n+1} =& \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}_{n})\\
\boldsymbol{G}_{n+1}=&\lambda \boldsymbol{G}_{n} + (1 - \lambda) \boldsymbol{g}_{n+1}\otimes \boldsymbol{g}_{n+1}\\
\boldsymbol{\theta}_{n+1}=&\boldsymbol{\theta}_{n} - \frac{\tilde{\gamma}}{\sqrt{\boldsymbol{G}_{n+1} + \epsilon}}\otimes \boldsymbol{g}_{n+1}
\end{aligned}\end{equation}$$

点击阅读全文...

在这个系列中，我们来关心优化算法，而本文的主题则是SGD（stochastic gradient descent，随机梯度下降），包括带Momentum和Nesterov版本的。对于SGD，我们通常会关心的几个问题是：

SGD为什么有效？
SGD的batch size是不是越大越好？
SGD的学习率怎么调？
Momentum是怎么加速的？
Nesterov为什么又比Momentum稍好？
...

这里试图从动力学角度分析SGD，给出上述问题的一些启发性理解。

梯度下降

既然要比较谁好谁差，就需要知道最好是什么样的，也就是说我们的终极目标是什么？

训练目标分析

假设全部训练样本的集合为$\boldsymbol{S}$，损失度量为$L(\boldsymbol{x};\boldsymbol{\theta})$，其中$\boldsymbol{x}$代表单个样本，而$\boldsymbol{\theta}$则是优化参数，那么我们可以构建损失函数
$$L(\boldsymbol{\theta}) = \frac{1}{|\boldsymbol{S}|}\sum_{\boldsymbol{x}\in\boldsymbol{S}} L(\boldsymbol{x};\boldsymbol{\theta})\tag{1}$$
而训练的终极目标，则是找到$L(\boldsymbol{\theta})$的一个全局最优点（这里的最优是“最小”的意思）。

点击阅读全文...