19
Jun
向量结合复数：常曲率曲线(1)
By 苏剑林 | 2011-06-19 | 30448位读者 | 引用在之前的一篇向量系列的文章中，我们通过结合物理与向量来巧妙地推导出了曲线（包括平面和空间的）的曲率半径为
$$R=\frac{v^2}{a_c}=\frac{|\dot{\vec{r}}|^3}{|\dot{\vec{r}}\times \ddot{\vec{r}}|}\tag{1}$$
曲率则是曲率半径的导数：$\rho=\frac{1}{R}$。我们反过来思考一下：曲率恒定的平面曲线是否只有圆？
答案貌似是很显然的，我们需要证明一下。
由于只是考虑平面情况，我们先设$\dot{\vec{r}}=(v cos\theta,v sin\theta)=z=ve^{i\theta}$，代入(1)得到
$\frac{\dot{\theta}}{v}=\rho$————(2)
25
Jun
高中数学联赛题目和答案
By 苏剑林 | 2011-06-25 | 26668位读者 | 引用2011年的高中数学联赛拉开帷幕了...
前些天数学老师找了我们两个重点班的8个人，商量了参加今年数学联赛预赛的事情。大家都同意尝试，同时在我的强烈要求之下，增加了两位同学（一位是我的同桌，另外一位是我心目中的“天才生”）。只是老师也没有组织经验，而我上一年有过参赛经验（本来那是高三的玩意儿，我那时一个高二生瞎搅和进去，居然把高三的几个师兄师姐P下去了，意外呀...^_^），老师就把辅导其他九位同学的任务交给我（艰巨...）。
其实我也没有累积多少数学竞赛的知识，我最感兴趣的数学，几乎都不能在数学竞赛中用到。不过既然报名了，还是得准备准备，因此在网上找了最近几年的高中数学联赛试题和答案来看。顺便放到这里共享，供有需要的朋友下载。
5
Jul
最近的那些事儿...
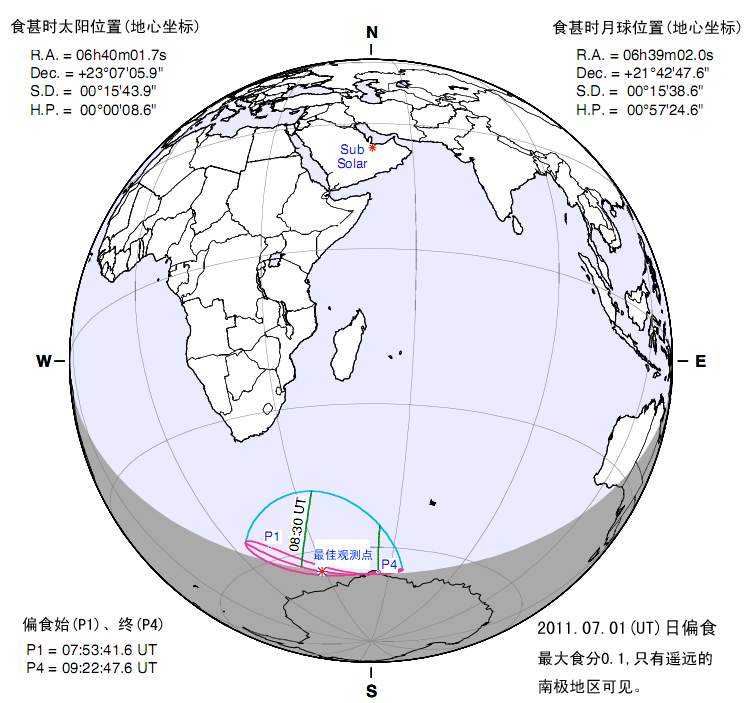
By 苏剑林 | 2011-07-05 | 15719位读者 | 引用
6
Jul
科学空间：2011年7月重要天象
By 苏剑林 | 2011-07-06 | 23424位读者 | 引用
8
Jul
均匀球状星团内恒星的运动
By 苏剑林 | 2011-07-08 | 17847位读者 | 引用我们考虑一个球状的星团，并假设它是各向同性的，即距离球心r处的物质密度ρ只与r有关，ρ=ρ(r)。那么，在半径为r的球形区域内的总质量为：
$$M(r)=\int_0^r 4\pi x^2 \rho(x) dx$$
想象有一颗质量比较小的恒星（其实相对于星团总质量，每一颗恒星的质量都很小）在星团的引力作用下运动（就好像太阳系绕着银河系运动一样），且恒星并没有受到其他物质（如星际尘埃等）的阻力。我们之前已经证明过，各向同性的球壳内部的引力是为0的，那么这种情况下的运动就相当于恒星只受到它到球心处的一个球形区域内的质量的引力吸引。根据万有引力定律，选择星团球心为参考系，可以得出
$$\ddot{\vec{r}}=-GM(r)\frac{\vec{r}}{r^3}$$
10
Jul
明天就出发去夏令营了
By 苏剑林 | 2011-07-10 | 26870位读者 | 引用明天就要飞去北京参加北京大学天文夏令营了。
参加夏令营本来就是喜事，我满怀着喜悦。然而，喜悦之中却有点伤感。伤感的不是夏令营，而是一种别绪，一种难以看到想见的人的无奈。不管怎样，带着想念，好好参与这次的活动，希望能够收获更多的阅历和经验，同时也是一次对许多人梦寐以求的高校——北京大学的旅游和认识，也算是为明年的高考埋下美丽的伏笔
另一方面，暑假的到来意味着高二的结束，其实，当高考结束的那一天起，我们已经是“准高三”学生了。不少人讨论过高三怎么过，也有不少师兄师姐们向我们描述过高三的死板生活，而我的答案只有五个字：高三，好好活！
学着《还珠格格3之天上人间》中的情节，今天我也把自己书架上的书搬上楼去晒晒。
有的书是新买的，有的已经买了一两年了，不管怎样，都拿上去沐浴阳光。
后来才发现，把书搬上去很累很热，把书搬下来重新整理更累更热。整个过程从早上九点开始，直到下午两点才完全结束。
原来，把书搬到太阳下展开的场景很壮观......
当然，晒书只是一个契机，我顺便收拾了一下凌乱的房间，这次算是比较彻底了，一些平常没有清洁的角落都清理了一遍。因为再过几天就正式成为高三了。也许下一次晒书，或者下一次整理，已经是明年的今天了。所以不论怎样，今天都要好好“干一场”！
书籍是人类进步的阶梯，呵呵^_^
25
Jul
最近评论