【竖直上抛】炮弹能够射多高(第二宇宙速度)?
By 苏剑林 | 2010-01-17 | 43644位读者 | 引用一枚炮弹以速度$v_0$向上射出,只考虑重力因素,请问炮弹到达多远的距离后就会开始自由下落?
对于这个问题,我们首先采取的是高中生的做法。考虑地球重力,也就是说炮弹在做加速度为
此即炮弹能够走得最远距离。
但是看了这条式子,我们会发现,这个“距离”始终是有限的。换一句话说,只要$v_0$不趋于无穷大,s就不会无穷大。但是我们还听到过牛顿这样说过:假如炮弹以某个速度(就是我们现在所所说的第二宇宙速度)飞离地球,它就永远不会回来了。两者不是矛盾吗?
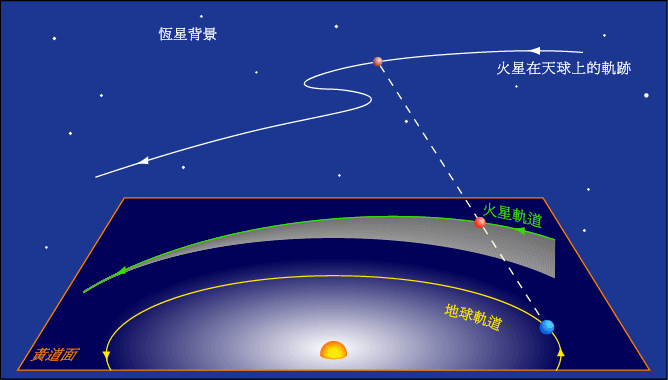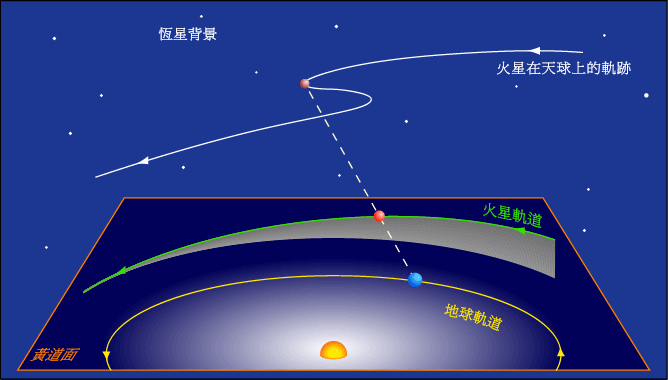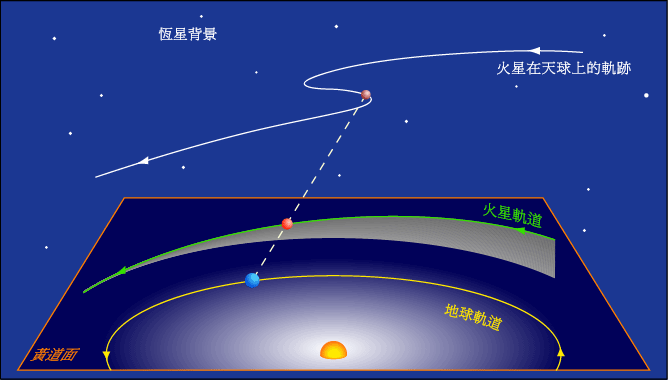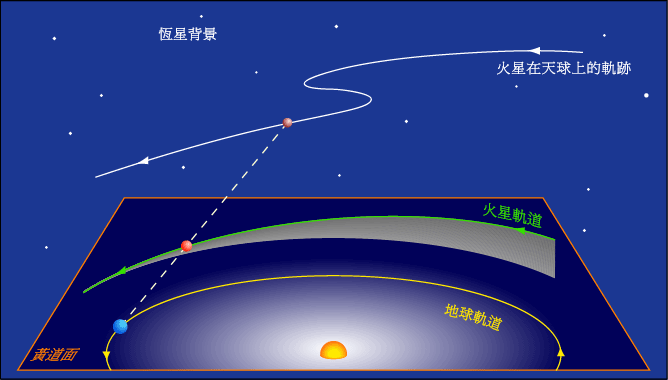
行星的逆行,顺行和留(计算公式)
By 苏剑林 | 2010-04-18 | 65491位读者 | 引用《方程与宇宙》:活力积分和开普勒方程(二)
By 苏剑林 | 2010-03-27 | 59392位读者 | 引用在上一回的讨论中,我们已经解决了大部分的问题,并且表达了找到r或者$\theta$关于时间t的函数的希望。在最后的内容中,我们做了以下工作:
由(7)得到$\dot{\theta}=h/r^2$,代入(6)得到:
$$\ddot{r} -h^2/r^3=-\frac{\mu}{r^2}\tag{10}$$这是一个二阶微分方程,它的解很容易找出,但是这个积分太复杂:
$$\dot{r}\frac{d\dot{r}}{dr}=h^2/r^3-\frac{\mu}{r^2}$$
$\dot{r}d\dot{r}=(h^2/r^3-\frac{\mu}{r^2})dr$,两端积分
$$\dot{r}^2={2\mu}/r-h^2/r^2+K_1\tag{11}$$$$\Rightarrow {dt}/{dr}=\frac{r}{\sqrt{K_1 r^2+2\mu r-h^2}}$$
$t=\int \frac{r}{\sqrt{K_1 r^2+2\mu r-h^2}}dr$
丘成桐摘得沃尔夫奖——获数学界终身成就肯定
By 苏剑林 | 2010-02-27 | 27988位读者 | 引用1月31日晚,华裔数学家丘成桐收到以色列教育部部长兼沃尔夫基金会理事长Gideon Sa’ar亲笔签名的信,通知他获得了2010年的沃尔夫数学奖,原因是他“在几何分析方面的贡献已对几何和物理的许多领域产生深远而引人瞩目的影响”。
1978年开始颁发的沃尔夫奖每年评选一次,分别奖励在农业、化学、数学、医药、物理以及艺术领域中取得突出成绩的人士。其中沃尔夫数学奖影响很大。
今年的颁奖典礼定于5月13日在耶路撒冷举行,丘成桐将与美国数学家丹尼斯·沙利文分享10万美元的数学奖奖金。这是丘成桐继菲尔茨奖后,再次获得国际最顶尖的数学大奖。菲尔茨奖和沃尔夫奖双奖得主,迄今只有13位。
科学空间:2010年3月重要天象
By 苏剑林 | 2010-02-28 | 23273位读者 | 引用 3月份,大地回暖,春暖花开了,精彩的天象在等着我们。这个月天空的主角无疑是美丽的土星,火星和金星也是较好的观测对象。而且3月又正值梅西叶马拉松的好时节,许多有趣、朦胧的深空天体,无疑会极大地挑起我们对神秘的春夜星空的兴趣。这里有一本《梅西叶马拉松全年指导手册》电子书,新手不妨作为入门的参考书。
3月份,大地回暖,春暖花开了,精彩的天象在等着我们。这个月天空的主角无疑是美丽的土星,火星和金星也是较好的观测对象。而且3月又正值梅西叶马拉松的好时节,许多有趣、朦胧的深空天体,无疑会极大地挑起我们对神秘的春夜星空的兴趣。这里有一本《梅西叶马拉松全年指导手册》电子书,新手不妨作为入门的参考书。
梅西叶马拉松是一个自我挑战性相对较强的活动,因为虽然一夜之间所有的梅西耶天体全都亮相,但是因为升起的时间相差很多,有些天体的角度就很低了,并不十分适宜观测,况且一夜之间观测103个天体,即使对星空和器材性能非常熟悉,也需要相当时间(当然啦,你如果有电动赤道仪和导星输入的话,就很简单拉),这会是一个非常辛苦的活动,需要充分准备。 爱好挑战困难者,上吧,探索我们的宇宙!
问世间质心(重心)知多少
By 苏剑林 | 2010-07-26 | 46424位读者 | 引用【科学松鼠会】猫江湖(科学也是可以很有趣的)
By 苏剑林 | 2010-08-02 | 18929位读者 | 引用不要认为科学是一门多么枯燥、深奥的的学科,只要有点创意,科学也可以有趣起来。这种创意并非来源于专业人员,而是来源于生活,来源于关注 ,来源于一颗好奇而勇敢的心。下面请看科学松鼠会推出的《猫江湖》。
我有一个梦想,这个种群将会觉醒,实现其立群信条的真谛:猫猫生而平等;
我有一个梦想,在食堂垃圾桶边,阉割猫和健全公猫能同席而坐,共叙兄弟情谊;
我有一个梦想,甚至连临时喂食点这个正义匿迹、压迫成风的地方,也将变成平等和自由的绿洲;
我有一个梦想,让天下的猫孩儿都有爸爸,我的四个孩子将在一个不是以他们的毛色,而是以健康优劣作为评判标准的国家里生活;
日出东方,重逢,最美的风采
By 苏剑林 | 2010-08-05 | 21184位读者 | 引用历时三年,经过三届评选,《日出东方》、《重逢》和《最美的风采》入围亚运会会歌候选歌曲。就BoJone而言,比较喜欢的事《日出东方》。最终结果如何?让我们拭目以待!
日出东方,我们在广州重逢,展示最美的风采!
其中,《日出东方》的作曲是知名曲作家李海鹰,作词是朱海。歌曲名字与广州亚运标识五羊上方绚丽的太阳形象完全契合,体现了克服困难取得胜利的体育精神,同时也有亚运火炬薪火相传、永不熄灭的含义。《重逢》的作曲是捞仔,作词是徐荣凯。歌曲取名重逢,突出了亚运会不仅是亚洲的运动盛会,也是亚洲兄弟姐妹四年一次的盛大友谊聚会,亚洲虽然辽阔,但亚洲人民之间的深厚友谊缩短了彼此的距离。《最美的风采》则是由香港著名作曲家金培达作曲,广州知名音乐人陈小奇作词。歌曲将“花海”与“运动会”的意象巧妙地融为一体,彰显出广州作为“花城”及亚运会主办城市所具有的风采,及“和谐亚洲,激情盛会”的主题。












最近评论