7
Oct
两男一女分享2009年诺贝尔化学奖
By 苏剑林 | 2009-10-07 | 18213位读者 | 引用
28
Jun
第114号化学元素再次被实验确认
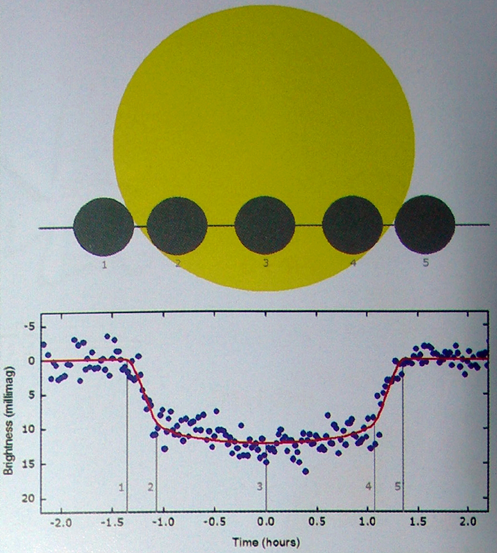
By 苏剑林 | 2010-06-28 | 16520位读者 | 引用
9
Aug
“凌星时刻变化”技术搜寻外行星
By 苏剑林 | 2010-08-09 | 18884位读者 | 引用
6
Oct
2010年诺贝尔化学奖出炉,美日科学家分享
By 苏剑林 | 2010-10-06 | 22087位读者 | 引用
6
Nov
[遐想]细胞的进化是一次次“大吞并”？
By 苏剑林 | 2011-11-06 | 42513位读者 | 引用传说中的高三备考是一次全面系统的大复习，但对于我们而言，它并不是复习，而是学习。我发现很多知识点在以前都是鲜有接触的，这无疑说明了两个问题：当时我学习得很肤浅；我的遗忘力太强了。就拿生物来说吧，以前总是很简单地就跳阅过去了，从不会去思考一些深入的问题。现在的重新“复习”阶段，却饶有兴趣地引出了很多的思考。特别是有关细胞进化的讨论，显得特别有趣。
一个典型的有尾噬菌体的结构：①头部，②尾部，③核酸，④头壳，⑤颈部，⑥尾鞘，⑦尾丝，⑧尾钉，⑨基板
根据古生物的研究，地球上第一个生命起源于32亿年前，是一个很简单的原核细胞，其遗传物质是RNA，后来逐渐演变成以DNA为遗传物质，例如细菌有一个环状的DNA分子。原核生物很快就进化出了真核生物，因为迄今所知最古老的真核生物化石已有近21亿年的历史，许多科学家推测，最早的真核生物可能早在30亿年前就出现了。
这里便引申出了一个问题：病毒是什么时候出现的？它是怎么出现的？
4
Feb
[更新]将向量乘法“退化”到复数
By 苏剑林 | 2011-02-04 | 57725位读者 | 引用向量有两个乘法：点乘和叉乘，其结果又分别叫做数量积和向量积。在很多情况下，用这两个定义的乘法运算都能够给我们带来很大的方便（其实它就是在实际问题中抽象出来的）。不过，也有相当一部分的二维问题用复数来描述更为简洁。于是，为了整合两者的巧妙之处，有必要把向量的两个乘法运算“退化”到复数中去（为什么用“退化”？因为向量是多维的，可以是3维、4维等，而复数运算只是二维的，很明显这是一种“退化”而不是“拓展”^_^）
运算法则：
点乘：
总法则：$Z_1 \cdot Z_2=|Z_1||Z_2|\cos(arg\frac{Z_2}{Z_1})$
$$\begin{aligned}1\cdot i=0 \\ i\cdot i=1 \\ \exp(i\theta)\cdot \exp(i\varphi)=\cos(\varphi -\theta) \\ iexp(i\theta)\cdot \exp(i\varphi)=-\sin(\theta-\varphi ) \\ Z_1 \cdot Z_2=Z_1 \bar{Z}_2+Z_2 \bar{Z}_1\end{aligned}$$
23
Apr
2010年广东省高中学生化学竞赛试题和答案
By 苏剑林 | 2011-04-23 | 22475位读者 | 引用
6
Jul
椭圆内的一根定长弦（化圆法）
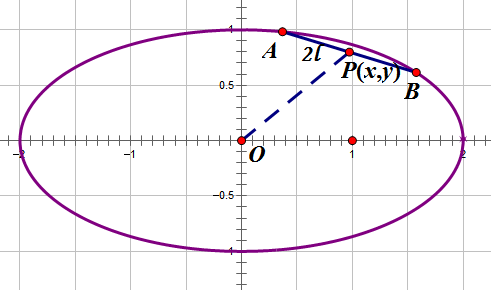
By 苏剑林 | 2012-07-06 | 31150位读者 | 引用在上一篇文章《抛物线内的一根定长弦》中，我们解决了抛物线内的定长弦中点轨迹问题，那还算是一个比较简单的问题。虽然同是圆锥曲线，但把同样的问题延伸到椭圆上，却不是那么简单了。因为椭圆的轨迹方程的x,y坐标通过平方相互“纠缠”在一起，不像抛物线方程那样可以容易分离开来（指的是分离成$y=f(x)$的形式）。BoJone尝试了若干种方法，还是难以把它的轨迹求出来。最后通过“化圆法”，终得轨迹方程。
椭圆内的定长弦1
所谓化圆法，就是将椭圆通过拉伸变成一个圆，利用圆的性质来解决一些问题。众所周知，相比椭圆，圆具有相当多的简单性。这是我高考前研究各种各样的高考圆锥曲线题时，所总结出来的一种方法。有时候，把椭圆拉伸为圆后，结论就相当显然了；同时，圆作为一个特殊的椭圆，椭圆的一般结论，放在圆上自然也是成立的。所以要研究椭圆问题，不妨先研究它的特例——圆问题；另一方面，利用圆的对称性等等，也可以大幅度地减少计算量，所以BoJone很喜欢这个方法。更想不到的是，它居然在求本文的轨迹时派上用场了。
最近评论