端午&高考乱弹:怀念的,也许只是怀念本身
By 苏剑林 | 2019-06-07 | 52468位读者 | 引用漫谈重参数:从正态分布到Gumbel Softmax
By 苏剑林 | 2019-06-10 | 236922位读者 | 引用最近在用VAE处理一些文本问题的时候遇到了对离散形式的后验分布求期望的问题,于是沿着“离散分布 + 重参数”这个思路一直搜索下去,最后搜到了Gumbel Softmax,从对Gumbel Softmax的学习过程中,把重参数的相关内容都捋了一遍,还学到一些梯度估计的新知识,遂记录在此。
文章从连续情形出发开始介绍重参数,主要的例子是正态分布的重参数;然后引入离散分布的重参数,这就涉及到了Gumbel Softmax,包括Gumbel Softmax的一些证明和讨论;最后再讲讲重参数背后的一些故事,这主要跟梯度估计有关。
基本概念
重参数(Reparameterization)实际上是处理如下期望形式的目标函数的一种技巧:
\begin{equation}L_{\theta}=\mathbb{E}_{z\sim p_{\theta}(z)}[f(z)]\label{eq:base}\end{equation}
这样的目标在VAE中会出现,在文本GAN也会出现,在强化学习中也会出现($f(z)$对应于奖励函数),所以深究下去,我们会经常碰到这样的目标函数。取决于$z$的连续性,它对应不同的形式:
\begin{equation}\int p_{\theta}(z) f(z)dz\,\,\,\text{(连续情形)}\qquad\qquad \sum_{z} p_{\theta}(z) f(z)\,\,\,\text{(离散情形)}\end{equation}
当然,离散情况下我们更喜欢将记号$z$换成$y$或者$c$。
最小熵原理(五):“层层递进”之社区发现与聚类
By 苏剑林 | 2019-10-19 | 157263位读者 | 引用让我们不厌其烦地回顾一下:最小熵原理是一个无监督学习的原理,“熵”就是学习成本,而降低学习成本是我们的不懈追求,所以通过“最小化学习成本”就能够无监督地学习出很多符合我们认知的结果,这就是最小熵原理的基本理念。
这篇文章里,我们会介绍一种相当漂亮的聚类算法,它同样也体现了最小熵原理,或者说它可以通过最小熵原理导出来,名为InfoMap,或者MapEquation。事实上InfoMap已经是2007年的成果了,最早的论文是《Maps of random walks on complex networks reveal community structure》,虽然看起来很旧,但我认为它仍是当前最漂亮的聚类算法,因为它不仅告诉了我们“怎么聚类”,更重要的是给了我们一个“为什么要聚类”的优雅的信息论解释,并从这个解释中直接导出了整个聚类过程。
当然,它的定位并不仅仅局限在聚类上,更准确地说,它是一种图网络上的“社区发现”算法。所谓社区发现(Community Detection),大概意思是给定一个有向/无向图网络,然后找出这个网络上的“抱团”情况,至于详细含义,大家可以自行搜索一下。简单来说,它跟聚类相似,但是比聚类的含义更丰富。(还可以参考《什么是社区发现?》)
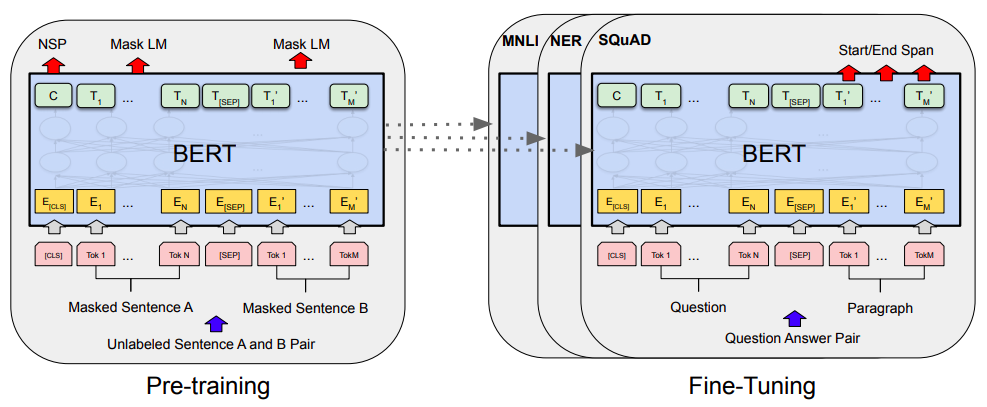
当Bert遇上Keras:这可能是Bert最简单的打开姿势
By 苏剑林 | 2019-06-18 | 432739位读者 | 引用Bert是什么,估计也不用笔者来诸多介绍了。虽然笔者不是很喜欢Bert,但不得不说,Bert确实在NLP界引起了一阵轩然大波。现在不管是中文还是英文,关于Bert的科普和解读已经满天飞了,隐隐已经超过了当年Word2Vec刚出来的势头了。有意思的是,Bert是Google搞出来的,当年的word2vec也是Google搞出来的,不管你用哪个,都是在跟着Google大佬的屁股跑啊~
Bert刚出来不久,就有读者建议我写个解读,但我终究还是没有写。一来,Bert的解读已经不少了,二来其实Bert也就是基于Attention的搞出来的大规模语料预训练的模型,本身在技术上不算什么创新,而关于Google的Attention我已经写过解读了,所以就提不起劲来写了。
总的来说,我个人对Bert一直也没啥兴趣,直到上个月末在做信息抽取比赛时,才首次尝试了Bert。因为后来想到,即使不感兴趣,终究也是得学会它,毕竟用不用是一回事,会不会又是另一回事。再加上在Keras中使用(fine tune)Bert,似乎还没有什么文章介绍,所以就分享一下自己的使用经验。
“让Keras更酷一些!”:层与模型的重用技巧
By 苏剑林 | 2019-09-29 | 113672位读者 | 引用今天我们继续来深挖Keras,再次体验Keras那无与伦比的优雅设计。这一次我们的焦点是“重用”,主要是层与模型的重复使用。
所谓重用,一般就是奔着两个目标去:一是为了共享权重,也就是说要两个层不仅作用一样,还要共享权重,同步更新;二是避免重写代码,比如我们已经搭建好了一个模型,然后我们想拆解这个模型,构建一些子模型等。
基础
事实上,Keras已经为我们考虑好了很多,所以很多情况下,掌握好基本用法,就已经能满足我们很多需求了。
层的重用
层的重用是最简单的,将层初始化好,存起来,然后反复调用即可:
x_in = Input(shape=(784,))
x = x_in
layer = Dense(784, activation='relu') # 初始化一个层,并存起来
x = layer(x) # 第一次调用
x = layer(x) # 再次调用
x = layer(x) # 再次调用6个派生优化器的简单介绍及其实现
By 苏剑林 | 2019-11-25 | 53412位读者 | 引用优化器可能是深度学习最“玄学”的一个模块之一了:有时候换一个优化器就能带来明显的提升,有时候别人说提升很多的优化器用到自己的任务上却一丁点用都没有,理论性质好的优化器不一定工作得很好,纯粹拍脑袋而来的优化器也未必就差了。但不管怎样,优化器终究也为热爱“深度炼丹”的同学提供了多一个选择。
近几年来,关于优化器的工作似乎也在慢慢增多,很多论文都提出了对常用优化器(尤其是Adam)的大大小小的改进。本文就汇总一些优化器工作或技巧,并统一给出了代码实现,供读者有需调用。
基本形式
所谓“派生”,就是指相关的技巧都是建立在已有的优化器上的,任意一个已有的优化器都可以用上这些技巧,从而变成一个新的优化器。
已有的优化器的基本形式为:
\begin{equation}\begin{aligned}\boldsymbol{g}_t =&\, \nabla_{\boldsymbol{\theta}} L\\
\boldsymbol{h}_t =&\, f(\boldsymbol{g}_{\leq t})\\
\boldsymbol{\theta}_{t+1} =&\, \boldsymbol{\theta}_t - \gamma \boldsymbol{h}_t
\end{aligned}\end{equation}
其中$\boldsymbol{g}_t$即梯度,而$\boldsymbol{g}_{\leq t}$指的是截止到当前步的所有梯度信息,它们经过某种运算$f$(比如累积动量、累积二阶矩校正学习率等)后得到$\boldsymbol{h}_t$,然后由$\boldsymbol{h}_t$来更新参数,这里的$\gamma$就是指学习率。
基于Bert的NL2SQL模型:一个简明的Baseline
By 苏剑林 | 2019-06-29 | 145050位读者 | 引用在之前的文章《当Bert遇上Keras:这可能是Bert最简单的打开姿势》中,我们介绍了基于微调Bert的三个NLP例子,算是体验了一把Bert的强大和Keras的便捷。而在这篇文章中,我们再添一个例子:基于Bert的NL2SQL模型。
NL2SQL的NL也就是Natural Language,所以NL2SQL的意思就是“自然语言转SQL语句”,近年来也颇多研究,它算是人工智能领域中比较实用的一个任务。而笔者做这个模型的契机,则是今年我司举办的首届“中文NL2SQL挑战赛”:
首届中文NL2SQL挑战赛,使用金融以及通用领域的表格数据作为数据源,提供在此基础上标注的自然语言与SQL语句的匹配对,希望选手可以利用数据训练出可以准确转换自然语言到SQL的模型。
这个NL2SQL比赛算是今年比较大型的NLP赛事了,赛前投入了颇多人力物力进行宣传推广,比赛的奖金也颇丰富,唯一的问题是NL2SQL本身算是偏冷门的研究领域,所以注定不会太火爆,为此主办方也放出了一个Baseline,基于Pytorch写的,希望能降低大家的入门难度。
抱着“Baseline怎么能少得了Keras版”的心态,我抽时间自己用Keras做了做这个比赛,为了简化模型并且提升效果也加载了预训练的Bert模型,最终形成此文。








最近评论