科学空间|Scientific Spaces

前段时间写了《万能的seq2seq：基于seq2seq的阅读理解问答》，探索了以最通用的seq2seq的方式来做阅读理解式问答，并且取得相当不错的成绩（单模型0.77，超过参加比赛时精调的最佳模型）。这篇文章我们继续做这个任务，不过换一个思路，直接基于MLM模型来做，最终成绩基本一致，但能提高预测速度。

用MLM做阅读理解的模型图示（其中[M]表示[MASK]标记）

点击阅读全文...

分享个人实现的bert4keras：

https://github.com/bojone/bert4keras

这是笔者重新实现的keras版的bert，致力于用尽可能清爽的代码来实现keras下调用bert。

说明

目前已经基本实现bert，并且能成功加载官方权重，经验证模型输出跟keras-bert一致，大家可以放心使用。

本项目的初衷是为了修改、定制上的方便，所以可能会频繁更新。

因此欢迎star，但不建议fork，因为你fork下来的版本可能很快就过期了。

点击阅读全文...

印象中很早之前就看到过VQ-VAE，当时对它并没有什么兴趣，而最近有两件事情重新引起了我对它的兴趣。一是VQ-VAE-2实现了能够匹配BigGAN的生成效果（来自机器之心的报道）；二是我最近看一篇NLP论文《Unsupervised Paraphrasing without Translation》时发现里边也用到了VQ-VAE。这两件事情表明VQ-VAE应该是一个颇为通用和有意思的模型，所以我决定好好读读它。

个人复现的VQ-VAE在CelebA上的重构效果。可以留意到细节保留得还不错，但稍微放大后能留意到仍有一些模糊感。

点击阅读全文...

在我看来，几大顶会之中，ICLR的论文通常是最有意思的，因为它们的选题和风格基本上都比较轻松活泼、天马行空，让人有脑洞大开之感。所以，ICLR 2020的投稿论文列表出来之后，我也抽时间粗略过了一下这些论文，确实发现了不少有意思的工作。

其中，我发现了两篇利用去噪自编码器的思想做生成模型的论文，分别是《Learning Generative Models using Denoising Density Estimators》和《Annealed Denoising Score Matching: Learning Energy-Based Models in High-Dimensional Spaces》。由于常规做生成模型的思路我基本都有所了解，所以这种“别具一格”的思路就引起了我的兴趣。细读之下，发现两者的出发点是一致的，但是具体做法又有所不同，最终的落脚点又是一样的，颇有“一题多解”的美妙，遂将这两篇论文放在一起，对比分析一翻。

fashion mnist、CelebA、cifar10上的生成效果

点击阅读全文...

生成模型一直是笔者比较关注的主题，不管是NLP和CV的生成模型都是如此。这篇文章里，我们介绍一个新颖的生成模型，来自论文《Batch norm with entropic regularization turns deterministic autoencoders into generative models》，论文中称之为EAE（Entropic AutoEncoder）。它要做的事情给变分自编码器（VAE）基本一致，最终效果其实也差不多（略优），说它新颖并不是它生成效果有多好，而是思路上的新奇，颇有别致感。此外，借着这个机会，我们还将学习一种统计量的估计方法——$k$邻近方法，这是一种很有用的非参数估计方法。

自编码器vs生成模型

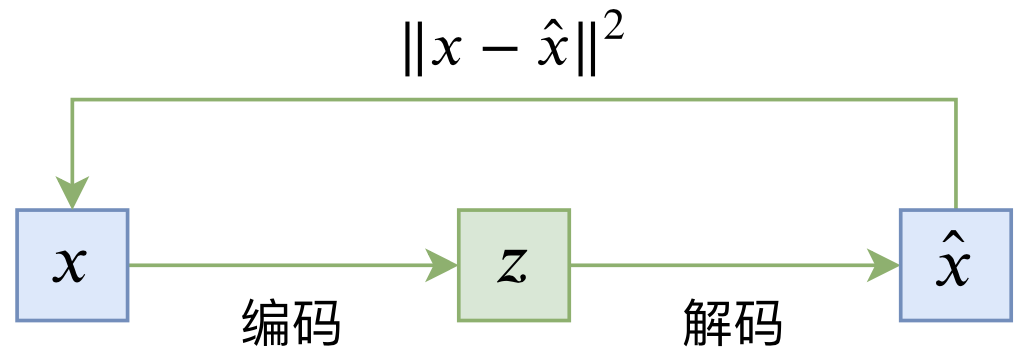
普通的自编码器是一个“编码-解码”的重构过程，如下图所示：

典型自编码器示意图

其loss一般为
\begin{equation}L_{AE} = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - \hat{x}\right\Vert^2\right] = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - D(E(x))\right\Vert^2\right]\end{equation}

点击阅读全文...

前段时间公司组织技术分享，轮到笔者时，大家希望我讲讲VAE。鉴于之前笔者也写过变分自编码器系列，所以对笔者来说应该也不是特别难的事情，因此就答应了下来，后来仔细一想才觉得犯难：怎么讲才好呢？

变分自编码器示意图

对于VAE来说，之前笔者有两篇比较系统的介绍：《变分自编码器（一）：原来是这么一回事》和《变分自编码器（二）：从贝叶斯观点出发》。后者是纯概率推导，对于不做理论研究的人来说其实没什么意义，也不一定能看得懂；前者虽然显浅一点，但也不妥，因为它是从生成模型的角度来讲的，并没有说清楚“为什么需要VAE”（说白了，VAE可以带来生成模型，但是VAE并不一定就为了生成模型），整体风格也不是特别友好。

笔者想了想，对于大多数不了解但是想用VAE的读者来说，他们应该只希望大概了解VAE的形式，然后想要知道“VAE有什么作用”、“VAE相比AE有什么区别”、“什么场景下需要VAE”等问题的答案，对于这种需求，上面两篇文章都无法很好地满足。于是笔者尝试构思了VAE的一种几何图景，试图从几何角度来描绘VAE的关键特性，在此也跟大家分享一下。

点击阅读全文...

在之前的文章《必须要GPT3吗？不，BERT的MLM模型也能小样本学习》中，我们介绍了一种名为Pattern-Exploiting Training（PET）的方法，它通过人工构建的模版与BERT的MLM模型结合，能够起到非常好的零样本、小样本乃至半监督学习效果，而且该思路比较优雅漂亮，因为它将预训练任务和下游任务统一起来了。然而，人工构建这样的模版有时候也是比较困难的，而且不同的模版效果差别也很大，如果能够通过少量样本来自动构建模版，也是非常有价值的。

P-tuning直接使用[unused]来构建模版，不关心模版的自然语言性

最近Arxiv上的论文《GPT Understands, Too》提出了名为P-tuning的方法，成功地实现了模版的自动构建。不仅如此，借助P-tuning，GPT在SuperGLUE上的成绩首次超过了同等级别的BERT模型，这颠覆了一直以来“GPT不擅长NLU”的结论，也是该论文命名的缘由。

点击阅读全文...

在《变分自编码器（五）：VAE + BN = 更好的VAE》中，我们讲到了NLP中训练VAE时常见的KL散度消失现象，并且提到了通过BN来使得KL散度项有一个正的下界，从而保证KL散度项不会消失。事实上，早在2018年的时候，就有类似思想的工作就被提出了，它们是通过在VAE中改用新的先验分布和后验分布，来使得KL散度项有一个正的下界。

该思路出现在2018年的两篇相近的论文中，分别是《Hyperspherical Variational Auto-Encoders》和《Spherical Latent Spaces for Stable Variational Autoencoders》，它们都是用定义在超球面的von Mises–Fisher（vMF）分布来构建先后验分布。某种程度上来说，该分布比我们常用的高斯分布还更简单和有趣～

KL散度消失

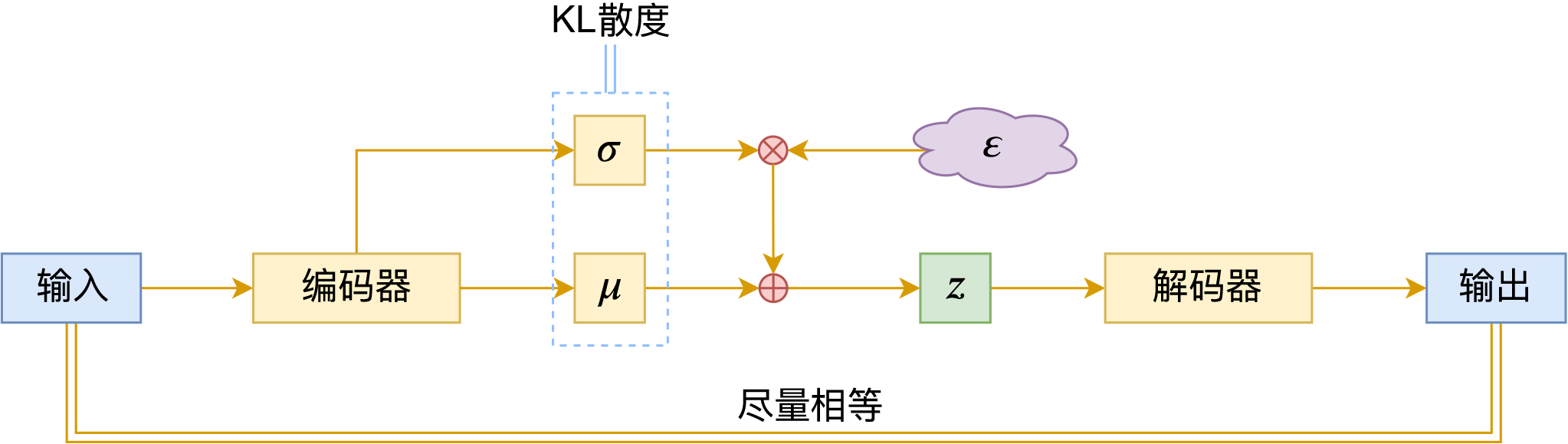
我们知道，VAE的训练目标是
\begin{equation}\mathcal{L} = \mathbb{E}_{x\sim \tilde{p}(x)} \Big[\mathbb{E}_{z\sim p(z|x)}\big[-\log q(x|z)\big]+KL\big(p(z|x)\big\Vert q(z)\big)\Big]
\end{equation}

点击阅读全文...