科学空间|Scientific Spaces

本章将路径积分用于随机微分方程，并且得到了与不对称随机游走一样的结果，从而证明了它与该模型的等价性.

将路径积分用于随机微分方程的研究，这一思路由来已久. 费曼在他的著作[5]中，已经建立了路径积分与线性随机微分方程的关系. 而对于非线性的情况，也有不少研究，但比较混乱，如文献[8]甚至给出了错误的结果.

本文从路径积分的离散化概念出发，明确地建立了两个路径积分微元的雅可比行列式关系，从而对非线性随机微分方程也建立了路径积分. 本文的结果跟文献[9]的结果是一致的.

概念

本文所研究的仅仅是随机常微分方程，它与一般的常微分方程的区别在于布朗运动项的引入，如常见的一类随机微分方程为
$$dx(t)=p(x(t),t)dt + \sqrt{\alpha} dW_t.\tag{48}$$
其中$W_t$代表着一个标准的布朗运动. 由于引入了随机项，所以解$x(t)$不再是确定的，而是有一定的概率分布.

在对随机微分方程中，感兴趣的量有很多，比如关于$x$的某个量的期望、方差，或者稳定性，等等. 随机微分方程领域中有各种分析的技巧，但是显然，直接求出$x(t)$的概率分布后对概率分布进行研究，是最理想最容易的方案. 路径积分正是给出了求概率分布的一个方法.

点击阅读全文...

经过第一部分，我们已经较好地提取了图像的文本特征，下面进行文字定位. 主要过程分两步：1、邻近搜索，目的是圈出单行文字；2、文本切割，目的是将单行文本切割为单字.

邻近搜索

我们可以对提取的特征图进行连通区域搜索，得到的每个连通区域视为一个汉字. 这对于大多数汉字来说是适用，但是对于一些比较简单的汉字却不适用，比如“小”、“旦”、“八”、“元”这些字，由于不具有连通性，所以就被分拆开了，如图13. 因此，我们需要通过邻近搜索算法，来整合可能成字的区域，得到单行的文本区域.

图13 直接搜索连通区域，会把诸如“元”之类的字分拆开

邻近搜索的目的是进行膨胀，以把可能成字的区域“粘合”起来. 如果不进行搜索就膨胀，那么膨胀是各个方向同时进行的，这样有可能把上下行都粘合起来了. 因此，我们只允许区域向单一的一个方向膨胀. 我们正是要通过搜索邻近区域来确定膨胀方向(上、下、左、右)：

邻近搜索* 从一个连通区域出发，可以找到该连通区域的水平外切矩形，将连通区域扩展到整个矩形. 当该区域与最邻近区域的距离小于一定范围时，考虑这个矩形的膨胀，膨胀的方向是最邻近区域的所在方向.

既然涉及到了邻近，那么就需要有距离的概念. 下面给出一个比较合理的距离的定义.

距离

图14 两个示例区域

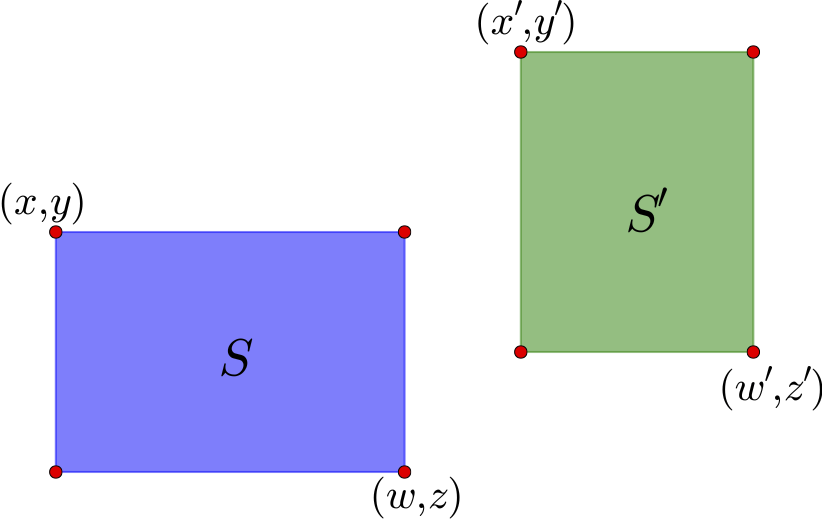
如上图，通过左上角坐标$(x,y)$和右下角坐标$(z,w)$就可以确定一个矩形区域，这里的坐标是以左上角为原点来算的. 这个区域的中心是$\left(\frac{x+w}{2},\frac{y+z}{2}\right)$. 对于图中的两个区域$S$和$S'$，可以计算它们的中心向量差
$$(x_c,y_c)=\left(\frac{x'+w'}{2}-\frac{x+w}{2},\frac{y'+z'}{2}-\frac{y+z}{2}\right)\tag{10}$$
如果直接使用$\sqrt{x_c^2+y_c^2}$作为距离是不合理的，因为这里的邻近应该是按边界来算，而不是中心点. 因此，需要减去区域的长度：
$$(x'_c,y'_c)=\left(x_c-\frac{w-x}{2}-\frac{w'-x'}{2},y_c-\frac{z-y}{2}-\frac{z'-y'}{2}\right)\tag{11}$$
距离定义为
$$d(S,S')=\sqrt{[\max(x'_c,0)]^2+[\max(y'_c,0)]^2}\tag{12}$$
至于方向，由$(x_c,y_c)$的幅角进行判断即可.

然而，按照前面的“邻近搜索*”方法，容易把上下两行文字粘合起来，因此，基于我们的横向排版假设，更好的方法是只允许横向膨胀：

邻近搜索 从一个连通区域出发，可以找到该连通区域的水平外切矩形，将连通区域扩展到整个矩形. 当该区域与最邻近区域的距离小于一定范围时，考虑这个矩形的膨胀，膨胀的方向是最邻近区域的所在方向，当且仅当所在方向是水平的，才执行膨胀操作.

结果

有了距离之后，我们就可以计算每两个连通区域之间的距离，然后找出最邻近的区域. 我们将每个区域向它最邻近的区域所在的方向扩大4分之一，这样邻近的区域就有可能融合为一个新的区域，从而把碎片整合.

实验表明，邻近搜索的思路能够有效地整合文字碎片，结果如图15.

图15 通过邻近搜索后，圈出的文字区域

去年泰迪杯竞赛过后，笔者写了一篇简要介绍深度学习在情感分析中的应用的博文《文本情感分类（二）：深度学习模型》。虽然文章很粗糙，但还是得到了不少读者的反响，让我颇为意外。然而，那篇文章中在实现上有些不清楚的地方，这是因为：1、在那篇文章以后，keras已经做了比较大的改动，原来的代码不通用了；2、里边的代码可能经过我随手改动过，所以发出来的时候不是最适当的版本。因此，在近一年之后，我再重拾这个话题，并且完成一些之前没有完成的测试。

为什么要用深度学习模型？除了它更高精度等原因之外，还有一个重要原因，那就是它是目前唯一的能够实现“端到端”的模型。所谓“端到端”，就是能够直接将原始数据和标签输入，然后让模型自己完成一切过程——包括特征的提取、模型的学习。而回顾我们做中文情感分类的过程，一般都是“分词——词向量——句向量(LSTM)——分类”这么几个步骤。虽然很多时候这种模型已经达到了state of art的效果，但是有些疑问还是需要进一步测试解决的。对于中文来说，字才是最低粒度的文字单位，因此从“端到端”的角度来看，应该将直接将句子以字的方式进行输入，而不是先将句子分好词。那到底有没有分词的必要性呢？本文测试比较了字one hot、字向量、词向量三者之间的效果。

模型测试

本文测试了三个模型，或者说，是三套框架，具体代码在文末给出。这三套框架分别是：

1、one hot：以字为单位，不分词，将每个句子截断为200字（不够则补空字符串），然后将句子以“字-one hot”的矩阵形式输入到LSTM模型中进行学习分类；

2、one embedding：以字为单位，不分词，，将每个句子截断为200字（不够则补空字符串），然后将句子以“字-字向量(embedding)“的矩阵形式输入到LSTM模型中进行学习分类；

3、word embedding：以词为单位，分词，，将每个句子截断为100词（不够则补空字符串），然后将句子以“词-词向量(embedding)”的矩阵形式输入到LSTM模型中进行学习分类。

点击阅读全文...

文件说明：

1. image.py——图像处理函数，主要是特征提取；

2. model_training.py——训练CNN单字识别模型（需要较高性能的服务器，最好有GPU加速，否则真是慢得要死）；

3. ocr.py——识别函数，包括单字分割、前面训练好的模型进行单字识别、动态规划提升效果；

4. main.py——主文件，用来调用1、3两个文件。

5、我们的模型中包含的字.txt(UTF-8编码)

点击阅读全文...

前言：这个暑假花了不少时间在中文分词和语言模型上面，碰了无数次壁，也得到了零星收获。打算写一个专题，分享一下心得体会。虽说是专题，但仅仅是一些笔记式的集合，并非系统的教程，请读者见谅。

中文分词

关于中文分词的介绍和重要性，我就不多说了，matrix67这里有一篇关于分词和分词算法很清晰的介绍，值得一读。在文本挖掘中，虽然已经有不少文章探索了不分词的处理方法，如本博客的《文本情感分类（三）：分词 OR 不分词》，但在一般场合都会将分词作为文本挖掘的第一步，因此，一个有效的分词算法是很重要的。当然，中文分词作为第一步，已经被探索很久了，目前做的很多工作，都是总结性质的，最多是微弱的改进，并不会有很大的变化了。

目前中文分词主要有两种思路：查词典和字标注。首先，查词典的方法有：机械的最大匹配法、最少词数法，以及基于有向无环图的最大概率组合，还有基于语言模型的最大概率组合，等等。查词典的方法简单高效（得益于动态规划的思想），尤其是结合了语言模型的最大概率法，能够很好地解决歧义问题，但对于中文分词一大难度——未登录词（中文分词有两大难度：歧义和未登录词），则无法解决；为此，人们也提出了基于字标注的思路，所谓字标注，就是通过几个标记（比如4标注的是：single，单字成词；begin，多字词的开头；middle，三字以上词语的中间部分；end，多字词的结尾），把句子的正确分词法表示出来。这是一个序列（输入句子）到序列（标记序列）的过程，能够较好地解决未登录词的问题，但速度较慢，而且对于已经有了完备词典的场景下，字标注的分词效果可能也不如查词典方法。总之，各有优缺点（似乎是废话～），实际使用可能会结合两者，像结巴分词，用的是有向无环图的最大概率组合，而对于连续的单字，则使用字标注的HMM模型来识别。

点击阅读全文...

暑假期间做了一下百度和西安交大联合举办的核心实体识别竞赛，最终的结果还不错，遂记录一下。模型的效果不是最好的，但是胜在“端到端”，迁移性强，估计对大家会有一定的参考价值。

比赛的主题是“核心实体识别”，其实有两个任务：核心识别 + 实体识别。这两个任务虽然有关联，但在传统自然语言处理程序中，一般是将它们分开处理的，而这次需要将两个任务联合在一起。如果只看“核心识别”，那就是传统的关键词抽取任务了，不同的是，传统的纯粹基于统计的思路（如TF-IDF抽取）是行不通的，因为单句中的核心实体可能就只出现一次，这时候统计估计是不可靠的，最好能够从语义的角度来理解。我一开始就是从“核心识别”入手，使用的方法类似QA系统：

1、将句子分词，然后用Word2Vec训练词向量；

2、用卷积神经网络（在这种抽取式问题上，CNN效果往往比RNN要好）卷积一下，得到一个与词向量维度一样的输出；

3、损失函数就是输出向量跟训练样本的核心词向量的cos值。

点击阅读全文...

迄今为止，前四篇文章已经介绍了分词的若干思路，其中有基于最大概率的查词典方法、基于HMM或LSTM的字标注方法等。这些都是已有的研究方法了，笔者所做的就只是总结工作而已。查词典方法和字标注各有各的好处，我一直在想，能不能给出一种只需要大规模语料来训练的无监督分词模型呢？也就是说，怎么切分，应该是由语料来决定的，跟语言本身没关系。说白了，只要足够多语料，就可以告诉我们怎么分词。

看上去很完美，可是怎么做到呢？《2.基于切分的新词发现》中提供了一种思路，但是不够彻底。那里居于切分的新词发现方法确实可以看成一种无监督分词思路，它就是用一个简单的凝固度来判断某处该不该切分。但从分词的角度来看，这样的分词系统未免太过粗糙了。因此，我一直想着怎么提高这个精度，前期得到了一些有意义的结果，但都没有得到一个完整的理论。而最近正好把这个思路补全了。因为没有查找到类似的工作，所以这算是笔者在分词方面的一点原创工作了。

语言模型

首先简单谈一下语言模型。

点击阅读全文...

终于开始谈到重点了，就是这部分内容促使我学习外微分的。用外微分可以方便地推导微分几何的一些内容，有时候还能方便计算。其主要根源在于：外微分本身在形式上是微分的推广，因此微分几何的东西能够使用外微分来描述并不出奇；然后，最重要的原因是，外微分把$dx^{\mu}$看成一组基，因此相当于在几何中引入了两组基，一组是本身的向量基（用张量的语言，就是逆变向量的基），这组基可以做对称的内积，另外一组基就是$dx^{\mu}$，这组基可以做反对称的外积。因此，当外微分引入几何时，微分几何就拥有了微分、积分、对称积、反对称积等各种“理想装备”，这就是外微分能够加速微分几何推导的主要原因。

标架的运动

前面已经得到
$$\begin{aligned}&\omega^{\mu}=h_{\alpha}^{\mu}dx^{\alpha}\\
&d\boldsymbol{r}=\hat{\boldsymbol{e}}_{\mu} \omega^{\mu}\\
&ds^2 = \eta_{\mu\nu} \omega^{\mu}\omega^{\nu}\\
&\langle \hat{\boldsymbol{e}}_{\mu}, \hat{\boldsymbol{e}}_{\nu}\rangle = \eta_{\mu\nu}\end{aligned} \tag{45} $$

点击阅读全文...