科学空间|Scientific Spaces

最近一直在考虑一些自然语言处理问题和一些非线性分析问题，无暇总结发文，在此表示抱歉。本文要说的是对于一阶非线性差分方程（当然高阶也可以类似地做）的一种摄动格式，理论上来说，本方法可以得到任意一阶非线性差分方程的显式渐近解。

非线性差分方程

对于一般的一阶非线性差分方程
$$\begin{equation}\label{chafenfangcheng}x_{n+1}-x_n = f(x_n)\end{equation}$$
通常来说，差分方程很少有解析解，因此要通过渐近分析等手段来分析非线性差分方程的性质。很多时候，我们首先会考虑将差分替换为求导，得到微分方程
$$\begin{equation}\label{weifenfangcheng}\frac{dx}{dn}=f(x)\end{equation}$$
作为差分方程$\eqref{chafenfangcheng}$的近似。其中的原因，除了微分方程有比较简单的显式解之外，另一重要原因是微分方程$\eqref{weifenfangcheng}$近似保留了差分方程$\eqref{chafenfangcheng}$的一些比较重要的性质，如渐近性。例如，考虑离散的阻滞增长模型：
$$\begin{equation}\label{zuzhizengzhang}x_{n+1}=(1+\alpha)x_n -\beta x_n^2\end{equation}$$
对应的微分方程为（差分替换为求导）：
$$\begin{equation}\frac{dx}{dn}=\alpha x -\beta x^2\end{equation}$$
此方程解得
$$\begin{equation}x_n = \frac{\alpha}{\beta+c e^{-\alpha n}}\end{equation}$$
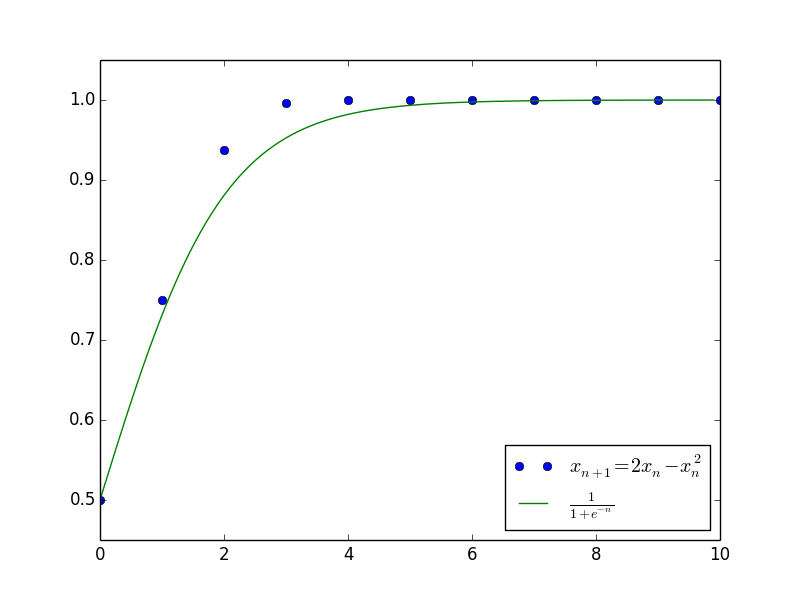
其中$c$是任意常数。上述结果已经大概给出了原差分方程$\eqref{zuzhizengzhang}$的解的变化趋势，并且成功给出了最终的渐近极限$x_n \to \frac{\alpha}{\beta}$。下图是当$\alpha=\beta=1$且$c=1$（即$x_0=\frac{1}{2}$）时，微分方程的解与差分方程的解的值比较。

差分方程的摄动法1

现在的问题是，既然微分方程的解可以作为一个形态良好的近似解了，那么是否可以在微分方程的解的基础上，进一步加入修正项提高精度？

点击阅读全文...

熵的概念

作为一名物理爱好者，我一直对统计力学中“熵”这个概念感到神秘和好奇。因此，当我接触数据科学的时候，我也对最大熵模型产生了浓厚的兴趣。

熵是什么？在通俗的介绍中，熵一般有两种解释：（1）熵是不确定性的度量；（2）熵是信息的度量。看上去说的不是一回事，其实它们说的就是同一个意思。首先，熵是不确定性的度量，它衡量着我们对某个事物的“无知程度”。熵为什么又是信息的度量呢？既然熵代表了我们对事物的无知，那么当我们从“无知”到“完全认识”这个过程中，就会获得一定的信息量，我们开始越无知，那么到达“完全认识”时，获得的信息量就越大，因此，作为不确定性的度量的熵，也可以看作是信息的度量，说准确点，是我们能从中获得的最大的信息量。

点击阅读全文...

众所周知，校园网最宝贵的资源应该有两样：一是IPv6，IPv6是访问Google等网站的最理想途径，当然IPv6并非所有高校都有；二是论文库，一般高校都会买了一部分论文库（知网、万方等）的下载权，供校园用户使用。如果说访问Google还有VPN等诸多方式的话，那么对于校外用户来说访问知网等资源就显得格外宝贵了，一般只是叫校内用户下载，或者就只能付费了（那个贵呀！）。

站长还是学生，在学校同时享用着IPv6和论文库资源，确实很爽。自从用上Openwrt的路由之后，一直想着怎么把校园网资源共享出去。曾经考虑过搭建PPTP VPN，但是感觉略有复杂（当然，跟其他VPN相比，搭建PPTP VPN算是非常简单的了，可是我还是不怎么喜欢。），而且当时还没解决内网穿透的问题。最近借助ssh反向代理的方式实现了内网穿透，继而认识到，通过ssh动态端口转发，居然还可以搭建代理，并且实现远程访问内网（校园网）资源，而且几乎不用在路由器本身上面做任何配置。不得不说，ssh真是一个极其强大的东西呀。

添加普通帐号

既然要共享，就没理由把root账户都分享出去了，因此，第一步要实现的是在Openwrt上添加一个代理账号，而且为了安全和保密，这个账号不允许真的登陆服务器进行操作，而只允许进行端口转发。

点击阅读全文...

说在前面

美食（图片来源于互联网）

在空间侧边栏的笔者的自我介绍中，有一行是“厨房爱好者”，虽然笔者不怎么会做菜，但确实，厨房是我的一个爱好。当然，笔者的爱好很多，数学、物理、天文、计算机等，都喜欢，都想学，弄到多而不精。在之前的文章中也已经提到过，数据挖掘也是我的一个爱好，而当数据挖掘跟厨房这两个爱好相遇了，会有什么有趣的结果吗？

笔者正是做了这样一个事情：从美食中国的家常菜目录下面，写了个简单的爬虫，抓取了一批菜谱数据下来，进行简单的数据分析。（在此对美食中国表示衷心感谢。选择美食中国的原因是它的数据比较规范。）数据分析在我目前公司的高性能服务器做，分析起来特别舒服～～

这里共收集了18209个菜谱，共包含了9700种食材（包括主料、辅料、调料，部分可能由于命名不规范等原因会重复）。当然，这个数据量相对于很多领域的大数据标准来说，实在不值一提。但是在大数据极少涉及的厨房，应该算是比较多的了。

点击阅读全文...

最近在算路径积分的时候，频繁地遇到了以下两种无穷级数：
$$\sum_n \frac{1}{n^2\pm\omega^2}\quad \text{和} \quad \prod_n \left(1\pm\frac{\omega^2}{n^2}\right)$$
当然，直接用Mathematica可以很干脆地算出结果来，但是我还是想知道为什么，至少大概地知道。

伯努利级数

当$\omega=0$的时候，第一个级数变为著名的伯努利级数
$$\sum_n \frac{1}{n^2}=1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\dots$$
既然跟伯努利级数有关，那么很自然想到，从伯努利级数的求和入手。

点击阅读全文...

问题来源

笔者经常学习的数学研发论坛曾有一帖讨论下述非线性差分方程的渐近求解：
$$a_{n+1}=a_n+\frac{1}{a_n^2},\, a_1=1$$
原帖子在这里，从这帖子中我获益良多，学习到了很多新技巧。主要思路是通过将两边立方，然后设$x_n=a_n^3$，变为等价的递推问题：
$$x_{n+1}=x_n+3+\frac{3}{x_n}+\frac{1}{x_n^2},\,x_1=1$$
然后可以通过巧妙的技巧得到渐近展开式：
$$x_n = 3n+\ln n+a+\frac{\frac{1}{3}(\ln n+a)-\frac{5}{18}}{n}+\dots$$
具体过程就不提了，读者可以自行到上述帖子学习。

然而，这种形式的解虽然精妙，但存在一些笔者不是很满意的地方：

1、解是渐近的级数，这就意味着实际上收敛半径为0；
2、是$n^{-k}$形式的解，对于较小的$n$难以计算，这都使得高精度计算变得比较困难；
3、当然，题目本来的目的是渐近计算，但是渐近分析似乎又没有必要展开那么多项；
4、里边带有了一个本来就比较难计算的极限值$a$；
5、求解过程似乎稍欠直观。

当然，上面这些缺点，有些是鸡蛋里挑骨头的。不过，也正是这些缺点，促使我寻找更好的形式的解，最终导致了这篇文章。

点击阅读全文...

我不是研究引力的，也没有很好地学习过引力。在理论物理方面，我学习经典力学和量子力学比学习广义相对论要多得多。因此，本来我是不应该谈引力的，以免误人子弟。不过，在一次坐车的途中，司机的刹车和加速让我联想到了一些跟引力有关的东西，自我感觉比较有趣，所以发给大家分享一下，也请大家指正。

等效原理

坐汽车

引力，准确来说应该是“万有引力”。所谓“万有”，有两个含义：1、所有物体都能够产生引力；2、所有物体都被引力影响。一个力居然是“万有”的，这让爱因斯坦感觉到非常奇怪，这也是四种基本力之中，引力跟其他力区别最明显的地方。相比之下，电磁相互作用力就只能存在于有“电”的地方，弱相互作用只存在于费米子，等等。

除了引力之外，我们平时还遇到过什么“万有”的力吗？貌似没有。但是我们想象一下，当你坐在一辆长途大巴匀速前进时，突然司机来了一个急刹车，在刹车的那一瞬间，所有人都往前倾了，不仅如此，可能你的行李箱、你的随身物品都往前移的，事实上，车上所有东西都受到了一个往前的力！对于那辆车上的人和物来说，刹车的那一瞬间，就存在着一个“万有”的力！

点击阅读全文...

上一篇博文的发布时间是4月15日，到今天刚好一个月没更新了，但是科学空间的访问量还在。感谢大家对本空间的支持，BoJone对久未更新表示非常抱歉。在恢复更新之前，请允许笔者记记流水账。

在“消失”的一个月中，笔者主要的事情是毕业论文和数据挖掘竞赛。首先毕业论文方面，论文于4月22日交稿，4月29日答辩，答辩完后就意味着毕业论文的事情结束了。我的毕业论文主要写了路径积分在描述随机游走、偏微分方程、随机微分方程的应用。既然是本科论文，就不能说得太晦涩，因此论文整体来看还是比较易读的，可以作为路径积分的入门教程。后面我会略加修改，分开几部分发布在科学空间中的，到时请大家批评指正。

说到路径积分，不得不说到做《量子力学与路径积分》的习题解答这件事情了。很遗憾，这一个多月来，基本没有时间做习题。不过后面我会继续做下去的，已发布的版本，也请有兴趣的读者指出问题。记得年初的时候，朋友问我今年的愿望是什么，我随意地回答了“希望做完一本书的习题”，这本书，当然就是《量子力学与路径积分》了，我相信今年应该能够完成的。

点击阅读全文...