科学空间|Scientific Spaces

当要求函数的最小值时，我们通常会先求导函数然后寻找其零点，比较幸运的情况下，这些零点之一正好是原函数的最小值点。如果是向量函数，则将导数改为梯度并求其零点。当梯度零点不易求得时，我们可以使用梯度下降来逐渐逼近最小值点。

以上这些都是无约束优化的基础结果，相信不少读者都有所了解。然而，本文的主题是概率空间中的优化，即目标函数的输入是一个概率分布，这类目标的优化更为复杂，因为它的搜索空间不再是无约束的，如果我们依旧去求解梯度零点或者执行梯度下降，所得结果未必能保证是一个概率分布。因此，我们需要寻找一种新的分析和计算方法，以确保优化结果能够符合概率分布的特性。

对此，笔者一直以来也感到颇为头疼，所以近来决定”痛定思痛“，针对概率分布的优化问题系统学习了一番，最后将学习所得整理在此，供大家参考。

点击阅读全文...

习题解答继续艰难推进中，目前是0.5版本，相比0.4版，跳过了8、9章，先做了第10、11章统计力学部分的习题。

第10章有10道习题，第11章其实没有习题。看上去很少，但其实每一道习题的难度都很大。这两章的主要内容都是在用路径积分方法算统计力学中的配分函数，这本来就是一个很艰辛的课题。加上费曼在书中那形象的描述，容易让读者能够认识到大概，但是却很难算下去。事实上，这一章的习题，我参考了相当多的资料，中文的、英文的都有，才勉强完成了。

虽说是完成，但10道题目中，我只完成了9道，其中问题10-3是有困惑的，我感觉的结果跟费曼给出的不一样，因此就算不下去了。在这里提出来，希望了解的读者赐教。

点击阅读全文...

泊松分布，适合于描述单位时间内随机事件发生的次数的概率分布，如某一服务设施在一定时间内受到的服务请求的次数、汽车站台的候客人数等。^{[维基百科]}泊松分布也可以作为小概率的二项分布的近似，其推导过程在一般的概率论教材都会讲到。可是一般教材上给出的证明并不是那么让人赏心悦目，如《概率论与数理统计教程》（第二版，茆诗松等编）的第98页就给出的证明过程。那么，哪个证明过程才更让人点赞呢？我认为是利用母函数的证明。

二项分布的母函数为
$$\begin{equation}(q+px)^n,\quad q=1-p\end{equation}$$

点击阅读全文...

文件说明：

1. image.py——图像处理函数，主要是特征提取；

2. model_training.py——训练CNN单字识别模型（需要较高性能的服务器，最好有GPU加速，否则真是慢得要死）；

3. ocr.py——识别函数，包括单字分割、前面训练好的模型进行单字识别、动态规划提升效果；

4. main.py——主文件，用来调用1、3两个文件。

5、我们的模型中包含的字.txt(UTF-8编码)

点击阅读全文...

随着NLP的发展，像Word2Vec、Glove这样的词向量模型，正逐渐地被基于Transformer的BERT等模型代替，不过经典始终是经典，词向量模型依然在不少场景发光发热，并且仍有不少值得我们去研究的地方。本文我们来关心一个词向量模型可能有的疑惑：词向量的维度大概多少才够？

先说结论，笔者给出的估算结果是
\begin{equation}n > 8.33\log N\label{eq:final}\end{equation}
更简约的话可以直接记$n > 8\log N$，其中$N$是词表大小，$n$就是词向量维度，$\log$是自然对数。当$n$超过这个阈值时，就说明模型有足够的容量容纳这$N$个词语（当然$n$越大过拟合风险也越大）。这样一来，当$N=100000$时，得到的$n$大约是96，所以对于10万个词的词向量模型来说，维度选择96就足够了；如果要容纳500万个词，那么$n$大概就是128。

点击阅读全文...

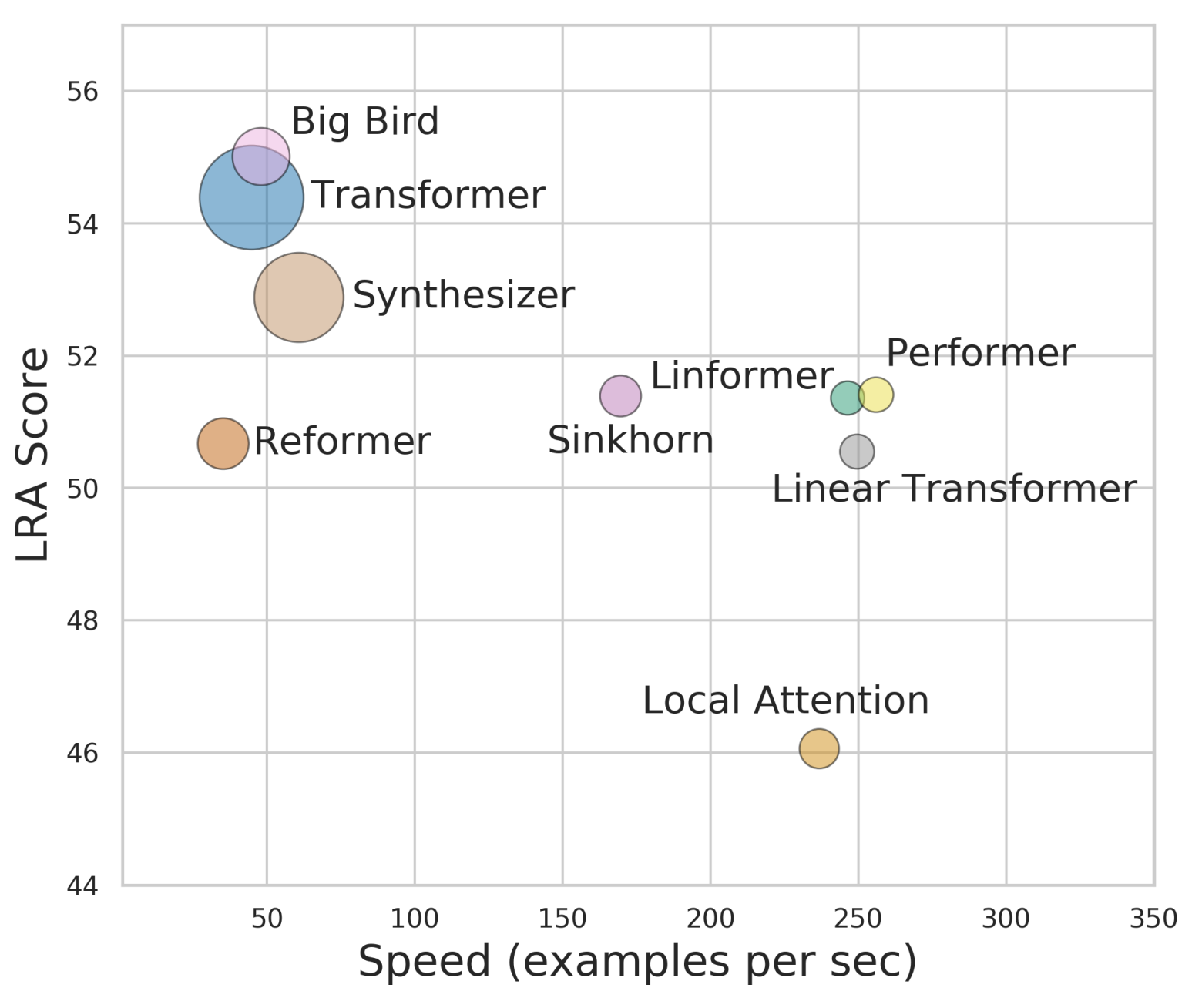
Attention机制的$\mathcal{O}(n^2)$复杂度是一个老大难问题了，改变这一复杂度的思路主要有两种：一是走稀疏化的思路，比如我们以往介绍过的Sparse Attention以及Google前几个月搞出来的Big Bird，等等；二是走线性化的思路，这部分工作我们之前总结在《线性Attention的探索：Attention必须有个Softmax吗？》中，读者可以翻看一下。本文则介绍一项新的改进工作Performer，出自Google的文章《Rethinking Attention with Performers》，它的目标相当霸气：通过随机投影，在不损失精度的情况下，将Attention的复杂度线性化。

各个Transformer模型的“效果-速度-显存”图，纵轴是效果，横轴是速度，圆圈的大小代表所需要的显存。理论上来说，越靠近右上方的模型越好，圆圈越小的模型越好

说直接点，就是理想情况下我们可以不用重新训练模型，输出结果也不会有明显变化，但是复杂度降到了$\mathcal{O}(n)$！看起来真的是“天上掉馅饼”般的改进了，真的有这么美好吗？

点击阅读全文...

也许大家会觉得，相对论中有一个因子
$$\gamma =\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$$
因此，相对论的效应只有在高速情况下，即v比较接近于c的情况下才会凸显出来。这在一般情况下是正确的，但是却不全对。因为存在相当明显的、速度低于1mm/s的相对论效应——那就是几乎人尽皆知的“磁”。

之前已经提及过，磁场可以解释为电场的相对论效应，因此所有电磁现象都可以归因为电场和相对论。事实上，这是正确的，只是教科书上并没有明确说出这一点而已。于是我们就不难理解“为什么电磁学的麦克斯韦方程组会与相对论协调”、“为什么电场与磁场的表现如此相似”等等问题了，因为它们的探究本身就在相对论的框架下，磁场和电场都是一个东西的结果。

点击阅读全文...

每当看到数学的两个看似毫不相关的分支巧妙地联系了起来时，我总会为数学的神奇美丽惊叹不已。在很久以前，当我看到通过生成函数法把数论问题与复变函数方法结合起来，衍生出一门奇妙的“解析数论”时，我就惊叹过生成函数法的漂亮！可惜，一直都没有好好写整理这些内容。今天，当我在看李政道先生的《物理学中的数学方法》时，看到他把复变函数跟随机游动如鬼斧神工般了起来，再次让我拍案叫绝。最后实在压抑不住心中的激动，在此写写概率论和生成函数的事情。

数论与复变函数结合，就生成了一门“解析数论”，按照这个说法，概率与复变函数结合，应该就会有一门“解析概率”，但是我在网上搜索的时候，并没有发现这个名词的存在。经过如此，本文还是试用了这个名词。虽然这个名词没有流行，但事实上，解析概率的方法并不算新，它可以追溯到伟大的数学家拉普拉斯以及他的著作《分析概率论》中。尽管如此，这种巧妙漂亮的方法似乎没有得到大家应该有的充分的认识。

我觉得，即使作为一个简洁的计算工具，生成函数法这个美丽的技巧，也应该尽可能为科学爱好者所知，更不用说数学专业的朋友了。

点击阅读全文...