科学空间|Scientific Spaces

开始了，成与否，期待吧！
我们能够做的，也只有期待......

简介
12月7日起，192个国家的环境部长和其他官员们将在哥本哈根召开联合国气候会议，商讨《京都议定书》一期承诺到期后的后续方案，就未来应对气候变化的全球行动签署新的协议。这是继《京都议定书》后又一具有划时代意义的全球气候协议书，毫无疑问，对地球今后的气候变化走向产生决定性的影响。这是一次被喻为“拯救人类的最后一次机会”的会议。会议将在现代化的Bella中心举行，为期两周。联合国气候会议一年召开一次，其前身为1992年在里约热内卢召开的地球峰会，地球峰会的目的是协调应对气候变化而采取的国际行动。

点击阅读全文...

在2009.12期《天文爱好者》上就公布了网址，一直到最近，网站才开通，郁闷...
报名网址：http://cnao2010.bjp.org.cn/

继在广东省天文奥赛中获得了小小的奖励之外，我一直希望参加全国天文奥赛，现在终于可以实现了。

点击阅读全文...

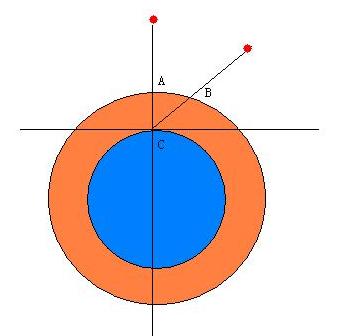
天文学中有一个名词Airmass，注意这并非Air mass（空气质量），这是指天顶距等于z的方向上大气光学厚度和天顶方向大气光学厚度之比，我目前也找不到它的中文名称究竟是什么，反正觉得如果译成“大气质量”很怪，就暂且翻译成“大气厚度指数”好了。现在知道它叫做“大气光学质量”了，一般用X表示，如下图中，$X={BC}/{AC}$。

星光传播示意图

在一片较小的区域内，大气层和地面都可以视为平行平面，这时有一个很好的近似公式：
$$X=\sec z$$
对于现在的中学教材来说，有的读者可能不了解\sec为何物，实际上：$\sec z=\frac{1}{\cos z}$

点击阅读全文...

呵呵，做了一回标题党，可能说得夸张了一点。说是“终极算法”，主要是因为它可以任意提高精度、而且几乎可以应付任何非线性方程（至少理论上是这样），提高精度是已知的迭代式上添加一些项，而不是完全改变迭代式的形式，当然在提高精度的同时，计算量也会随之增大。其理论基础依旧是泰勒级数。

我们考虑方程$x=f(y)$，已知y求x是很容易的，但是已知x求y并不容易。我们考虑把y在$(x_0,y_0)$处展开成x的的泰勒级数。关键是求出y的n阶导数$\frac{d^n y}{dx^n}$。我们记$f^{(n)}(y)=\frac{d^n x}{dy^n}$，并且有
$$\frac{dy}{dx}=\frac{1}{(\frac{dx}{dy})}=f'(y)^{-1}$$

点击阅读全文...

前几天做到了一道不等式题目，求2a-b的值域。其中
$$1 < a + b < 2\tag{1}$$ $$-2 < a - b < -1\tag{2}$$
老师很高兴地把两式左右两边加起来，得到$-1<2a<1$；然后把第二式乘以(-1)，得到$1 < b - a < 2$，然后再与(1)相加，得到$2 < 2 b< 4 \Rightarrow 1 < b < 2$；接着把这式子乘上(-1)，然后与$-1<2a<1$相加。于是结果很显然，$-3<2a-b<0$。读者们，你们觉得这做法有问题吗？

点击阅读全文...

这首歌是凤儿介绍的，去年我们学校高一夏令营的“主题歌曲”。她说歌词写得很好，我感觉也挺不错的^_^

萍，指的是漂浮在水面上的一种藻类，风吹过来，它们就会在风的作用力下聚在一起。人好象是浮在水面上的荷叶，聚散不过都是风吹动所致，到处飘散而已。因此便有了“萍水相逢”这一成语，指的是无心的邂逅或偶然的相遇。“萍聚”亦然。

曾有宋词写道“风中柳絮水中萍,聚散两无情”，这便让我们倍感人生悲欢离合的无奈。在这个充斥着高考的离别的六月里，离愁味道更浓了。可是，不论如何，明天的事情与我们无关，我们要珍惜今天事，珍惜今天人，尽我所能把握好我所拥有的。正如——

Cherish someone special for you and let them know you cherish them.

这样，当我们真的面临无可奈何的离别时，也能够含泪而微笑地挥手，唱着“只要我们曾经拥有过...”。这就是《萍聚》的声音！

点击阅读全文...

在之前的一篇向量系列的文章中，我们通过结合物理与向量来巧妙地推导出了曲线（包括平面和空间的）的曲率半径为
$$R=\frac{v^2}{a_c}=\frac{|\dot{\vec{r}}|^3}{|\dot{\vec{r}}\times \ddot{\vec{r}}|}\tag{1}$$
曲率则是曲率半径的导数：$\rho=\frac{1}{R}$。我们反过来思考一下：曲率恒定的平面曲线是否只有圆？

答案貌似是很显然的，我们需要证明一下。

由于只是考虑平面情况，我们先设$\dot{\vec{r}}=(v cos\theta,v sin\theta)=z=ve^{i\theta}$，代入(1)得到
$\frac{\dot{\theta}}{v}=\rho$————(2)

点击阅读全文...

在数学竞赛中，很多题目都专门设置了一种技巧，这种技巧在很大程度上是不怎么理所当然的，换句话说，难以“顺理成章”地想下去，或者是说方法不成系统的，这也是我有点不喜欢数学竞赛题目的一个原因。当然，另一方面，个人认为数学竞赛比物理竞赛更能锻炼一个人的思维能力，尤其是在抽象思维以及几何想象能力等，因此做一些这样的题目也会有好处的。

下面就是一道很经典的竞赛题，它是在韩国举行的第42届IMO中的题目：

设a,b,c都是正实数，求证：
$\frac{a}{\sqrt{a^2+8bc}}+ \frac{b}{\sqrt{b^2+8ac}} + \frac{c}{\sqrt{c^2+8ab}} \geq 1$

点击阅读全文...