科学空间|Scientific Spaces

测地线

黎曼度量应该是不难理解的，在微分几何的教材中，我们就已经学习过曲面的“第一基本形式”了，事实上两者是同样的东西，只不过看待问题的角度不同，微分几何是把曲面看成是三维空间中的二维子集，而黎曼几何则是从二维曲面本身内蕴地研究几何问题。

几何关心什么问题呢？事实上，几何关心的是与变换无关的“客观实体”（或者说是在变换之下不变的东西），这也是几何的定义。根据Klein提出的《埃尔朗根纲领》，几何就是研究在某种变换（群）下的不变性质的学科。如果把变换局限为刚性变换（平移、旋转、反射），那么就是欧式几何；如果变换为一般的线性变换，那就是仿射几何。而黎曼几何关心的是与一切坐标都无关的客观实体。比如说，我有一个向量，方向和大小都确定了，在直角坐标系是$(1, 1)$，在极坐标系是$(\sqrt{2}, \pi/4)$，虽然两个坐标系下的分量不同，但它们都是指代同一个向量。也就是说向量本身是客观存在的实体，跟所使用的坐标无关。从代数层面看，就是只要能够通过某种坐标变换相互得到的，我们就认为它们是同一个东西。

因此，在学习黎曼几何时，往“客观实体”方向思考，总是有益的。

平面上的测地线

有了度规，可以很自然地引入“测地线”这一实体。狭义来看，它就是两点间的最短线——是平直空间的直线段概念的推广（实际的测地线不一定是最短的，但我们先不纠结细节，而且这不妨碍我们理解它，因为测地线至少是局部最短的）。不难想到，只要两点确定了，那么不管使用什么坐标，两点间的最短线就已经确定了，因此这显然是一个客观实体。有一个简单的类比，就是不管怎么坐标变换，一个函数$f(x)$的图像极值点总是确定的——不管你变还是不变，它就在那儿，不偏不倚。

点击阅读全文...

写在前面

在《理解黎曼几何》系列，笔者分享了一些黎曼几何的“几何”心得，同时遗留了一个问题：怎么真正地去算黎曼张量？MTW的《引力论》中提到了一种基于外微分的方法，可是我不熟悉外微分，遂学习了一番。确实，是《引力论》中快捷计算曲率张量的步骤让笔者决定深入了解外微分的。果然，可观的效益是第一推动力。

这系列文章主要分享一些外微分的学习心得，曾经过多次修改和完善，包含的内容很多，比如外积、活动标架、外微分及其在黎曼几何的一些应用等，最后包括一种计算曲率的有效方式。

符号说明：在本系列中，用粗体的字母表示向量、矩阵以及基底，用普通字母来表示标量，它有可能是一个标量函数，也有可能是向量的分量，如无说明，则用$n$表示空间（流形）的维度。本文中同样使用了爱因斯坦求和法则，即相同的上下指标表示$1\sim n$遍历求和，即$\alpha_{\mu}\beta^{\mu}=\sum_{\mu=1}^{n} \alpha_{\mu}\beta^{\mu}$，习惯上将下标写在前面，比如$\alpha_{\mu}\beta^{\mu}$事实上跟$\beta^{\mu}\alpha_{\mu}$等价，但习惯写成前者。常用的一些记号是：$\mu,\nu$表示分量指标，$x^{\mu}$表示点的坐标分量，$dx^{\mu}$表示切向量（微元）的分量，$\alpha,\beta,\omega$等希腊字母也常用来表示微分形式。符号的使用有重复的地方，但符号的意义基本都在符号出现的附近有说明，因此应该不至于混淆。

最后，就是笔者其实对外微分还不是特别有感觉，因此文章中可能出现谬误之处，请读者见谅并指出。本系列命名为“外微分浅谈”，不是谦虚，确实是很浅，认识得浅，说的也很浅～

点击阅读全文...

闲聊

这两年，知识图谱、问答系统、聊天机器人等领域是越来越火了。知识图谱是一个很泛化的概念，在我看来，涉及到知识库的构建、检索、利用等机器学习相关的内容，都算知识图谱。当然，这也不是个什么定义，只是个人的直观感觉。

做知识图谱的读者都知道，三元组是结构化知识的一种方法，是做知识型问答系统的重要组成部分。对于英文领域，已经有一些较大的开源的三元组语料库，而很显然，中文目前还没有这样的语料库共享（哪怕有人爬取到了，也珍藏起来了）。笔者前段时间写了个百度百科的爬虫，爬了一段时间，抓了几百万个百度百科的词条。其中不少词条含有一些结构化的信息，直接抽取出来，就是有效的“三元组”了，可以用来做知识图谱。本文分享的三元组语料正是由此而来，共有2500万个三元组。

百度百科的三元组

点击阅读全文...

昨天刷arxiv时发现了一篇来自星星韩国的论文，名字很直白，就叫做《A Simple yet Effective Way for Improving the Performance of GANs》。打开一看，发现内容也很简练，就是提出了一种加强GAN的判别器的方法，能让GAN的生成指标有一定的提升。

作者把这个方法叫做Cascading Rejection，我不知道咋翻译，扔到百度翻译里边显示“级联抑制”，想想看好像是有这么点味道，就暂时这样叫着了。介绍这个方法倒不是因为它有多强大，而是觉得它的几何意义很有趣，而且似乎有一定的启发性。

正交分解

GAN的判别器一般是经过多层卷积后，通过flatten或pool得到一个固定长度的向量$\boldsymbol{v}$，然后再与一个权重向量$\boldsymbol{w}$做内积，得到一个标量打分（先不考虑偏置项和激活函数等末节）：
\begin{equation}D(\boldsymbol{x})=\langle \boldsymbol{v},\boldsymbol{w}\rangle\end{equation}
也就是说，用$\boldsymbol{v}$作为输入图片的表征，然后通过$\boldsymbol{v}$和$\boldsymbol{w}$的内积大小来判断出这个图片的“真”的程度。

点击阅读全文...

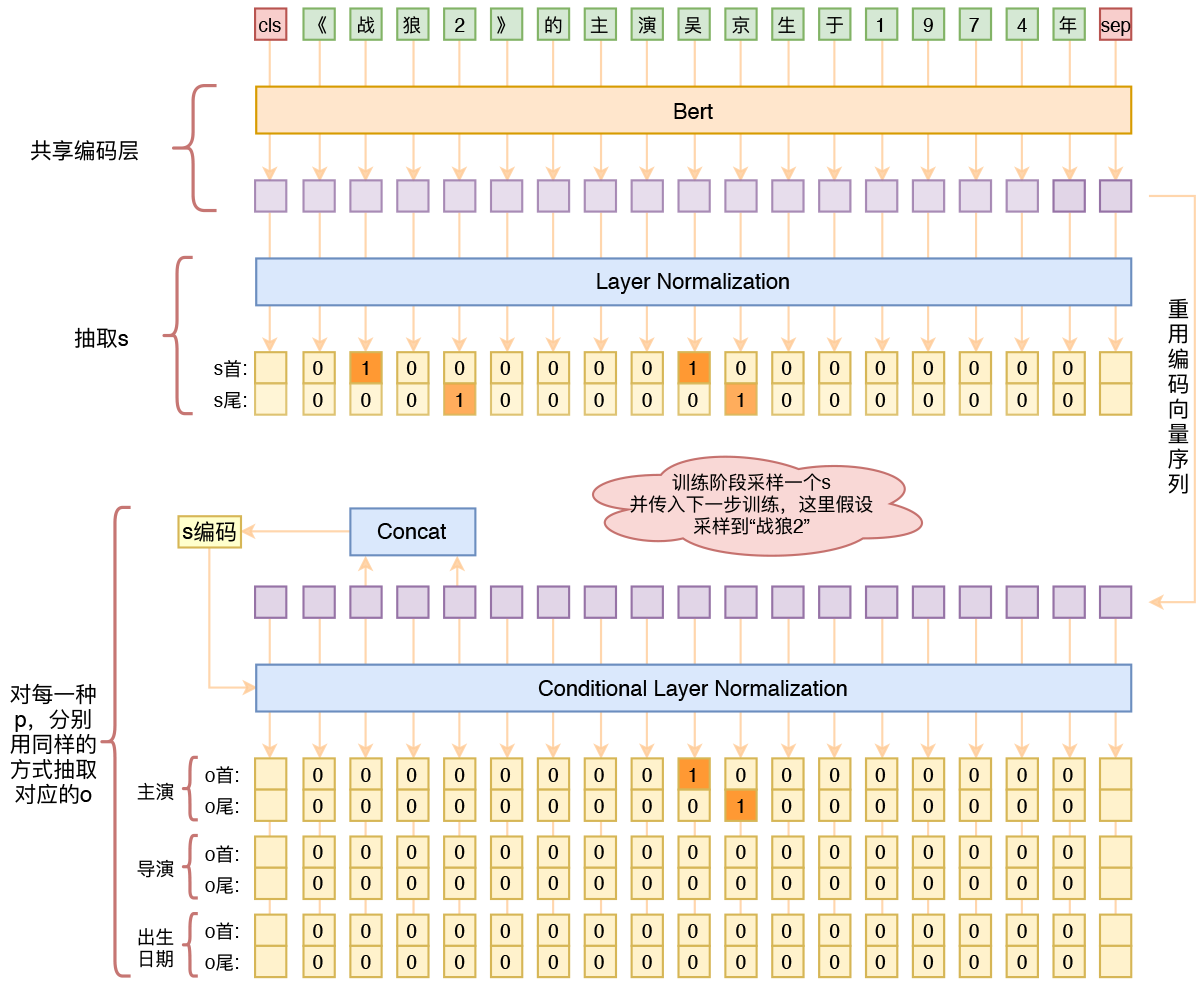
在开发bert4keras的时候就承诺过，会逐渐将之前用keras-bert实现的例子逐渐迁移到bert4keras来，而那里其中一个例子便是三元组抽取的任务。现在bert4keras的例子已经颇为丰富了，但还没有序列标注和信息抽取相关的任务，而三元组抽取正好是这样的一个任务，因此就补充上去了。

基于Bert的三元组抽取模型结构示意图

点击阅读全文...

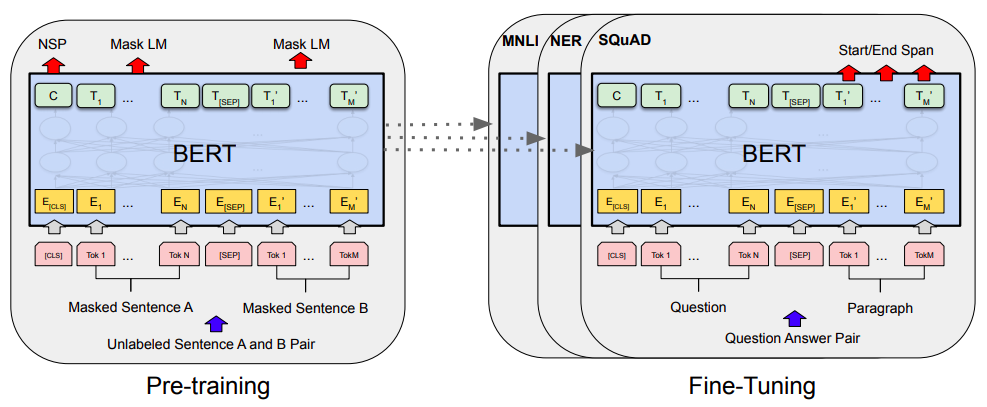
Bert是什么，估计也不用笔者来诸多介绍了。虽然笔者不是很喜欢Bert，但不得不说，Bert确实在NLP界引起了一阵轩然大波。现在不管是中文还是英文，关于Bert的科普和解读已经满天飞了，隐隐已经超过了当年Word2Vec刚出来的势头了。有意思的是，Bert是Google搞出来的，当年的word2vec也是Google搞出来的，不管你用哪个，都是在跟着Google大佬的屁股跑啊～

Bert刚出来不久，就有读者建议我写个解读，但我终究还是没有写。一来，Bert的解读已经不少了，二来其实Bert也就是基于Attention的搞出来的大规模语料预训练的模型，本身在技术上不算什么创新，而关于Google的Attention我已经写过解读了，所以就提不起劲来写了。

Bert的预训练和微调（图片来自Bert的原论文）

总的来说，我个人对Bert一直也没啥兴趣，直到上个月末在做信息抽取比赛时，才首次尝试了Bert。因为后来想到，即使不感兴趣，终究也是得学会它，毕竟用不用是一回事，会不会又是另一回事。再加上在Keras中使用（fine tune）Bert，似乎还没有什么文章介绍，所以就分享一下自己的使用经验。

点击阅读全文...

百度的“2020语言与智能技术竞赛”开赛了，今年有五个赛道，分别是机器阅读理解、推荐任务对话、语义解析、关系抽取、事件抽取。每个赛道中，主办方都给出了基于PaddlePaddle的baseline模型，这里笔者也基于bert4keras给出其中三个赛道的个人baseline，从中我们可以看到用bert4keras搭建baseline模型的方便快捷与简练。

地址：https://github.com/bojone/lic2020_baselines

思路简析

这里简单分析一下这三个赛道的任务特点以及对应的baseline设计。

点击阅读全文...

最近了解到一种称为“BERT-of-Theseus”的BERT模型压缩方法，来自论文《BERT-of-Theseus: Compressing BERT by Progressive Module Replacing》。这是一种以“可替换性”为出发点所构建的模型压缩方案，相比常规的剪枝、蒸馏等手段，它整个流程显得更为优雅、简洁。本文将对该方法做一个简要的介绍，给出一个基于bert4keras的实现，并验证它的有效性。

BERT-of-Theseus，原作配图

模型压缩

首先，我们简要介绍一下模型压缩。不过由于笔者并非专门做模型压缩的，也没有经过特别系统的调研，所以该介绍可能显得不专业，请读者理解。

点击阅读全文...