科学空间|Scientific Spaces

本文我们继续之前的变分自编码器系列，分析一下如何防止NLP中的VAE模型出现“KL散度消失（KL Vanishing）”现象。本文受到参考文献是ACL 2020的论文《A Batch Normalized Inference Network Keeps the KL Vanishing Away》的启发，并自行做了进一步的完善。

值得一提的是，本文最后得到的方案还是颇为简洁的——只需往编码输出加入BN（Batch Normalization），然后加个简单的scale——但确实很有效，因此值得正在研究相关问题的读者一试。同时，相关结论也适用于一般的VAE模型（包括CV的），如果按照笔者的看法，它甚至可以作为VAE模型的“标配”。

最后，要提醒读者这算是一篇VAE的进阶论文，所以请读者对VAE有一定了解后再来阅读本文。

VAE简单回顾

这里我们简单回顾一下VAE模型，并且讨论一下VAE在NLP中所遇到的困难。关于VAE的更详细介绍，请读者参考笔者的旧作《变分自编码器（一）：原来是这么一回事》、《变分自编码器（二）：从贝叶斯观点出发》等。

VAE的训练流程

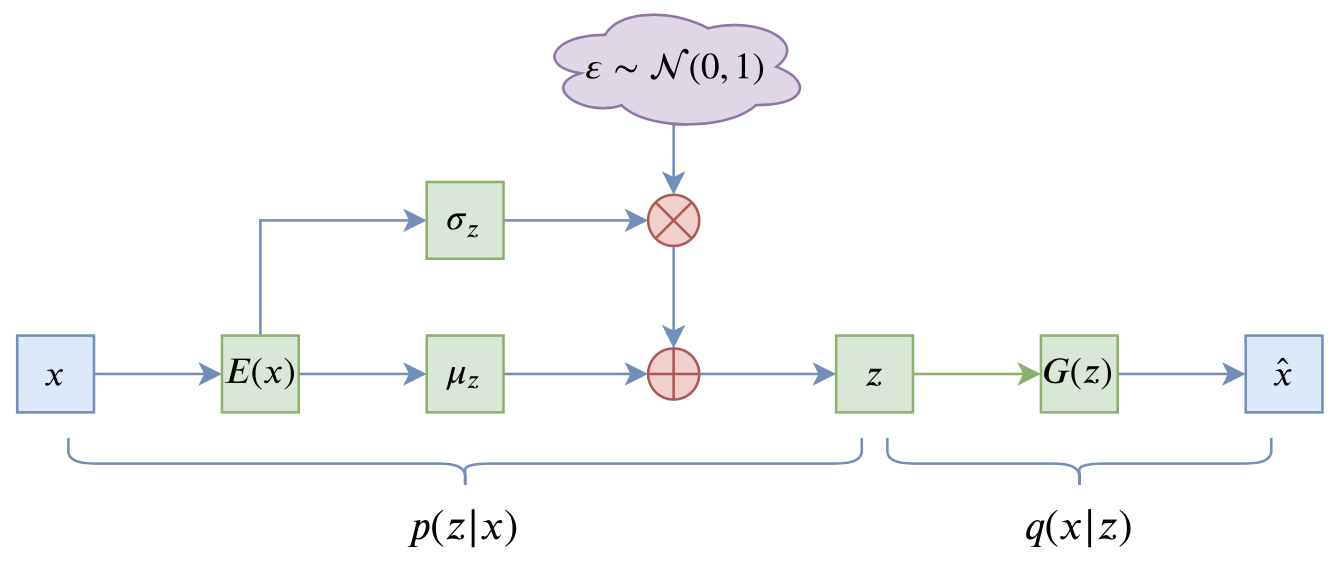
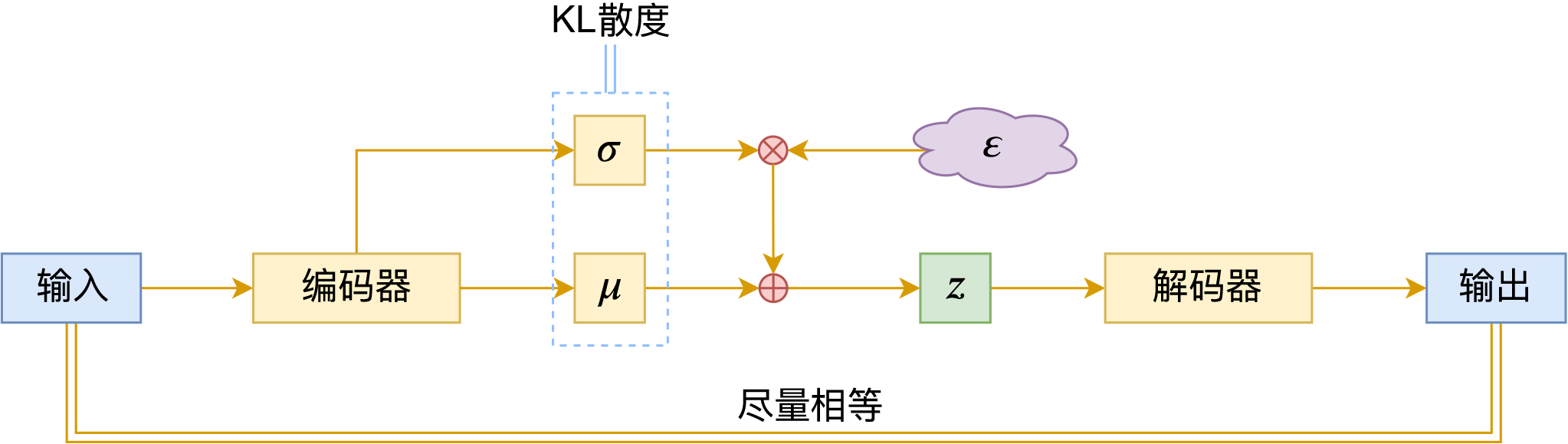
VAE的训练流程大概可以图示为

VAE训练流程图示

点击阅读全文...

由于VAE中既有编码器又有解码器（生成器），同时隐变量分布又被近似编码为标准正态分布，因此VAE既是一个生成模型，又是一个特征提取器。在图像领域中，由于VAE生成的图片偏模糊，因此大家通常更关心VAE作为图像特征提取器的作用。提取特征都是为了下一步的任务准备的，而下一步的任务可能有很多，比如分类、聚类等。本文来关心“聚类”这个任务。

一般来说，用AE或者VAE做聚类都是分步来进行的，即先训练一个普通的VAE，然后得到原始数据的隐变量，接着对隐变量做一个K-Means或GMM之类的。但是这样的思路的整体感显然不够，而且聚类方法的选择也让我们纠结。本文介绍基于VAE的一个“一步到位”的聚类思路，它同时允许我们完成无监督地完成聚类和条件生成。

理论

一般框架

回顾VAE的loss（如果没印象请参考《变分自编码器（二）：从贝叶斯观点出发》）：
$$KL\Big(p(x,z)\Big\Vert q(x,z)\Big) = \iint p(z|x)\tilde{p}(x)\ln \frac{p(z|x)\tilde{p}(x)}{q(x|z)q(z)} dzdx\tag{1}$$
通常来说，我们会假设$q(z)$是标准正态分布，$p(z|x),q(x|z)$是条件正态分布，然后代入计算，就得到了普通的VAE的loss。

点击阅读全文...

这篇文章很简短，主要描述的是一个很有用、也不复杂、但是我居然这么久才发现的事实～

在《深度学习的互信息：无监督提取特征》一文中，我们通过先验分布和最大化互信息两个loss的加权组合来得到Deep INFOMAX模型最后的loss。在那篇文章中，虽然把故事讲完了，但是某种意义上来说，那只是个拼凑的loss。而本文则要证明那个loss可以由变分自编码器自然地导出来。

过程

不厌其烦地重复一下，变分自编码器（VAE）需要优化的loss是
\begin{equation}\begin{aligned}&KL(\tilde{p}(x)p(z|x)\Vert q(z)q(x|z))\\
=&\iint \tilde{p}(x)p(z|x)\log \frac{\tilde{p}(x)p(z|x)}{q(x|z)q(z)} dzdx\end{aligned}\end{equation}
相关的论述在本博客已经出现多次了。VAE中既包含编码器，又包含解码器，如果我们只需要编码特征，那么再训练一个解码器就显得很累赘了。所以重点是怎么将解码器去掉。

其实再简单不过了，把VAE的loss分开两部分

点击阅读全文...

前段时间公司组织技术分享，轮到笔者时，大家希望我讲讲VAE。鉴于之前笔者也写过变分自编码器系列，所以对笔者来说应该也不是特别难的事情，因此就答应了下来，后来仔细一想才觉得犯难：怎么讲才好呢？

变分自编码器示意图

对于VAE来说，之前笔者有两篇比较系统的介绍：《变分自编码器（一）：原来是这么一回事》和《变分自编码器（二）：从贝叶斯观点出发》。后者是纯概率推导，对于不做理论研究的人来说其实没什么意义，也不一定能看得懂；前者虽然显浅一点，但也不妥，因为它是从生成模型的角度来讲的，并没有说清楚“为什么需要VAE”（说白了，VAE可以带来生成模型，但是VAE并不一定就为了生成模型），整体风格也不是特别友好。

笔者想了想，对于大多数不了解但是想用VAE的读者来说，他们应该只希望大概了解VAE的形式，然后想要知道“VAE有什么作用”、“VAE相比AE有什么区别”、“什么场景下需要VAE”等问题的答案，对于这种需求，上面两篇文章都无法很好地满足。于是笔者尝试构思了VAE的一种几何图景，试图从几何角度来描绘VAE的关键特性，在此也跟大家分享一下。

点击阅读全文...

在《变分自编码器（五）：VAE + BN = 更好的VAE》中，我们讲到了NLP中训练VAE时常见的KL散度消失现象，并且提到了通过BN来使得KL散度项有一个正的下界，从而保证KL散度项不会消失。事实上，早在2018年的时候，就有类似思想的工作就被提出了，它们是通过在VAE中改用新的先验分布和后验分布，来使得KL散度项有一个正的下界。

该思路出现在2018年的两篇相近的论文中，分别是《Hyperspherical Variational Auto-Encoders》和《Spherical Latent Spaces for Stable Variational Autoencoders》，它们都是用定义在超球面的von Mises–Fisher（vMF）分布来构建先后验分布。某种程度上来说，该分布比我们常用的高斯分布还更简单和有趣～

KL散度消失

我们知道，VAE的训练目标是
\begin{equation}\mathcal{L} = \mathbb{E}_{x\sim \tilde{p}(x)} \Big[\mathbb{E}_{z\sim p(z|x)}\big[-\log q(x|z)\big]+KL\big(p(z|x)\big\Vert q(z)\big)\Big]
\end{equation}

点击阅读全文...

过去虽然没有细看，但印象里一直觉得变分自编码器（Variational Auto-Encoder，VAE）是个好东西。于是趁着最近看概率图模型的三分钟热度，我决定也争取把VAE搞懂。于是乎照样翻了网上很多资料，无一例外发现都很含糊，主要的感觉是公式写了一大通，还是迷迷糊糊的，最后好不容易觉得看懂了，再去看看实现的代码，又感觉实现代码跟理论完全不是一回事啊。

终于，东拼西凑再加上我这段时间对概率模型的一些积累，并反复对比原论文《Auto-Encoding Variational Bayes》，最后我觉得我应该是想明白了。其实真正的VAE，跟很多教程说的的还真不大一样，很多教程写了一大通，都没有把模型的要点写出来～于是写了这篇东西，希望通过下面的文字，能把VAE初步讲清楚。

分布变换

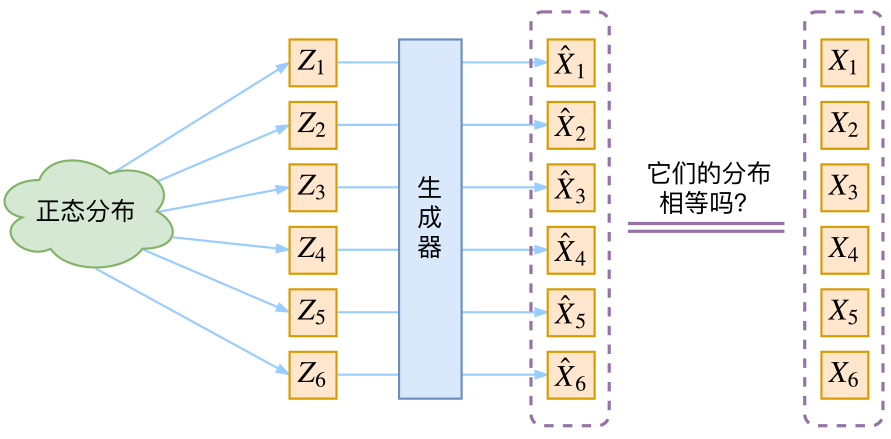
通常我们会拿VAE跟GAN比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量$Z$生成目标数据$X$的模型，但是实现上有所不同。更准确地讲，它们是假设了$Z$服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型$X=g(Z)$，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。

生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式

点击阅读全文...

源起

前几天写了博文《变分自编码器（一）：原来是这么一回事》，从一种比较通俗的观点来理解变分自编码器（VAE），在那篇文章的视角中，VAE跟普通的自编码器差别不大，无非是多加了噪声并对噪声做了约束。然而，当初我想要弄懂VAE的初衷，是想看看究竟贝叶斯学派的概率图模型究竟是如何与深度学习结合来发挥作用的，如果仅仅是得到一个通俗的理解，那显然是不够的。

所以我对VAE继续思考了几天，试图用更一般的、概率化的语言来把VAE说清楚。事实上，这种思考也能回答通俗理解中无法解答的问题，比如重构损失用MSE好还是交叉熵好、重构损失和KL损失应该怎么平衡，等等。

建议在阅读《变分自编码器（一）：原来是这么一回事》后对本文进行阅读，本文在内容上尽量不与前文重复。

准备

在进入对VAE的描述之前，我觉得有必要把一些概念性的内容讲一下。

点击阅读全文...

话说我觉得我自己最近写文章都喜欢长篇大论了，而且扎堆地来～之前连续写了三篇关于Capsule的介绍，这次轮到VAE了，本文是VAE的第三篇探索，说不准还会有第四篇～不管怎么样，数量不重要，重要的是能把问题都想清楚。尤其是对于VAE这种新奇的建模思维来说，更加值得细细地抠。

这次我们要关心的一个问题是：VAE为什么能成？

估计看VAE的读者都会经历这么几个阶段。第一个阶段是刚读了VAE的介绍，然后云里雾里的，感觉像自编码器又不像自编码器的，反复啃了几遍文字并看了源码之后才知道大概是怎么回事；第二个阶段就是在第一个阶段的基础上，再去细读VAE的原理，诸如隐变量模型、KL散度、变分推断等等，细细看下去，发现虽然折腾来折腾去，最终居然都能看明白了。

这时候读者可能就进入第三个阶段了。在这个阶段中，我们会有诸多疑问，尤其是可行性的疑问：“为什么它这样反复折腾，最终出来模型是可行的？我也有很多想法呀，为什么我的想法就不行？”

前文之要

让我们再不厌其烦地回顾一下前面关于VAE的一些原理。

VAE希望通过隐变量分解来描述数据$X$的分布
$$p(x)=\int p(x|z)p(z)dz,\quad p(x,z) = p(x|z)p(z)\tag{1}$$

点击阅读全文...