科学空间|Scientific Spaces

也许不少同好已经在一些书籍上看到过这样的论述：

各向同性的薄球壳，其内部任意一点所受到来自球壳的引力为0。

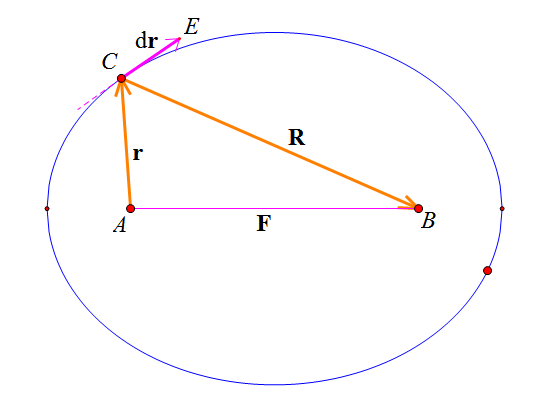
这是一个很神奇的事情，因为这意味着这是一个均匀引力场，虽然我们在很多问题上都假设了引力场均匀，但是我们却很难知道如何构造一个真正的均匀引力场（而构造一个真正的均匀力场都分析某些问题是很有用的，例如推导一些比例系数），现在眼前就摆着一个均匀引力场了。并且利用它我们就可以计算均匀实心球内部一点所受到的引力（等于它与一个球体的引力）。而关于它的证明，当然也可以利用微积分的知识，可是我们在这里介绍一个初等的方法，相信它会使我们更加感受到物理的神奇和有趣。

点击阅读全文...

美“发现”号航天飞机将于11月踏上绝唱之旅

美国航天局29日说，由于“发现”号航天飞机右侧轨道操控系统的加压部分发现两处氦气泄漏，其发射日期将被推迟一天。

“发现”号原计划美国东部时间11月1日发射升空。根据美国航天局最新安排，其发射将推迟到11月2日16时17分(北京时间3日4时17分)。这将是“发现”号计划中的绝唱之旅，也是美国航天飞机今年最后一次飞行任务。

点击阅读全文...

很多读者都知道，反射望远镜、射电望远镜、太阳能集热器等都有一个抛物状的面，它们都是利用了抛物面能将平行射入的光汇聚到一个点（焦点）上的性质。如果问为什么抛物面具有此性质，相信很多高中生都可以利用抛物线的相关知识来证明。但是，如果反过来问：为什么具有此性质的曲面是抛物面？相信会难倒一部分读者。我们来尝试寻找这一曲线（由于对称的原因，这个曲面可以看作由曲线旋转而成，因此我们可以研究曲线）。

世上最大单孔径射电望远镜

点击阅读全文...

在《为什么是抛物线？——聚光面研究》这篇文章里头，我们从光学性质出发，推导出了符合该光学性质的曲线为抛物线，同时我们也不禁感到了向量分析的美妙。也许有的读者会意犹未尽：圆锥曲线有三种，文章只介绍了一种。那好，在这篇文章里，我们就从另外两个光学性质出发，推导出符合这两个光学性质的曲线（椭圆、双曲线）。

（注：在下面的描述中，橙色加粗向量表示光线，曲线表示反射面。）

一、从一个点发出的光线经过曲线（面）反射后汇集到另外一个点上。

椭圆的光学性质

点击阅读全文...

今天上体育课的时候，BoJone与同学们正兴致勃勃地打着篮球，不料临近下课之时，同学猛一击（当然只是无意摩擦，没有恶意），我感到一阵猛疼——眼角处的肉破裂了！开始的一分钟内不停流血，奇怪的是到了校医室之后血就止住了（还没有经过任何处理，只是一直按住）。本以为只是小伤，简单处理就好，谁知校医说需要到外边的医院缝针，否则可能留疤毁容！！

既然如此严重，无奈只能服从了，简单处理伤口后就和母亲一起到了医院，缝了两针。由于接下来两天都得去医院消毒清洗伤口，所以干脆就请假回家了，周一再上学吧（貌似我在学校也仅仅是自学，没有多大区别^_^）...不过从受伤到现在，我还没有机会看到我的伤口究竟咋样...

点击阅读全文...

通过上一小节的小故事，我们已经能够基本了解最速降线的内容了，它就是要我们求出满足某一极值条件的一个未知函数，由于函数是未知的，因此这类问题被称为“泛分析”。其中还谈到，伯努利利用费马原理巧妙地得出了答案，那么我们现在就再次回顾历史，追寻伯努利的答案，并且寻找进一步的应用。

最速降线-1

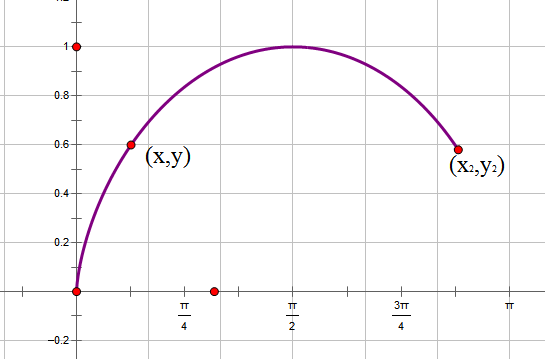
为了计算方便，我们把最速降线倒过来，把初始点设置在原点。在下落过程中，重力势能转化为动能，因此，在点(x,y)处有$\frac{1}{2} mv^2=mgy\Rightarrow v=\sqrt{2gy}$，由于纯粹为了探讨曲线形状，所以我们使g=0.5，即$v=\sqrt{y}$。在点(x,y)处所走的路程为$ds=\sqrt{dy^2+dx^2}=\sqrt{\dot{y}^2+1}dx$，所以时间为$dt=\frac{ds}{v}=\frac{\sqrt{\dot{y}^2+1}dx}{\sqrt{y}}$，于是最速降线问题就是求使$t=\int_0^{x_2} \frac{\sqrt{\dot{y}^2+1}dx}{\sqrt{y}}$最小的函数。

点击阅读全文...

2010已经成为历史了，在2011的第一天，BoJone祝大家新年快乐，生活、学习、工作都更上一层楼！我愿一直与大家探讨科学，分享科学！

一直想好好地总结一下过去的一年内的事情，无奈事情太多，一拖再拖。其实在2010年里，最值得纪念的当然就是完完整整地经历了一次天文竞赛。从3月的预选，到五月的宁夏固原决赛，接着是7月的北京集训，最后是9月下旬的北京IOAA。一步步走来的足迹，浮现在脑海，历历在目。

点击阅读全文...

2011年地球上将会发生6次“食”，其中包括四次日偏食和两次月全食。日偏食中有两次发生在遥远的南极，基本上无人可睹，其余的两次在我国的观测条件都不理想。其中1月4日那次在西北部可见，6月2日（北京时间是06.02，世界时是06.01）那次在东北部可见。

当然，上帝是公平的，我们没有比较好的日食观测，但能够观测到两次比较好的月全食。这分别发生在06.16和12.10，其中06.16那次，能够看到带食月落，而12.10那次则是全程可见。

心动了吧？让我们一同期待，那个晴朗的夜晚！

点击阅读全文...