科学空间|Scientific Spaces

在有监督的机器学习中，经常会说到训练集（train)、验证集（validation）和测试集（test），这三个集合的区分可能会让人糊涂，特别是，有些读者搞不清楚验证集和测试集有什么区别。

划分

如果我们自己已经有了一个大的标注数据集，想要完成一个有监督模型的测试，那么通常使用均匀随机抽样的方式，将数据集划分为训练集、验证集、测试集，这三个集合不能有交集，常见的比例是8:1:1，当然比例是人为的。从这个角度来看，三个集合都是同分布的。

点击阅读全文...

激活函数是神经网络中非线性的来源，因为如果去掉这些函数，那么整个网络就只剩下线性运算，线性运算的复合还是线性运算的，最终的效果只相当于单层的线性模型。

那么，常见的激活函数有哪些呢？或者说，激活函数的选择有哪些指导原则呢？是不是任意的非线性函数都可以做激活函数呢？

这里探究的激活函数是中间层的激活函数，而不是输出的激活函数。最后的输出一般会有特定的激活函数，不能随意改变，比如二分类一般用sigmoid函数激活，多分类一般用softmax激活，等等；相比之下，中间层的激活函数选择余地更大一些。

浮点误差都行！

理论上来说，只要是非线性函数，都有做激活函数的可能性，一个很有说服力的例子是，最近OpenAI成功地利用了浮点误差来做激活函数，其中的细节，请阅读OpenAI的博客：
https://blog.openai.com/nonlinear-computation-in-linear-networks/

或者阅读机器之心的介绍：
https://mp.weixin.qq.com/s/PBRzS4Ol_Zst35XKrEpxdw

点击阅读全文...

从条件概率到互信息

目前，词向量模型的原理基本都是词的上下文的分布可以揭示这个词的语义，就好比“看看你跟什么样的人交往，就知道你是什么样的人”，所以词向量模型的核心就是对上下文的关系进行建模。除了glove之外，几乎所有词向量模型都是在对条件概率$P(w|context)$进行建模，比如Word2Vec的skip gram模型就是对条件概率$P(w_2|w_1)$进行建模。但这个量其实是有些缺点的，首先它是不对称的，即$P(w_2|w_1)$不一定等于$P(w_1|w_2)$，这样我们在建模的时候，就要把上下文向量和目标向量区分开，它们不能在同一向量空间中；其次，它是有界的、归一化的量，这就意味着我们必须使用softmax等方法将它压缩归一，这造成了优化上的困难。

事实上，在NLP的世界里，有一个更加对称的量比单纯的$P(w_2|w_1)$更为重要，那就是
\[\frac{P(w_1,w_2)}{P(w_1)P(w_2)}=\frac{P(w_2|w_1)}{P(w_2)}\tag{1}\]
这个量的大概意思是“两个词真实碰面的概率是它们随机相遇的概率的多少倍”，如果它远远大于1，那么表明它们倾向于共同出现而不是随机组合的，当然如果它远远小于1，那就意味着它们俩是刻意回避对方的。这个量在NLP界是举足轻重的，我们暂且称它为“相关度“，当然，它的对数值更加出名，大名为点互信息（Pointwise Mutual Information，PMI）：
\[\text{PMI}(w_1,w_2)=\log \frac{P(w_1,w_2)}{P(w_1)P(w_2)}\tag{2}\]

有了上面的理论基础，我们认为，如果能直接对相关度进行建模，会比直接对条件概率$P(w_2|w_1)$建模更加合理，所以本文就围绕这个角度进行展开。在此之前，我们先进一步展示一下互信息本身的美妙性质。

点击阅读全文...

最后，我们来看一下词向量模型$(15)$会有什么好的性质，或者说，如此煞费苦心去构造一个新的词向量模型，会得到什么回报呢？

模长的含义

似乎所有的词向量模型中，都很少会关心词向量的模长。有趣的是，我们上述词向量模型得到的词向量，其模长还能在一定程度上代表着词的重要程度。我们可以从两个角度理解这个事实。

在一个窗口内的上下文，中心词重复出现概率其实是不大的，是一个比较随机的事件，因此可以粗略地认为
\[P(w,w) \sim P(w)\tag{24}\]
所以根据我们的模型，就有
\[e^{\langle\boldsymbol{v}_{w},\boldsymbol{v}_{w}\rangle} =\frac{P(w,w)}{P(w)P(w)}\sim \frac{1}{P(w)}\tag{25}\]
所以
\[\Vert\boldsymbol{v}_{w}\Vert^2 \sim -\log P(w)\tag{26}\]
可见，词语越高频（越有可能就是停用词、虚词等），对应的词向量模长就越小，这就表明了这种词向量的模长确实可以代表词的重要性。事实上，$-\log P(w)$这个量类似IDF，有个专门的名称叫ICF，请参考论文《TF-ICF: A New Term Weighting Scheme for Clustering Dynamic Data Streams》。

点击阅读全文...

几何词向量

上述“月老”之云虽说只是幻想，但所面临的问题却是真实的。按照传统NLP的手段，我们可以统计任意两个词的共现频率以及每个词自身的频率，然后去算它们的相关度，从而得到一个“相关度矩阵”。然而正如前面所说，这个共现矩阵太庞大了，必须压缩降维，同时还要做数据平滑，给未出现的词对的相关度赋予一个合理的估值。

在已有的机器学习方案中，我们已经有一些对庞大的矩阵降维的经验了，比如SVD和pLSA，SVD是对任意矩阵的降维，而pLSA是对转移概率矩阵$P(j|i)$的降维，两者的思想是类似的，都是将一个大矩阵$\boldsymbol{A}$分解为两个小矩阵的乘积$\boldsymbol{A}\approx\boldsymbol{B}\boldsymbol{C}$，其中$\boldsymbol{B}$的行数等于$\boldsymbol{A}$的行数，$\boldsymbol{C}$的列数等于$\boldsymbol{A}$的列数，而它们本身的大小则远小于$\boldsymbol{A}$的大小。如果对$\boldsymbol{B},\boldsymbol{C}$不做约束，那么就是SVD；如果对$\boldsymbol{B},\boldsymbol{C}$做正定归一化约束，那就是pLSA。

但是如果是相关度矩阵，那么情况不大一样，它是正定的但不是归一的，我们需要为它设计一个新的压缩方案。借鉴矩阵分解的经验，我们可以设想把所有的词都放在$n$维空间中，也就是用$n$维空间中的一个向量来表示，并假设它们的相关度就是内积的某个函数（为什么是内积？因为矩阵乘法本身就是不断地做内积）：
\[\frac{P(w_i,w_j)}{P(w_i)P(w_j)}=f\big(\langle \boldsymbol{v}_i, \boldsymbol{v}_j\rangle\big)\tag{8}\]
其中加粗的$\boldsymbol{v}_i, \boldsymbol{v}_j$表示词$w_i,w_j$对应的词向量。从几何的角度看，我们就是把词语放置到了$n$维空间中，用空间中的点来表示一个词。

因为几何给我们的感觉是直观的，而语义给我们的感觉是复杂的，因此，理想情况下我们希望能够通过几何关系来反映语义关系。下面我们就根据我们所希望的几何特性，来确定待定的函数$f$。事实上，glove词向量的那篇论文中做过类似的事情，很有启发性，但glove的推导实在是不怎么好看。请留意，这里的观点是新颖的——从我们希望的性质，来确定我们的模型，而不是反过来有了模型再推导性质。

机场-飞机+火车=火车站

点击阅读全文...

Geoffrey Hinton在谷歌多伦多办公室

由深度学习先驱Hinton开源的Capsule论文《Dynamic Routing Between Capsules》，无疑是去年深度学习界最热点的消息之一。得益于各种媒体的各种吹捧，Capsule被冠以了各种神秘的色彩，诸如“抛弃了梯度下降”、“推倒深度学习重来”等字眼层出不穷，但也有人觉得Capsule不外乎是一个新的炒作概念。

本文试图揭开让人迷惘的云雾，领悟Capsule背后的原理和魅力，品尝这一顿Capsule盛宴。同时，笔者补做了一个自己设计的实验，这个实验能比原论文的实验更有力说明Capsule的确产生效果了。

菜谱一览：

1、Capsule是什么？

2、Capsule为什么要这样做？

3、Capsule真的好吗？

4、我觉得Capsule怎样？

5、若干小菜。

点击阅读全文...

在本文中，我们再次对Capsule进行一次分析。

整体上来看，Capsule算法的细节不是很复杂，对照着它的流程把Capsule用框架实现它基本是没问题的。所以，困难的问题是理解Capsule究竟做了什么，以及为什么要这样做，尤其是Dynamic Routing那几步。

为什么我要反复对Capsule进行分析？这并非单纯的“炒冷饭”，而是为了得到对Capsule原理的理解。众所周知，Capsule给人的感觉就是“有太多人为约定的内容”，没有一种“虽然我不懂，但我相信应该就是这样”的直观感受。我希望尽可能将Capsule的来龙去脉思考清楚，使我们能觉得Capsule是一个自然、流畅的模型，甚至对它举一反三。

在《揭开迷雾，来一顿美味的Capsule盛宴》中，笔者先分析了动态路由的结果，然后指出输出是输入的某种聚类，这个“从结果到原因”的过程多多少少有些望文生义的猜测成分；这次则反过来，直接确认输出是输入的聚类，然后反推动态路由应该是怎样的，其中含糊的成分大大减少。两篇文章之间有一定的互补作用。

点击阅读全文...

事实上，在论文《Dynamic Routing Between Capsules》发布不久后，一篇新的Capsule论文《Matrix Capsules with EM Routing》就已经匿名公开了（在ICLR 2018的匿名评审中），而如今作者已经公开，他们是Geoffrey Hinton, Sara Sabour, Nicholas Frosst。不出大家意料，作者果然有Hinton。

大家都知道，像Hinton这些“鼻祖级”的人物，发表出来的结果一般都是比较“重磅”的。那么，这篇新论文有什么特色呢？

在笔者的思考过程中，文章《Understanding Matrix capsules with EM Routing 》给了我颇多启示，知乎上各位大神的相关讨论也加速了我的阅读，在此表示感谢。

论文摘要

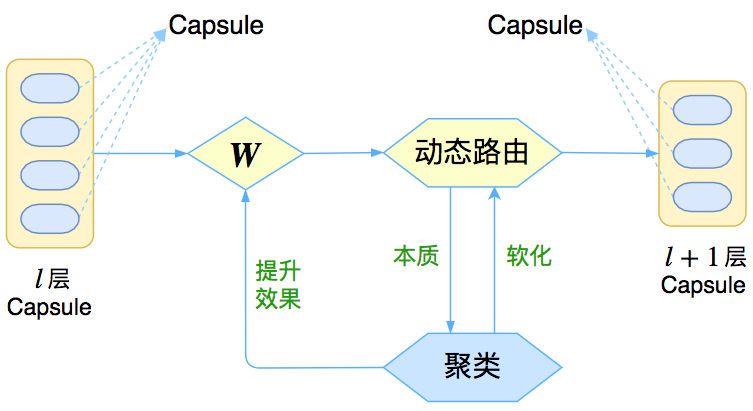
让我们先来回忆一下上一篇介绍《再来一顿贺岁宴：从K-Means到Capsule》中的那个图

Capsule框架的简明示意图

这个图表明，Capsule事实上描述了一个建模的框架，这个框架中的东西很多都是可以自定义的，最明显的是聚类算法，可以说“有多少种聚类算法就有多少种动态路由”。那么这次Hinton修改了什么呢？总的来说，这篇新论文有以下几点新东西：

1、原来用向量来表示一个Capsule，现在用矩阵来表示；

2、聚类算法换成了GMM（高斯混合模型）；

3、在实验部分，实现了Capsule版的卷积。

点击阅读全文...