21
Jul
思考：两个椭圆片能粘合成一个立体吗？
By 苏剑林 | 2019-07-21 | 58632位读者 | 引用
27
Oct
什么时候多进程的加速比可以大于1？
By 苏剑林 | 2019-10-27 | 58039位读者 | 引用多进程或者多线程等并行加速目前已经不是什么难事了，相信很多读者都体验过。一般来说，我们会有这样的结论：多进程的加速比很难达到1。换句话说，当你用10进程去并行跑一个任务时，一般只能获得不到10倍的加速，而且进程越多，这个加速比往往就越低。
要注意，我们刚才说“很难达到1”，说明我们的潜意识里就觉得加速比最多也就是1。理论上确实是的，难不成用10进程还能获得20倍的加速？这不是天上掉馅饼吗？不过我前几天确实碰到了一个加速比远大于1的例子，所以在这里跟大家分享一下。
词频统计
我的原始任务是统计词频：我有很多文章，然后我们要对这些文章进行分词，最后汇总出一个词频表出来。一般的写法是这样的：
tokens = {}
for text in read_texts():
for token in tokenize(text):
tokens[token] = tokens.get(token, 0) + 1这种写法在我统计THUCNews全部文章的词频时，大概花了20分钟。
26
Aug
HSIC简介：一个有意思的判断相关性的思路
By 苏剑林 | 2019-08-26 | 99010位读者 | 引用前几天，在机器之心看到这样的一个推送《彻底解决梯度爆炸问题，新方法不用反向传播也能训练ResNet》，当然，媒体的标题党作风我们暂且无视，主要看内容即可。机器之心的这篇文章，介绍的是论文《The HSIC Bottleneck: Deep Learning without Back-Propagation》的成果，里边提出了一种通过HSIC Bottleneck来训练神经网络的算法。
坦白说，这篇论文笔者还没有看明白，因为对笔者来说里边的新概念有点多了。不过论文中的“HSIC”这个概念引起了笔者的兴趣。经过学习，终于基本地理解了这个HSIC的含义和来龙去脉，于是就有了本文，试图给出HSIC的一个尽可能通俗（但可能不严谨）的理解。
背景
HSIC全称“Hilbert-Schmidt independence criterion”，中文可以叫做“希尔伯特-施密特独立性指标”吧，跟互信息一样，它也可以用来衡量两个变量之间的独立性。
9
Sep
重新写了之前的新词发现算法：更快更好的新词发现
By 苏剑林 | 2019-09-09 | 95436位读者 | 引用新词发现是NLP的基础任务之一，主要是希望通过无监督发掘一些语言特征（主要是统计特征），来判断一批语料中哪些字符片段可能是一个新词。本站也多次围绕“新词发现”这个话题写过文章，比如：
在这些文章之中，笔者觉得理论最漂亮的是《基于语言模型的无监督分词》，而作为新词发现算法来说综合性能比较好的应该是《更好的新词发现算法》，本文就是复现这篇文章的新词发现算法。
13
Nov
n维空间下两个随机向量的夹角分布
By 苏剑林 | 2019-11-13 | 133195位读者 | 引用昨天群里大家讨论到了$n$维向量的一些反直觉现象，其中一个话题是“一般$n$维空间下两个随机向量几乎都是垂直的”，这就跟二维/三维空间的认知有明显出入了。要从理论上认识这个结论，我们可以考虑两个随机向量的夹角$\theta$分布，并算算它的均值方差。
概率密度
首先，我们来推导$\theta$的概率密度函数。呃，其实也不用怎么推导，它是$n$维超球坐标的一个直接结论。
要求两个随机向量之间的夹角分布，很显然，由于各向同性，所以我们只需要考虑单位向量，而同样是因为各向同性，我们只需要固定其中一个向量，考虑另一个向量随机变化。不是一般性，考虑随机向量为
\begin{equation}\boldsymbol{x}=(x_1,x_2,\dots,x_n)\end{equation}
而固定向量为
\begin{equation}\boldsymbol{y}=(1,0,\dots,0)\end{equation}
31
Oct
从去噪自编码器到生成模型
By 苏剑林 | 2019-10-31 | 107603位读者 | 引用在我看来，几大顶会之中，ICLR的论文通常是最有意思的，因为它们的选题和风格基本上都比较轻松活泼、天马行空，让人有脑洞大开之感。所以，ICLR 2020的投稿论文列表出来之后，我也抽时间粗略过了一下这些论文，确实发现了不少有意思的工作。
其中，我发现了两篇利用去噪自编码器的思想做生成模型的论文，分别是《Learning Generative Models using Denoising Density Estimators》和《Annealed Denoising Score Matching: Learning Energy-Based Models in High-Dimensional Spaces》。由于常规做生成模型的思路我基本都有所了解，所以这种“别具一格”的思路就引起了我的兴趣。细读之下，发现两者的出发点是一致的，但是具体做法又有所不同，最终的落脚点又是一样的，颇有“一题多解”的美妙，遂将这两篇论文放在一起，对比分析一翻。
fashion mnist、CelebA、cifar10上的生成效果
18
Sep
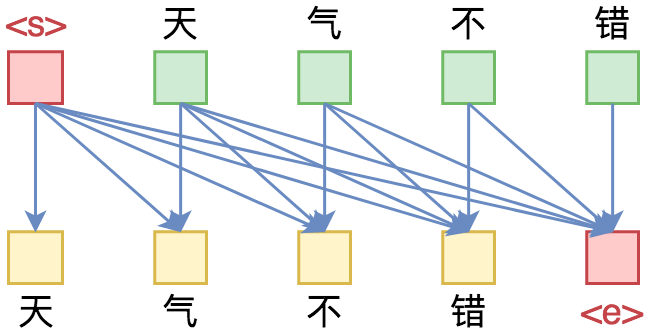
从语言模型到Seq2Seq：Transformer如戏，全靠Mask
By 苏剑林 | 2019-09-18 | 323753位读者 | 引用相信近一年来（尤其是近半年来），大家都能很频繁地看到各种Transformer相关工作（比如Bert、GPT、XLNet等等）的报导，连同各种基础评测任务的评测指标不断被刷新。同时，也有很多相关的博客、专栏等对这些模型做科普和解读。
单向语言模型图示。每预测一个token，只依赖于前面的token。
俗话说，“外行看热闹，内行看门道”，我们不仅要在“是什么”这个层面去理解这些工作，我们还需要思考“为什么”。这个“为什么”不仅仅是“为什么要这样做”，还包括“为什么可以这样做”。比如，在谈到XLNet的乱序语言模型时，我们或许已经从诸多介绍中明白了乱序语言模型的好处，那不妨更进一步思考一下：
为什么Transformer可以实现乱序语言模型？是怎么实现的？RNN可以实现吗？
本文从对Attention矩阵进行Mask的角度，来分析为什么众多Transformer模型可以玩得如此“出彩”的基本原因，正如标题所述“Transformer如戏，全靠Mask”，这是各种花式Transformer模型的重要“门道”之一。
读完本文，你或许可以了解到：
1、Attention矩阵的Mask方式与各种预训练方案的关系；
2、直接利用预训练的Bert模型来做Seq2Seq任务。
11
Oct
BN究竟起了什么作用？一个闭门造车的分析
By 苏剑林 | 2019-10-11 | 116324位读者 | 引用BN，也就是Batch Normalization，是当前深度学习模型（尤其是视觉相关模型）的一个相当重要的技巧，它能加速训练，甚至有一定的抗过拟合作用，还允许我们用更大的学习率，总的来说颇多好处（前提是你跑得起较大的batch size）。
那BN究竟是怎么起作用呢？早期的解释主要是基于概率分布的，大概意思是将每一层的输入分布都归一化到$\mathcal{N}(0,1)$上，减少了所谓的Internal Covariate Shift，从而稳定乃至加速了训练。这种解释看上去没什么毛病，但细思之下其实有问题的：不管哪一层的输入都不可能严格满足正态分布，从而单纯地将均值方差标准化无法实现标准分布$\mathcal{N}(0,1)$；其次，就算能做到$\mathcal{N}(0,1)$，这种诠释也无法进一步解释其他归一化手段（如Instance Normalization、Layer Normalization）起作用的原因。
在去年的论文《How Does Batch Normalization Help Optimization?》里边，作者明确地提出了上述质疑，否定了原来的一些观点，并提出了自己关于BN的新理解：他们认为BN主要作用是使得整个损失函数的landscape更为平滑，从而使得我们可以更平稳地进行训练。
本博文主要也是分享这篇论文的结论，但论述方法是笔者“闭门造车”地构思的。窃认为原论文的论述过于晦涩了，尤其是数学部分太不好理解，所以本文试图尽可能直观地表达同样观点。
（注：阅读本文之前，请确保你已经清楚知道BN是什么，本文不再重复介绍BN的概念和流程。）
最近评论