科学空间|Scientific Spaces

内积与外积

向量（这里暂时指的是二维或者三维空间中的向量）的强大之处，在于它定义了内积和外积（更多时候称为叉积、向量积等），它们都是两个向量之间的运算，其中，内积被定义为是对称的，而外积则被定义为反对称的，它们都满足分配律。

沿着书本的传统，我们用$\langle,\rangle$表示内积，用$\land$表示外积，对于外积，更多的时候是用$\times$，但为了不至于出现太多的符号，我们统一使用$\land$。我们将向量用基的形式写出来，比如
$$\boldsymbol{A}=\boldsymbol{e}_{\mu}A^{\mu} \tag{1} $$
其中$\boldsymbol{e}_{\mu}$代表着一组基，而$A^{\mu}$则是向量的分量。我们来计算两个向量$\boldsymbol{A},\boldsymbol{B}$的内积和外积，即
$$\begin{aligned}&\langle \boldsymbol{A}, \boldsymbol{B}\rangle=\langle \boldsymbol{e}_{\mu}A^{\mu}, \boldsymbol{e}_{\nu}B^{\nu}\rangle=\langle\boldsymbol{e}_{\mu},\boldsymbol{e}_{\nu}\rangle A^{\mu}A^{\nu}\\
&\boldsymbol{A}\land \boldsymbol{B}=(\boldsymbol{e}_{\mu}A^{\mu})\land (\boldsymbol{e}_{\nu}B^{\nu})=\boldsymbol{e}_{\mu}\land\boldsymbol{e}_{\nu} A^{\mu}B^{\nu}
\end{aligned} \tag{2} $$

点击阅读全文...

对于前面所述的外微分，包括后面还略微涉及到的微分形式的积分，都是纯粹代数定义的内容，本身不具有任何的几何意义。但是，我们可以将某些公式或者定义，与一些几何内容对应起来，使我们更深刻地理解它，并且更灵活运用它。但是，它仅仅是一种对应，而且取决于我们的诠释。比如，我们说外微分公式
$$\int_{\partial D} Pdx+Qdy = \int_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dx\land dy \tag{32} $$
对应于格林公式
$$\int_{\partial D} Pdx+Qdy = \int_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dxdy \tag{33} $$
。这是没问题的，但它们并不等价，它们仅仅是形式上刚好一样。因为格林公式是描述闭合曲线的积分跟面积分的联系，而外微分的公式是一种纯粹的代数运算。因为你完全可以将$dx\land dy$对应于$-dxdy$而不是$dxdy$，这样就得到另外一种几何的对应。

更深刻的问题是：为什么恰好有这个对应？也就是说，为什么经过一些调整和诠释后，就能够得到与积分公式的对应？首先要明确的是外积与普通的数的乘积，除了反对称性之外，是没有任何区别的，因此不少性质得以保留；其次，还应该要回到反对称本身来考虑，矩阵的行列式代表着矩阵所对应的向量组张成的$n$维立体的体积，然而行列式是反对称的，这就意味着反对称运算跟体积、积分等有着先天的联系。当然，更细致的认识，笔者也还没做到。

此外，我们说寻求微分形式的几何意义，通常只是针对不超过3维的空间来讨论的，更高维的几何图像我们很难想象出来，尤其是高维的曲面积分，一般只是类比，但类比是否成立，有时还需要进一步商榷。因此，这种情况下，倒不如干脆点，说微分形式描述的东西就是几何，而不再去寻找所谓的几何意义了。也就是说，反过来，将微分形式和外微分作为公理式的第一性原理来定义几何。

甚至，你可以只将外微分当作是一种记忆各种微分、积分公式的有效途径，比如现在我要大家默写三维空间中的斯托克斯公式，大家估计会乱，因为不一定记得是哪个减哪个。但是在外微分框架下，可以很快地将它推导一遍。好比式$(11)$，如果非要寻求几何解释，那就是开普勒第二定律：单位时间内扫过的面积相等；然而没有几何解释，你依旧可以把方程解下去。

点击阅读全文...

众所周知，要掌握黎曼几何，需要强烈的几何直观感。但除此之外，用分量语言描述的黎曼几何，也需要很好的分析能力才能梳理清楚，因为有$N$多的指标在表示着分量和求和，咋看上去处处皆指标。这种繁琐的分量语言并不总讨人喜欢，甚至在不少地方是声名狼籍的。

在分量的语言中，我们本质上可以在局部建立任意形式的坐标系，也就是采用任意形式的基底$\{\boldsymbol{e}_{\mu}\}$，或者说自然标架。但不可否认，在正交标架（标准正交基）之下，很多方程会简单不少，并且得益于我们对欧氏空间的熟练，我们对正交标架下的研究可能会更有感觉。因此，如果条件允许的话，我们应当使用正交标架$\{\hat{\boldsymbol{e}}_{\mu}\}$，哪怕是活动的，这里我们用$\hat{}$标记正交标架。

比如，我们有微元
$$d\boldsymbol{r} = \boldsymbol{e}_{\mu}dx^{\mu} \tag{12} $$
是在一般标架下测量的，那么就可以得到黎曼度量

点击阅读全文...

这里我们将展示上面一节的方法对于计算黎曼曲率张量的计算是多少的有力！我们再次列出我们得到的所有公式。首先是概念式的
$$\begin{aligned}&\omega^{\mu}=h_{\alpha}^{\mu}dx^{\alpha}\\
&d\boldsymbol{r}=\hat{\boldsymbol{e}}_{\mu} \omega^{\mu}\\
&ds^2 = \eta_{\mu\nu} \omega^{\mu}\omega^{\nu}\\
&\langle \hat{\boldsymbol{e}}_{\mu}, \hat{\boldsymbol{e}}_{\nu}\rangle = \eta_{\mu\nu}\end{aligned} \tag{65} $$
然后是
$$\begin{aligned}&d\eta_{\mu\nu}=\omega_{\nu\mu}+\omega_{\mu\nu}=\eta_{\nu\alpha}\omega_{\mu}^{\alpha}+\eta_{\mu \alpha}\omega_{\nu}^{\alpha}\\
&d\omega^{\mu}+\omega_{\nu}^{\mu}\land \omega^{\nu}=0\end{aligned} \tag{66} $$
这两个可以帮助我们确定$\omega_{\nu}^{\mu}$；接着就是
$$\mathscr{R}_{\nu}^{\mu} = d\omega_{\nu}^{\mu}+\omega_{\alpha}^{\mu} \land \omega_{\nu}^{\alpha} \tag{67} $$
最后你要正交标架下的$\hat{R}^{\mu}_{\nu\beta\gamma}$，就要写出：
$$\mathscr{R}_{\nu}^{\mu}=\sum_{\beta < \gamma} \hat{R}^{\mu}_{\nu\beta\gamma}\omega^{\beta}\land \omega^{\gamma} \tag{68} $$
如果你要原始标架下的$R^{\mu}_{\nu\beta\gamma}$，就要写出
$$(h^{-1})_{\mu'}^{\mu}\mathscr{R}^{\mu'}_{\nu'}h_{\nu}^{\nu'} = \sum_{\beta < \gamma} R^{\mu}_{\nu\beta\gamma}dx^{\beta}\land dx^{\gamma} \tag{69} $$
然后依次读出$R^{\mu}_{\nu\beta\gamma}$，就像制表一样。

点击阅读全文...

咋看上去，SVD分解是比较传统的数据挖掘手段，自编码器是深度学习中一个比较“先进”的概念，应该没啥交集才对。而本文则要说，如果不考虑激活函数，那么两者将是等价的。进一步的思考就可以发现，不管是SVD还是自编码器，我们降维，并不是纯粹地为了减少储存量或者减少计算量，而是“智能”的初步体现。

等价性

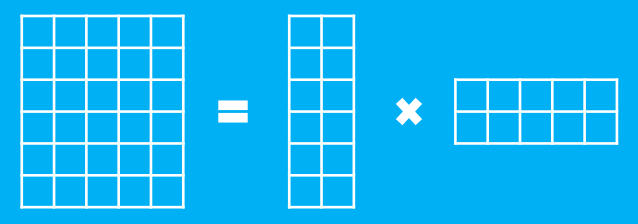
假设有一个$m$行$n$列的庞大矩阵$M_{m\times n}$，这可能使得计算甚至存储上都成问题，于是考虑一个分解，希望找到矩阵$A_{m\times k}$和$B_{k\times n}$，使得
$$M_{m\times n}=A_{m\times k}\times B_{k\times n}$$
这里的乘法是矩阵乘法。如图

SVD

点击阅读全文...

提前祝各位读者新年快乐，2017行好运～

这篇文章主要想回答两个“为什么”的问题：1、为啥我就对SVD感兴趣了？；2、为啥我说SVD是一个聚类过程？回答的内容纯粹个人思辨结果，暂无参考文献。

为什么要研究SVD？

从2015年接触深度学习到现在，已经研究了快两年的深度学习了，现在深度学习、数据科学等概念也遍地开花。为什么在深度学习火起来的时候，我反而要回去研究“古老”的SVD分解呢？我觉得，SVD作为一个矩阵分解算法，它的价值不仅仅体现在它广泛的应用，它背后还有更加深刻的内涵，即它的可解释性。在深度学习流行的今天，不少人还是觉得深度学习（神经网络）就是一个有效的“黑箱”模型。但是，仅用“黑箱”二字来解释深度学习的有效性显然不能让人满意。前面已经说过，SVD分解本质上与不带激活函数的三层自编码机等价，理解SVD分解，能够为神经网络模型寻求一个合理的概率解释。

点击阅读全文...

过程

在Python中，如果要多进程运算，一般是通过multiprocessing来实现的，常用的是multiprocessing中的进程池，比如：

from multiprocessing import Pool
import time

def f(x):
    time.sleep(1)
    print x+1
    return x+1

a = range(10)
pool = Pool(4)
b = pool.map(f, a)
pool.close()
pool.join()

print b

这样写简明清晰，确实方便，有趣的是，只需要将multiprocessing换成multiprocessing.dummy，就可以将程序从多进程改为多线程了。

点击阅读全文...

本文主要是给出了关键词的一种新的定义，并且基于Word2Vec给出了一个实现方案。这种关键词的定义是自然的、合理的，Word2Vec只是一个简化版的实现方案，可以基于同样的定义，换用其他的模型来实现。

说到提取关键词，一般会想到TF-IDF和TextRank，大家是否想过，Word2Vec还可以用来提取关键词？而且，用Word2Vec提取关键词，已经初步含有了语义上的理解，而不仅仅是简单的统计了，而且还是无监督的！

什么是关键词？

诚然，TF-IDF和TextRank是两种提取关键词的很经典的算法，它们都有一定的合理性，但问题是，如果从来没看过这两个算法的读者，会感觉简直是异想天开的结果，估计很难能够从零把它们构造出来。也就是说，这两种算法虽然看上去简单，但并不容易想到。试想一下，没有学过信息相关理论的同学，估计怎么也难以理解为什么IDF要取一个对数？为什么不是其他函数？又有多少读者会破天荒地想到，用PageRank的思路，去判断一个词的重要性？

说到底，问题就在于：提取关键词和文本摘要，看上去都是一个很自然的任务，有谁真正思考过，关键词的定义是什么？这里不是要你去查汉语词典，获得一大堆文字的定义，而是问你数学上的定义。关键词在数学上的合理定义应该是什么？或者说，我们获取关键词的目的是什么？

点击阅读全文...