《新理解矩阵4》:相似矩阵的那些事儿
By 苏剑林 | 2012-11-11 | 56005位读者 | 引用这篇文章估计是这个系列最后一篇了,也许以后会继续谈到线性代数,但是将会独立开来讲述。本文主要讲的是相似矩阵的一些事情,本文的观点很是粗糙,自己感觉都有点模糊,因此请读者细细阅读。在孟岩的文章里头,它对矩阵及其相似有了一个非常精彩的描述:
“矩阵是线性空间中的线性变换的一个描述。在一个线性空间中,只要我们选定一组基,那么对于任何一个线性变换,都能够用一个确定的矩阵来加以描述。”
同样的,对于一个线性变换,只要你选定一组基,那么就可以找到一个矩阵来描述这个线性变换。换一组基,就得到一个不同的矩阵。所有这些矩阵都是这同一个线性变换的描述,但又都不是线性变换本身。
《科学》:我们发现了磁单极子
By 苏剑林 | 2009-10-02 | 27017位读者 | 引用电与磁具有很多相似性,那么,自然界允许只带有单一电荷的电子存在,那允不允许只有一个磁极的物体存在呢?也许会有的,英国物理学家保罗·狄拉克(Paul Dirac)早在1931年利用数学公式预言了这种物质的存在,并且把它叫做“磁单极子”。而今天,我们已经发现了它们的足迹! 磁单极子是理论物理学弦理论中指一些仅带有北极或南极单一磁极的磁性物质,它们的磁感线分布类似于点电荷的电场线分布。这种物质的存在性在科学界時有纷争,截至2008年尚未发现这种物体。可以说是21世纪物理学界重要的研究主题之一。在2009年9月3日的《科学》杂志上刊载了一篇记录人类首次观测到磁单极子的论文。
《积分公式大全》电子书
By 苏剑林 | 2010-01-23 | 72177位读者 | 引用注:2019.02.13 由科学空间苏剑林(https://kexue.fm)更新,修正公式76,并简化latex。
物理、天文研究得深入了,微积分的应用自然也就多了(其实很多内容都用到微积分)。所以弄出一个几何或者力学问题,随手就列出一道积分或者微分方程,这时求解是最重要的。对于我来说,求导数可以娓娓道来,轻松而得;而积分则比较困难(这与个人的技巧有关,更重要的是事实:导数几乎有通用的公式,而积分只能“凑”出来)。
因此,很多积分干脆依靠现成的公式,懒得去推导了。然后,并非随时随地都有《数学分析》在手的,对计算机数学软件的实用又不大熟悉,这时候只能够求助这一本《积分表》了。只要不是故意去钻那些竞赛级别的数学难题,这已经足够应付物理等方面的应用了。
这时候就这也不用愁到处找$\int \sqrt{a^2-x^2}dx$的结果了。
[春礼]《方程与宇宙》:圆形限制性三体问题(七)
By 苏剑林 | 2011-02-04 | 24266位读者 | 引用平面圆形限制性三体问题运动方程及能量积分
plane circular restricted three-body problem
02.04有重要修正!!
寒假一个很大的目标就是能够在三体问题的周期轨道上有点突破,于是就出动了“向量”、“复分析”、“微分方程”等理论“核武”,遗憾的是,“有心栽花花不开”,到今天还是没有多少进展。不过俗语也说“无心插柳柳成荫”,也不错。今天回看《天体力学引论》中的“圆形限制性三体问题”,经过一番思考,利用这些天的思考方法重新推导出了其运动方程和能量积分,也算是“意外收获”在此作为春节礼物与大家分享。
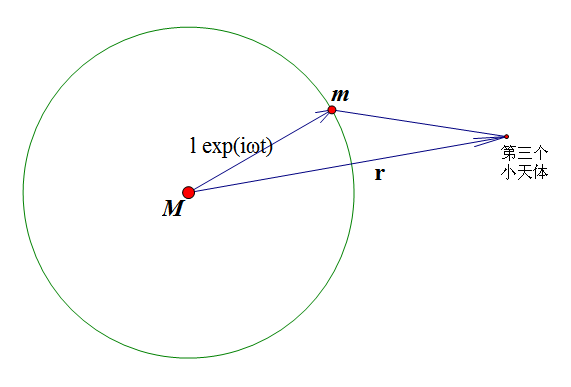
所谓“圆形限制性三体问题”,就是指两个大质量天体(质点)在它们相互引力作用下做圆周运动,假设第三天体(质量趋于0)只受到这两个天体的引力作用而不影响两个天体运行的一种运动情况。由于普通三体问题无法积分,而这个“限制性模型”能够把问题化简不少(不过还是不能积分出来的),因此也得到了一定应用。它的应用条件是:第三体质量小(如当前航天器与地球、太阳)、短程。注意短程也是相当重要的条件之一,注意短程也是相当重要的条件之一,质量越小应用范围越大。要是质量大的话,就不能计算太长的路程。
《环球科学》:超越费曼图
By 苏剑林 | 2012-11-26 | 19828位读者 | 引用虽然文章的大部分内容我都还无法弄懂,但是这里边讲述的振奋人心的内容让我决定把它转载过来。文章说,将大自然的各种力统一起来,或许没有物理学家原来所想的那么困难。
撰文∕ 伯尔尼(Zvi Bern)、狄克森(Lance J. Dixon)寇索尔(David A. Kosower)
翻译∕ 高涌泉(台湾大学物理系教授)
提供/ 科学人(Scientific American繁体中文版)
重点提要
物理学家对于粒子碰撞的了解,最近经历了一场宁静革命。知名物理学家费曼所引入的观念对于很多应用而言已到达极限。作者与合作者已经发展出新的方法。
物理学家利用新方法,可以更可靠地描述在大强子对撞机(LHC)那种极端条件下普通粒子的行为,这将帮助实验学家寻找新粒子与新作用力。
新方法还有更为深刻的应用:它让一种于1980年代被物理学家放弃的统一理论有了新生命,重力看起来像是双份的强核力一起作用。
春天某个晴朗的日子,本文作者狄克森从英国伦敦地铁的茂恩都站进入地铁,想前往希斯洛机场。伦敦地铁每天有300万名乘客,他瞧着其中一位陌生人,无聊地想着:这位老兄会从温布尔登站离开地铁的机率有多大?由于此人可能搭上任何一条地铁路线,所以该如何推算这个机率呢?他想了一会,领悟到这个问题其实跟粒子物理学家所面对的麻烦很像,那就是该如何预测现代高能实验中粒子碰撞的后果。
欧洲核子研究组织(CERN)的大强子对撞机(LHC)是这个时代最重要的探索实验;它让质子以近乎光速前进并相撞,然后研究碰撞后的碎片。我们知道建造对撞机及侦测器得用上最尖端的技术,然而较不为人知的是,解释侦测器的发现同样也是极为困难的挑战。乍看之下,它不应该那么困难才对,因为基本粒子的标准模型早已确立,理论学家也一直用此模型来预测实验的结果,而且理论预测所依赖的是著名物理学家费曼(Richard P. Feynman)早在60多年前就发展出来的计算技巧,每位粒子物理学家在研究生阶段都学过费曼的技巧;关于粒子物理的每本科普书、每篇科普文章,也都借用了费曼的概念。
《新理解矩阵1》:矩阵是什么?
By 苏剑林 | 2012-10-29 | 76820位读者 | 引用前边我承诺过会写一些关于自己对矩阵的理解。其实孟岩在《理解矩阵》这三篇文章中,已经用一种很直观的方法告诉了我们有关矩阵以及线性代数的一些性质和思想。而我对矩阵的理解,大多数也是来源于他的文章。当然,为了更好地理解线性代数,我还阅读了很多相关书籍,以求得到一种符合直觉的理解方式。孟岩的blog已经很久没有更新了,在此谨引用他的标题,来叙述我对矩阵的理解。
当然,我不打算追求那些空间、算子那些高抽象性的问题,我只是想发表一下自己对线性代数中一些常用工具的看法,比如说矩阵、行列式等。同时,文章命名为“理解矩阵”,也就是说这不是矩阵入门教程,而是与已经有一定的线性代数基础的读者一起探讨关于矩阵的其他理解方式,仅此而已。我估计基本上学过线性代数的读者都能够读懂这篇文章。
首先,我们不禁要追溯一个本源问题:矩阵是什么?
《新理解矩阵3》:行列式的点滴
By 苏剑林 | 2012-11-04 | 41684位读者 | 引用本文的最新版本位于:http://kexue.fm/archives/2208/
亲爱的读者朋友们,科学空间版的理解矩阵已经来到了BoJone认为是最激动人心的部分了,那就是关于行列式的叙述。这部分内容没有在孟岩的文章中被谈及到,是我自己结合了一些书籍和网络资源而得出的一些看法。其中最主要的书籍是《数学桥》,而追本溯源,促进我研究这方面的内容的是matrix67的那篇《教材应该怎么写》。本文包含了相当多的直观理解内容,在我看来,这部分内容也许不是正统的观点,但是至少在某种程度上能够促进我们对线性代数的理解。
大多数线性代数引入行列式的方式都是通过讲解线性方程组的,这种方式能够让学生很快地掌握它的计算,以及给出了一个最实际的应用(就是解方程组啦)。但是这很容易让读者走进一个误区,让他们认为线性代数就是研究解方程组的。这样并不能让读者真正理解到它的本质,而只有当我们对它有了一个直观熟练的感觉,我们才能很好地运用它。
行列式的出现其实是为了判断一个矩阵是否可逆的,它通过某些方式构造出一个“相对简单”的函数来达到这个目的,这个函数就是矩阵的行列式。让我们来反思一下,矩阵可逆意味着什么呢?之前已经提到过,矩阵是从一个点到另外一个点的变换,那么逆矩阵很显然就是为了把它变换回来。我们还说过,“运动是相对的”,点的变换又可以用坐标系的变换来实现。但是,按照我们的直觉,不同的坐标系除了有那些运算上的复杂度不同(比如一般的仿射坐标系计算点积比直角坐标系复杂)之外,不应该有其他的不同了,用物理的语言说,就是一切坐标系都是平权的。那么给出一个坐标系,可以自然地变换到另外一个坐标系,也可以自然地将它变换回来。既然矩阵是这种坐标系的一个描述,那么矩阵不可逆的唯一可能性就是:
这个$n$阶矩阵的$n$个列向量根本就构不成一个$n$维空间的坐标系。
《虚拟的实在(3)》——相对论动力学
By 苏剑林 | 2013-06-20 | 27730位读者 | 引用半个多月没有写文章了,一是因为接近期末考了,比较忙,当然最主要的原因还是人变懒了,呵呵,别人是忙里偷闲,我是闲里偷懒了。
这篇文章主要跟大家分享一下相对论动力学的知识。我们之前已经接触过相对论的坐标变换了,接下来的任务应该是把经典力学的动力学定律改成为相对论版本的,这显然也是学习场论的必经之路——懂得如何构造力学定律的相对版版本,是懂得构造相对论性场的基础。和朗道的《力学》与《场论》一样,我们的主线就是“最小作用量原理”。让我们回忆一下,在经典力学中,一个自由粒子的作用量是
$$S_m=\int Ldt=\int \frac{1}{2} m v^2dt$$








最近评论