施密特系统的校正镜方程求解
By 苏剑林 | 2011-02-11 | 40901位读者 | 引用非抛物面望远镜的校正镜方程求解
The Corrector Plate of Non-parabola Telescope
本文在牧夫天文论坛的讨论:
http://www.astronomy.ac/bbs/thread-160257-1-1.html
为了克服折射望远镜的色差问题,1670年,牛顿制造了第一台实用的反射式望远镜,将望远镜的主镜由玻璃透镜换成了抛物反射面,从而消除了色差。然而,相比球面镜,大口径的抛物面并不容易磨制。因为制作大球面镜只需要将曲率相等的小镜片相对自由组合在一起就行了,而抛物线每点的曲率并不相等,所以需要逐个磨制曲率不等的小镜片,并按照严格的顺序组合起来。这无疑大大增加了磨制难度。
为了解决这一难题,天文学家们想到了一个折衷的办法:以球面为主镜,并配以校正镜来校正球差。迎着这一思路,施密特望远镜随之而生。而当代的大望远镜基本上都是沿用这一思路。然而,校正镜是一个比抛物面更加复杂的四次曲面,磨制工艺要求更高,因此,校正镜也不宜过大。
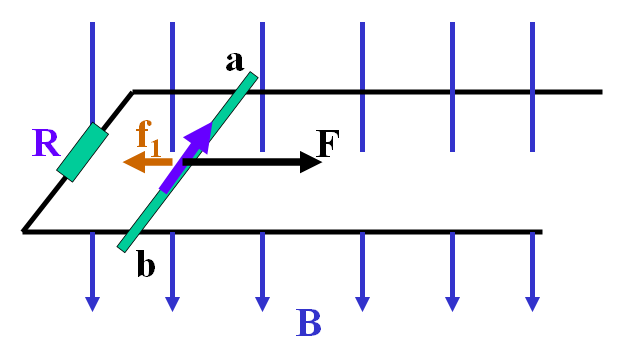
不可能事件——一道经典电磁感应题的错误
By 苏剑林 | 2011-01-09 | 52029位读者 | 引用意犹未尽——继续光学曲线
By 苏剑林 | 2010-11-13 | 72088位读者 | 引用为什么是抛物线?——聚光面研究
By 苏剑林 | 2010-11-07 | 109628位读者 | 引用当酸溶液遇到了更多的水时...
By 苏剑林 | 2010-10-31 | 31056位读者 | 引用也许不少同好已经在一些书籍上看到过这样的论述:
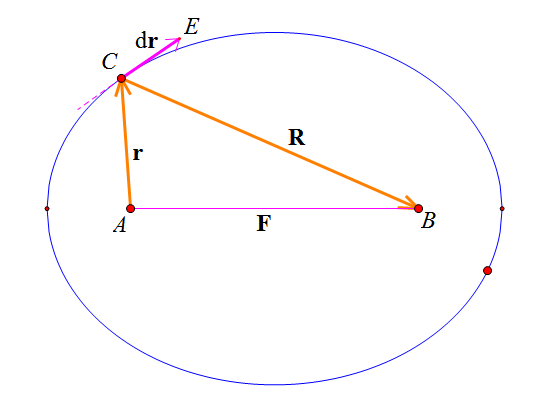
各向同性的薄球壳,其内部任意一点所受到来自球壳的引力为0。
这是一个很神奇的事情,因为这意味着这是一个均匀引力场,虽然我们在很多问题上都假设了引力场均匀,但是我们却很难知道如何构造一个真正的均匀引力场(而构造一个真正的均匀力场都分析某些问题是很有用的,例如推导一些比例系数),现在眼前就摆着一个均匀引力场了。并且利用它我们就可以计算均匀实心球内部一点所受到的引力(等于它与一个球体的引力)。而关于它的证明,当然也可以利用微积分的知识,可是我们在这里介绍一个初等的方法,相信它会使我们更加感受到物理的神奇和有趣。












最近评论