通过互信息思想来缓解类别不平衡问题

类别不平衡问题，也叫“长尾问题”，是机器学习面临的常见问题之一，尤其是来源于真实场景下的数据集，几乎都是类别不平衡的。大概在两年前，笔者也思考过这个问题，当时正好对“互信息”相关的内容颇有心得，所以构思了一种基于互信息思想的解决办法，但又想了一下，那思路似乎过于平凡，所以就没有深究。然而，前几天在arxiv上刷到Google的一篇文章《Long-tail learning via logit adjustment》，意外地发现里边包含了跟笔者当初的构思几乎一样的方法，这才意识到当初放弃的思路原来还能达到SOTA的水平～于是结合这篇论文，将笔者当初的构思过程整理于此，希望不会被读者嫌弃“马后炮”。

问题描述 #

这里主要关心的是单标签的多分类问题，假设有$1,2,\cdots,K$共$K$个候选类别，训练数据为$(x,y)\sim\mathcal{D}$，建模的分布为$p_{\theta}(y|x)$，那么我们的优化目标是最大似然，或者说最小化交叉熵，即
\begin{equation}\mathop{\text{argmin}}_{\theta}\,\mathbb{E}_{(x,y)\sim\mathcal{D}}[-\log p_{\theta}(y|x)]\end{equation}
通常来说，我们建立的概率模型最后一步都是softmax，假设softmax之前的结果为$f(x;\theta)$（即logits），那么
\begin{equation}-\log p_{\theta}(y|x)=-\log \frac{e^{f_y(x;\theta)}}{\sum\limits_{i=1}^K e^{f_i(x;\theta)}}=\log\left[1 + \sum_{i\neq y}e^{f_i(x;\theta) - f_y(x;\theta)}\right]\label{eq:loss-1}\end{equation}
所谓类别不均衡，就是指某些类别的样本特别多，就好比“20%的人占据了80%的财富”一样，剩下的类别数很多，但是总样本数很少，如果从高到低排序的话，就好像带有一条很长的“尾巴”，所以叫做长尾现象。这种情况下，我们训练的时候采样一个batch，很少有机会采样到低频类别，因此很容易被模型忽略了低频类。但评测的时候，通常我们又更关心低频类别的识别效果，这便是矛盾之处。

常见思路 #

常见的思路大家应该也有所听说，大概就是三个方向：

1、从数据入手，通过过采样或降采样等手段，使得每个batch内的类别变得更为均衡一些；

2、从loss入手，经典的做法就是类别$y$的样本loss除以类别出现的频率$p(y)$；

3、从结果入手，对正常训练完的模型在预测阶段做些调整，更偏向于低频类别，比如正样本远少于负样本，我们可以把预测结果大于0.2（而不是0.5）都视为正样本。

Google的原论文中对这三个方向的思路也列举了不少参考文献，有兴趣调研的读者可以直接阅读原论文，另外，知乎上的文章《Long-Tailed Classification (2) 长尾分布下分类问题的最新研究》也对该问题进行了介绍，读者也可以参考阅读。

学习互信息 #

回想一下，我们是怎么断定某个分类问题是不均衡的呢？显然，一般的思路是从整个训练集里边统计出各个类别的频率$p(y)$，然后发现$p(y)$集中在某几个类别中。所以，解决类别不平衡问题的重点，就是如何把这个先验知识$p(y)$融入模型之中。

在之前构思词向量模型（如文章《更别致的词向量模型(二)：对语言进行建模》）的时候，我们就强调过，相比拟合条件概率，如果模型能直接拟合互信息，那么将会学习到更本质的知识，因为互信息才是揭示核心关联的指标。但是拟合互信息没那么容易训练，容易训练的是条件概率，直接用交叉熵$-\log p_{\theta}(y|x)$进行训练就行了。所以，一个比较理想的想法就是：如何使得模型依然使用交叉熵为loss，但本质上是在拟合互信息？

在公式$\eqref{eq:loss-1}$中，我们是建模了
\begin{equation}p_{\theta}(y|x)=\frac{e^{f_y(x;\theta)}}{\sum\limits_{i=1}^K e^{f_i(x;\theta)}}\end{equation}
现在我们改为建模互信息，那么也就是希望
\begin{equation}\log \frac{p_{\theta}(y|x)}{p(y)}\sim f_y(x;\theta)\quad \Leftrightarrow\quad \log p_{\theta}(y|x)\sim f_y(x;\theta) + \log p(y)\end{equation}
按照右端的形式重新进行softmax归一化，那么就有$p_{\theta}(y|x)=\frac{e^{f_y(x;\theta)+\log p(y)}}{\sum\limits_{i=1}^K e^{f_i(x;\theta)+\log p(i)}}$，或者写成loss形式：
\begin{equation}-\log p_{\theta}(y|x)=-\log \frac{e^{f_y(x;\theta)+\log p(y)}}{\sum\limits_{i=1}^K e^{f_i(x;\theta)+\log p(i)}}=\log\left[1 + \sum_{i\neq y}\frac{p(i)}{p(y)}e^{f_i(x;\theta) - f_y(x;\theta)}\right]\label{eq:loss-2}\end{equation}
原论文称之为logit adjustment loss。如果更加一般化，那么还可以加个调节因子$\tau$：
\begin{equation}-\log p_{\theta}(y|x)=-\log \frac{e^{f_y(x;\theta)+\tau\log p(y)}}{\sum\limits_{i=1}^K e^{f_i(x;\theta)+\tau\log p(i)}}=\log\left[1 + \sum_{i\neq y}\left(\frac{p(i)}{p(y)}\right)^{\tau}e^{f_i(x;\theta) - f_y(x;\theta)}\right]\label{eq:loss-3}\end{equation}
一般情况下，$\tau=1$的效果就已经接近最优了。如果$f_y(x;\theta)$的最后一层有bias项的话，那么最简单的实现方式就是将bias项初始化为$\tau\log p(y)$。也可以写在损失函数中：

import numpy as np
import keras.backend as K


def categorical_crossentropy_with_prior(y_true, y_pred, tau=1.0):
    """带先验分布的交叉熵
    注：y_pred不用加softmax
    """
    prior = xxxxxx  # 自己定义好prior，shape为[num_classes]
    log_prior = K.constant(np.log(prior + 1e-8))
    for _ in range(K.ndim(y_pred) - 1):
        log_prior = K.expand_dims(log_prior, 0)
    y_pred = y_pred + tau * log_prior
    return K.categorical_crossentropy(y_true, y_pred, from_logits=True)


def sparse_categorical_crossentropy_with_prior(y_true, y_pred, tau=1.0):
    """带先验分布的稀疏交叉熵
    注：y_pred不用加softmax
    """
    prior = xxxxxx  # 自己定义好prior，shape为[num_classes]
    log_prior = K.constant(np.log(prior + 1e-8))
    for _ in range(K.ndim(y_pred) - 1):
        log_prior = K.expand_dims(log_prior, 0)
    y_pred = y_pred + tau * log_prior
    return K.sparse_categorical_crossentropy(y_true, y_pred, from_logits=True)

结果分析 #

很明显logit adjustment loss也属于调整loss方案之一，不同的是它是在$\log$里边调整权重，而常规的思路则是在$\log$外调整。至于它的好处，就是互信息的好处：互信息揭示了真正重要的关联，所以给logits补上先验分布的bias，能让模型做到“能靠先验解决的就靠先验解决，先验解决不了的本质部分才由模型解决”。

在预测阶段，根据不同的评测指标，我们可以制定不同的预测方案。从《函数光滑化杂谈：不可导函数的可导逼近》可以知道，对于整体准确率而言，我们有近似
\begin{equation}\text{整体准确率} \approx \frac{1}{N}\sum_{i=1}^N p_{\theta}(y_i|x_i)\end{equation}
其中$\{(x_i,y_i)\}_{i=1}^N$是验证集。所以如果不考虑类别不均衡情况，追求更高的整体准确率，那么对于每个$x$我们直接输出$p_{\theta}(y|x)$最大的类别即可。但如果我们希望每个类的准确率都尽可能高，那么我们将上式改写成
\begin{equation}\text{整体准确率} \approx \frac{1}{N}\sum_{i=1}^N \frac{p_{\theta}(y_i|x_i)}{p(y_i)}\times p(y_i)=\sum_{y=1}^K p(y)\left(\frac{1}{N}\sum_{x_i\in\Omega_y} \frac{p_{\theta}(y|x_i)}{p(y)}\right)\end{equation}
其中$\Omega_y=\{x_i|y_i=y,i=1,2,\cdots,N\}$，也标签为$y$的$x$的集合，等号右边事实上就是先将同一个$y$的项合并起来。我们知道“整体准确率=每一类的准确率的加权平均”，而上式正好具有同样的形式，所以括号里边的$\frac{1}{N}\sum\limits_{x_i\in\Omega_y} \frac{p_{\theta}(y|x_i)}{p(y)}$就是“每一类的准确率”的一个近似了，因此，如果我们希望每一类的准确率都尽可能高，我们则要输出使得$\frac{p_{\theta}(y|x)}{p(y)}$最大的类别（不加权）。结合$p_{\theta}(y|x)$的形式，我们有结论
\begin{equation}y^{*}=\left\{\begin{aligned}&\mathop{\text{argmax}}\limits_y\, f_y(x;\theta)+\tau\log p(y),\quad(\text{追求整体准确率})\\
&\mathop{\text{argmax}}\limits_y\, f_y(x;\theta),\quad(\text{希望每一类的准确率都尽可能均匀})
\end{aligned}\right.\end{equation}
第一种其实就是输出条件概率最大者，而第二种就是输出互信息最大者，按具体需求选择。

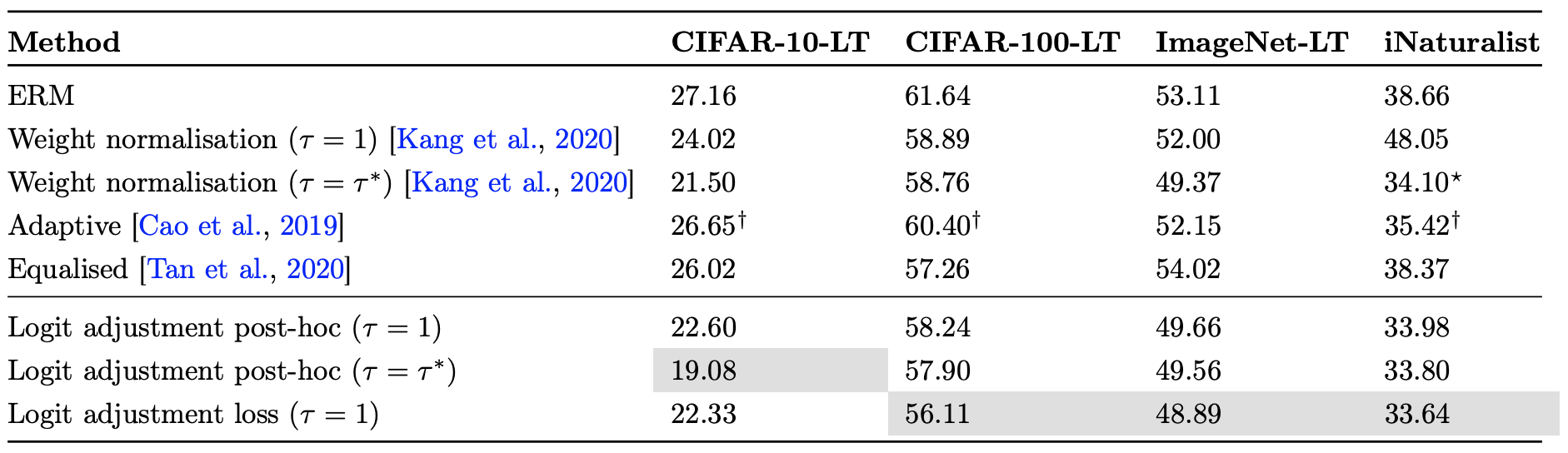
至于详细的实验结果，大家可以自行看论文，总之就是好到有点意外：

原论文的实验结果

文章小结 #

本文简单介绍了一种基于互信息思想的类别不平衡处理办法，该方案以前笔者也曾经构思过，不过没有深究，而最近Google的一篇论文也给出了同样的方法，遂在此简单记录分析一下，最后Google给出的实验结果显示该方法能达到SOTA的水平。

转载到请包括本文地址：https://spaces.ac.cn/archives/7615

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。