《自然极值》系列——4.费马点问题

通过上面众多的文字描述，也许你还不大了解这两个原理有何美妙之处，也或者你已经迫不及待地想去应用它们却不知思路。为了不至于让大家产生“审美疲劳”，接下来我们将试图利用这两个原理对费马点问题进行探讨，看看原理究竟是怎么发挥作用的。运用的关键在于：如何通过适当的变换将其与光学或势能联系起来。

传统费马点问题是指在ΔABC中寻找点P，使得$AP+BP+CP$最小的问题；而广义的费马点则改成使$k_1 AP+k_2 BP+k_3 CP$最小。这是很具有现实意义的，是“在三个村庄之间建立一个中转站，如何才能使运送成为最低”之类的最优问题。我们将从光学和势能两个角度对这个问题进行探讨（也许有的读者已经阅读过了利用重力的原理来求解费马点，但是我想光学的方法依然会是你眼前一亮的。）

一、“光解”费马点

我们发现广义费马点中所求的$kAP+mBP+nCP$与折射定律中$\frac{PO}{v_1}+\frac{QO}{v_2}$在形式上十分相似，于是我们想到可以应用折射定律。首先将其改成
$$\frac{AP}{(1/{k_1})}+\frac{BP}{(1/{k_2})}+\frac{CP}{(1/{k_3})},v_1=1/{k_1},v_2=1/{k_2},v_3=1/{k_3}$$

费马原理是关于两者和的极值，而费马点是三项的。为了能够应用费马原理，我们需要先“定”一个长度。如下图：

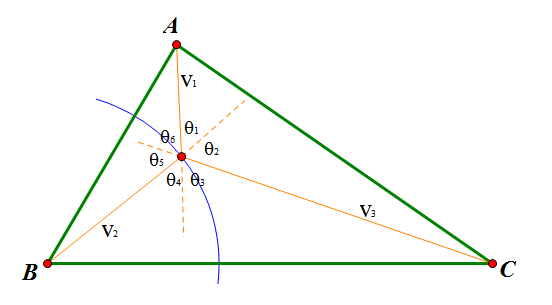
假定已经给出BP长度，那么我们以它为半径作圆弧，并假设圆弧就是一面特别的反射镜（经它反射后光速会变）。于是我们的问题就变成了：从圆弧上找出P点，使得$k_1 AP+k_3 CP$最短。

根据费马原理，我们要选择光路。这个光路就是我们在前边“费马原理”一小节中所得到的“折反射定律”推论，即令
$$\frac{\sin \theta_1}{v_1}=\frac{\sin\theta_2}{v_3}\Rightarrow k_1 \sin\theta_1=k_3 \sin\theta_2$$

同样可以将BP换成AP、CP进行如上设置，即有
$$\begin{aligned}k_3 \sin\theta_3=k_2 \sin\theta_4 \\ k_2 \sin\theta_5=k_1 \sin\theta_6\end{aligned}$$

根据“对顶角相等”以及“相邻三个角之和为π ”，即得

$$\begin{aligned}\frac{\sin\theta_1}{k_3}=\frac{\sin\theta_5}{k_1};\frac{\sin\theta_3}{k_2}=\frac{\sin\theta_1}{k_3};\frac{\sin\theta_5}{k_1}=\frac{\sin\theta_3}{k_2} \\ \theta_1+\theta_3+\theta_5=\pi\end{aligned}$$

可见，$\theta_1,\theta_3,\theta_5$正是以$k_3,k_2,k_1$为对边的三角形的三个内角。至此，BoJone认为问题已经解决。剩下的细节将留给各位思考（不应该将所有的奥妙都揭示出来，因为这样未免过于单调了）。

二、“势解”费马点

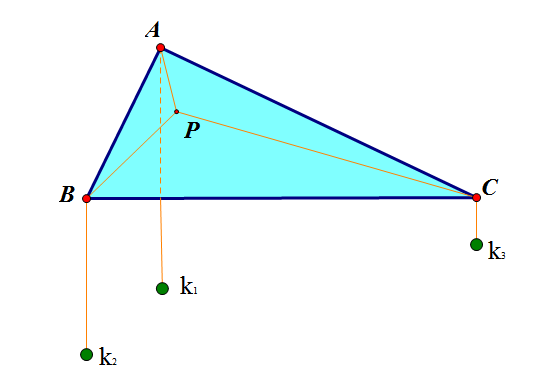
设想将ΔABC水平放置，高度为h；将三条长度为l的绳子一端系在一起，另一端分别系一个重$k_1,k_2,k_3$的重物。如图，使他们必须分别穿过A、B、C三点。

在重力作用下，它们会趋于平衡状态，即势能最小，即要求$k_1 [h-(l-AP)]+k_2 [h-(l-BP)]+k_3 [h-(l-CP)]$最小（重力势能$E_p=Gh$，中括号内分别正是每个重物的高度），等价于$k_1 AP+k_2 BP+k_3 CP$最小。

由平衡态公理，稳定后三者受力平衡，即三条绳子的结点处合外力应该为0。于是我们得到了求解答案：它既可以写成我们在“光解”时的形式，也可以为了计算的方便写成：

$k_1^2+k_2^2+2k_1 k_2 cos\angle APB=k_3^2$（力的平行四边形法则）

其他两个类似，不再赘述。至此，两个角度，两种解法，一个问题，OK！

多谈一点：

不论是费马原理还是平衡态公理，都是物理的极值，读者需要运用你们的非凡想象力，将数学极值问题与其联系起来。当然，这个方法并不是万能的，因为它们本来就不是为数学研究准备的。我们研究它们，是为了领略科学之美，方便我们的计算和解答，并企图做出一些新的发现。而系统化、精细化的工作，并不是我们的任务（当然，有兴趣的朋友也可以去完成）

附上一道比较有趣的题目，读者可以运用这两个原理进行思考解答：

找出锐角三角形的内接三角形中周长最短者。

欢迎各位读者思考！

转载到请包括本文地址：https://spaces.ac.cn/archives/1076

更详细的转载事宜请参考：《科学空间FAQ》