物理学的美不仅仅表现在简洁的公式上。我们还惊奇地发现，很多物理现象都是按照使某个变量达到极值的方式发生。一个典型的例子就是费马原理，它指出了光的传播路径的一个重要规律：光总是沿着所花时间最短的路径传播。这里我们将简单介绍一下费马原理。

费马原理俗称“最快到达原理”、“最小时间原理”。1657年，费马提出：

从P点到达Q点，在所有可行的路径中，光选择了所需时间最短的一条。
从P点到达Q点，在所有可行的路径中，光选择了所需时间为极值的一条。

这是一个极其奇妙的原理，也是自然界中最神奇的极值之一。作为非生物的光，居然自主地选择了最优路径，成为世界上“效率最高”的东西，这让人不得不佩服宇宙的伟大。这究竟是造物者的精心设计，还是无心之作？

费马原理主要体现在：

1、光速是宇宙中最快的速度
2、光沿着直线传播（均匀介质）
3、光的反射定律
4、光的折射定律（Snell定律）

其中(1)是物理学上的内容，我们不去讨论它；而(2)和(3)则是我们相对熟悉的内容，即便是现在的初中生已经接触过了，因此也不再详细讨论，我们只稍微谈一下(4)，并可以发现：(2)和(3)均是(4)的结论。

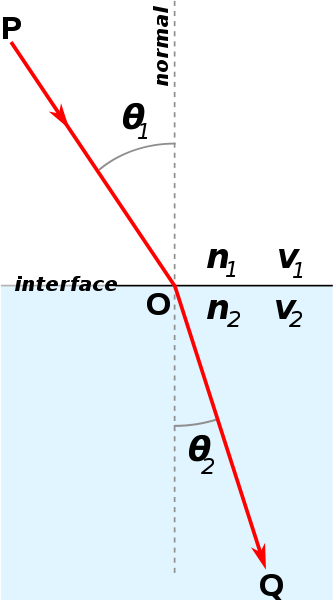
Snell定律

Snell定律

如图，在直线inteface上有动点O，并有两定点P和Q，使$\frac{PO}{v_1}+\frac{QO}{v_2}$最小的充要条件是$\frac{v_1}{\sin\theta_1}=\frac{v_2}{\sin\theta_2}$。

我们可以设$P=(x_1,y_1),Q=(x_2,y_2),O=(x,0)$，则
$$t=\frac{\sqrt{(x_1-x)^2+y_1^2}}{v_1}+\frac{\sqrt{(x_2-x)^2+y_2^2}}{v_2}$$
对其求导并令其为0得
$$0=\frac{x-x_1}{v_1 \sqrt{(x_1-x)^2+y_1^2}}+\frac{x-x_2}{v_2 \sqrt{(x_2-x)^2+y_2^2}}$$
即
$$\frac{v_1}{\sin\theta_1}=\frac{v_2}{\sin\theta_2}$$
证毕。

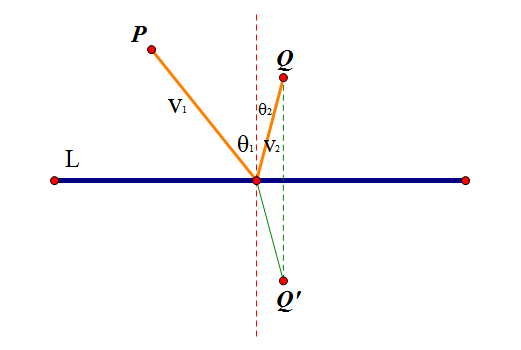
注意，在上述证明中，我们并没有谈到P,Q必须在inteface的两侧，因此，结论对于P,Q在同一侧也是成立的。也许下面的图可以帮助你更好的理解这一点（通过镜面对称的方式，变成光的折射问题，你是不是感觉这种方法有点熟悉呢？）

折射定律-推论

折射定律-推论

为了方便引用，我们姑且将P,Q在同一侧情况的Snell定律成为光的“折反射定律”吧。我们不难看到，光的直线传播和反射定律其实就是$v_1=v_2$时候的情况。要注意的是，虽然我们上面用到了“充要条件”这一名词，但那只是一个特殊的情况，在更多的情况里，费马原理只是一个“必要条件”。在这一篇文章里头，我们稍稍地对光的传播和光路最快做了一个论证，为接下来的应用奠好基础。不过，接着并非要马上谈到光学原理的应用，而是先把目光转移，集中到另外一个“自然极值”上边去，它和我们平时看到的很多现象有关...

转载到请包括本文地址：https://spaces.ac.cn/archives/1068

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Nov. 27, 2010). 《《自然极值》系列——2.费马原理 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/1068

@online{kexuefm-1068,
        title={《自然极值》系列——2.费马原理},
        author={苏剑林},
        year={2010},
        month={Nov},
        url={\url{https://spaces.ac.cn/archives/1068}},
}