农村的孩子免不了常做家务，当然我家也没有什么特别沉重的家务，通常都是扫地、做饭、洗菜这些简单的活儿。说到洗菜，洗完菜后总喜欢边放水边搅水，然后就在水面上形成一个颇为有趣的漩涡。现在我们从数学物理的角度来分析一下这个漩涡。

在讲洗手盆的漩涡之前，我们先来看一下一个比较类似的、更古老的问题——牛顿的旋转液面问题。牛顿假设有一个水桶（假设为圆柱形吧，但这不重要），水桶在绕自己的中轴线匀角速度旋转，直到桶内的水也随着匀角速度旋转（即水与水桶相对静止），此时水的液面形状是凹的，我们来看看该液面的形状。

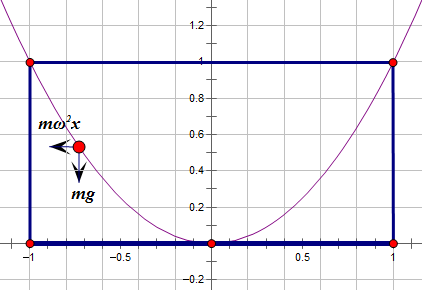
牛顿的水桶

要分析形状，我们还要回顾之前提到过的流体静力学平衡：
http://kexue.fm/archives/1964/

该定律告诉我们当流体达到平衡状态时，所受合外力必然与液面垂直。有了这个就相当好办了，取液面上的一滴小水珠，设其质量为m，它受到两个力的作用：地球的重力以及旋转产生的离心力。如图所示：

旋转的水桶

旋转的水桶

离心力：$m\omega^2 x$
重力：$mgy$
切向量：$(dx,dy)$

垂直就意味着：$\frac{dy}{dx}=\tan\theta=\frac{m\omega^2 x}{mg}=\frac{\omega^2 x}{g}$

解得$y=\frac{\omega^2}{2g}x^2$

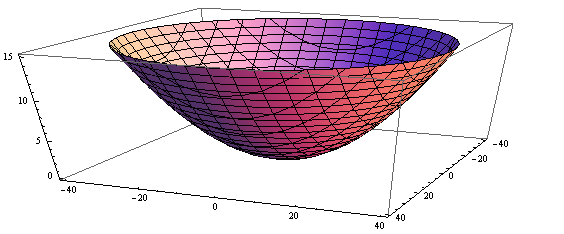
即这是一个旋转抛物面！

旋转抛物面

旋转抛物面

抛物面，读者能够联想到什么呢？天文爱好者应该不难联想到“牛反”！对，就是牛顿反射望远镜，它的主镜面也是旋转抛物面，只不过它一般是用固体制作的。其实当初牛顿发现这是一个旋转抛物面时，也曾想过用旋转的汞来做望远镜的镜面，但是一直以来各种干扰难以克服（稍微一晃就变形了），所以仅限于纸面上。然而随着技术的发展，这种旋转液面望远镜已经面世了，而且前景一片美好。

以下信息源自互联网：

世界上第一架液体望远镜是在20世纪50年代初，由苏联物理学家乌德用一盆水银布制成的。经过不断改进探索，加拿大科学家阿曼罗·博拉在80年代初制造出了第一架可供天文观测用的液体望远镜，镜头直径为45厘米。后来，博拉又用250千克水银制成了两台直径1米、一台直径1.6米的望远镜，并在水银面上加了一层特殊的透明树脂，既解决了外界因素对水银面的干扰，又避免了水银蒸发从而危害人体健康的问题。

1995年，美国航天局造出了直径3米的水银望远镜，安装在新墨西哥州，专门监视太空垃圾和近地小行星。其总成本不到50万美元，而通常像这样大小的望远镜制作费用至少为一二千万美元。

回到洗手盆

有生活经验的朋友会发现，洗手盆水所形成的漩涡明显不是旋转抛物面的，原因很简单，洗手盆的水经过搅动后还没有形成整体匀角速度旋转，仔细观察就会发现，它更像是整体匀速旋转。也就是说，速度大小是固定的，接近中心处角速度大些，较远处角速度小一些。这样我们只要把离心力这一项换成$\frac{m v^2}{x}$就行了，得到：

$$\frac{dy}{dx}=\tan\theta=\frac{\frac{m v^2}{x}}{mg}=\frac{v^2}{gx}$$

解得
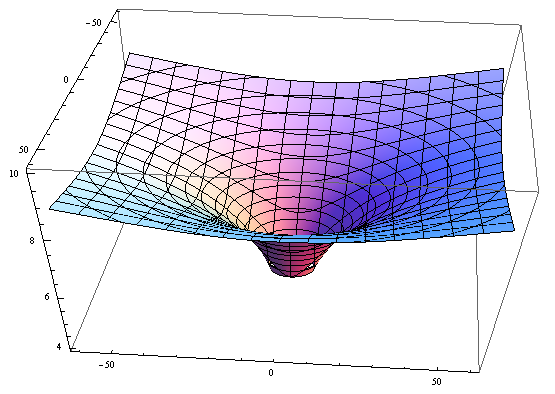
$$y=\frac{v^2}{g} ln x$$

这是一条对数曲线，将它绕y轴旋转时候就得到了大概的形状，画出来如下图

洗手盆液面

洗手盆液面

虽然不尽合理（没有与y轴相交的点），但显然这更接近我们所观察到的样子。

转载到请包括本文地址：https://spaces.ac.cn/archives/2031

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Jul. 20, 2013). 《洗手盆里的学问 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/2031

@online{kexuefm-2031,
        title={洗手盆里的学问},
        author={苏剑林},
        year={2013},
        month={Jul},
        url={\url{https://spaces.ac.cn/archives/2031}},
}