不可能事件——一道经典电磁感应题的错误
By 苏剑林 | 2011-01-09 | 36703位读者 |相信高二理科的学生都会做过这样的一道题目:
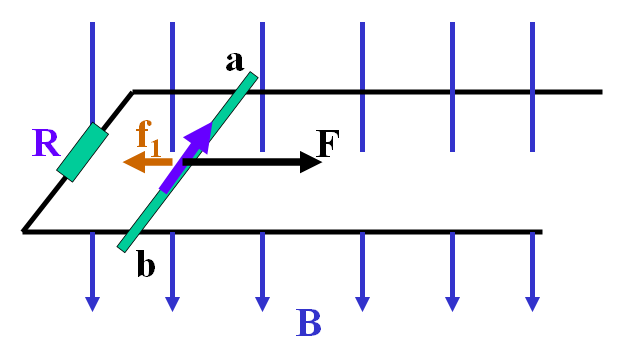
水平放置于匀强磁场中的光滑导轨上,磁感应强度为B,平衡导轨的距离为L,有一根导体棒ab,用恒力F作用在ab上,由静止开始运动,回路总电阻为R,求ab的最大速度。
对于高二学生来说,这样的题目是很好解决的。只要列出
$E=BLv,I=\frac{E}{R},f_1=BIL$,并根据当匀速运动时速度最大,由受力平衡有$f_1=F$,解得
(E:感应电动势;I:感应电流;f1:安培力)
$$v=\frac{FR}{B^2 L^2}$$
看似非常合理,可是BoJone在进一步分析这个问题时,却发现了很奇怪的现象:它根本不可能达到匀速运动状态!
我们从高等数学角度分析一下这个问题。设ab质量为m,其受力是$F-f_1=F-BIL=F-\frac{B^2 L^2 v}{R}$,由牛顿第二定律得到$ma=F-\frac{B^2 L^2 v}{R}$,记$p=\frac{F}{m},q=\frac{B^2 L^2 }{mR}$,得到
$$\ddot{s}=p-q\dot{s}$$
这是一个二阶微分方程,积分一次就得到$\dot{s}=pt-qs+C_1$,并且开始时候位移和速度都为0,有$C_1=0$
解方程$\dot{s}=pt-qs$得:
$$s = C_2 e^{-q t}+\frac{p}{q}t-\frac{p}{q^2}$$
同样根据开始时候位移为0得到$C_2=\frac{p}{q^2}$,于是就有
$$v=\dot{s}=\frac{p}{q}(1-e^{-qt})$$
显然,最大速度为$V_{max}=\frac{p}{q}=\frac{FR}{B^2 L^2}$,结果和高中的经典做法一样。可是,我们惊讶地发现,这个结果的取值,需要$t \to \infty$。换句话说,根本就达不到这个状态!
思考
显然,这个例子说明了教材的命题者并没有经过进一步的思考,草率地出了这一道题目,犯了“想当然”的错误。BoJone不禁提出一个疑问:对于一个中国高中生来说,进行上述分析的确过于苛刻,但是对于一个教材命题者来说,上述过程显然是可以轻而易举地完成的(受力分析,解答二阶线性微分方程),但为什么这一道“谬题”一出再出?难道功利性足以掩盖科学的严谨性?还是高中物理不需要严谨?还是欺负高中生不懂数学分析而随便“蒙混过关”?(BoJone承认,这评论过激了,抱歉...)
另一方面,这也告诉我们,不能盲目迷信权威。当我们拥有了更充足的科学知识时,不妨回头看看,对我们曾经“解决”过的问题进行再次分析,或许会有意外的收获!
后注:
物理定律始终有个精确度和适用范围问题,虽然本题的时间为无穷大,但是只要给定精确度,就存在一个有限大的时间内可以达到这个精确度,因此本题也无可厚非。本文(原文)写于高中的“血气方刚”之时,正好发现这现象,稍微激动了一些。也正是因为这道题,让我对物理的意义了解更为深入了一些。正所谓人生处处皆学问呀。(2011.02.12)
转载到请包括本文地址:https://spaces.ac.cn/archives/1170
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jan. 09, 2011). 《不可能事件——一道经典电磁感应题的错误 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/1170
@online{kexuefm-1170,
title={不可能事件——一道经典电磁感应题的错误},
author={苏剑林},
year={2011},
month={Jan},
url={\url{https://spaces.ac.cn/archives/1170}},
}










January 9th, 2011
站长啊,这个问题说是错误有些过了,至少不值得因此对教育进行一番“批判”,特别是受到高中水平的限制。物理学中这样类似的问题有很多,例如物体在粘滞流体中最终会做匀速运动,密立根还利用这个原理去测原电荷大小。之所以能这样做是因为在很多情况下只需要不是非常长的时间就可以几乎认为达到最大速度做匀速运动,这是一种近似的思想,而且是一种相当好的近似。
January 9th, 2011
这其实就是一种模型。模型就是一种近似,如果近似合理就有存在的价值。模型在物理学中是非常重要的概念,例如伽利略在研究自由落体运动时忽略空气阻力就是一种模型,听说当时这种模型还被质疑过,但是很明显这个模型是合理的,只要合理,就不能说是错误。建立模型的目的在于简化,你看你算了那么多才把结果算出来,而简化后的模型解法非常简单,这就是模型的作用。
我承认此评论过激了,呵呵,收回。原谅小孩子的意气用事,呵呵
January 11th, 2011
同意一楼二楼。
February 3rd, 2011
哈哈,我是高三的.其实类似的高中物理问题还有很多
汽车启动,功率恒定那种方式,最大速度不可达到
上述问题的变形:给ab初速度而不是恒力.停下时发出Q热量,求停下时刻..呵呵
June 26th, 2011
能不能把你的音乐调成可以关了的,
我打开你好几个网页,好烦阿!
谢谢!
你的网页做的很好。
学到很多。
谢谢你的支持,只是我记得应该有暂停按钮的...