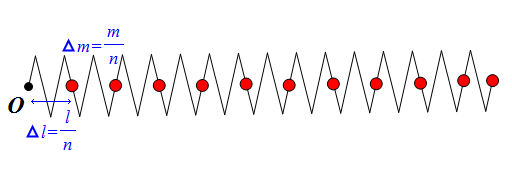
一维弹簧的运动(下)
By 苏剑林 | 2014-03-13 | 34034位读者 | 引用在上一篇文章中,我们得到了一维弹簧运动的方程
$$m\frac{\partial^2 X}{\partial t^2}=k\frac{\partial^2 X}{\partial \xi^2}$$
并且得到了通解
$$X=F(u)+H(v)=F(\xi+\beta t)+H(\xi-\beta t)$$
或者
$$X(\xi,t)=\frac{1}{2}\left[X_0(\xi+\beta t)+X_0(\xi-\beta t)\right]+\frac{1}{2\beta}\int_{\xi-\beta t}^{\xi+\beta t} X_1 (s)ds$$
在文章的末尾,提到过这个解是有些问题的。现在让我们来详细分析它。
一维弹簧的运动(上)
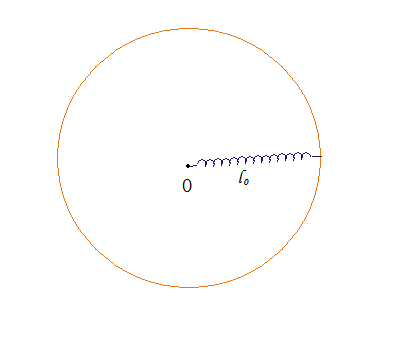
By 苏剑林 | 2014-03-11 | 37605位读者 | 引用重提“旋转弹簧伸长”问题(变分解法)
By 苏剑林 | 2011-04-05 | 23904位读者 | 引用感谢Awank-Newton读者的来信,本文于2013.01.30作了修正,主要是弹性势能的正负号问题。之前连续犯了两个错误,导致得出了正确答案。现在已经修正。参考《平衡态公理的修正与思考》
在下面的两篇文章中,BoJone已经介绍了这个“旋转弹簧伸长”的问题,并从两个角度提供了两种解答方法。前者列出了一道积分方程,然后再转变为微分方程来解;后者直接从弹性力学的角度来列出一道二阶微分方程,两者殊途同归。
http://kexue.fm/archives/782/
今天,再经过一段时间的变分法涉猎后,BoJone尝试从变分的角度(总能量最小)来给出一种新的解法。同样设r为旋转达到平衡后弹簧上一点到旋转中心的距离,该点的线密度为$\lambda =\lambda (r)$,该点到中心的弹簧质量为$m=m(r)$,旋转前的长度为$l_0$,旋转平衡后的长度为$l_1$。由于弹簧旋转后已经达到了平衡状态,由平衡态公理(参看《自然极值》系列),平衡意味着总能量“动能-势能”取极值。









最近评论