科学空间|Scientific Spaces

最近一直在考虑一些自然语言处理问题和一些非线性分析问题，无暇总结发文，在此表示抱歉。本文要说的是对于一阶非线性差分方程（当然高阶也可以类似地做）的一种摄动格式，理论上来说，本方法可以得到任意一阶非线性差分方程的显式渐近解。

非线性差分方程

对于一般的一阶非线性差分方程
$$\begin{equation}\label{chafenfangcheng}x_{n+1}-x_n = f(x_n)\end{equation}$$
通常来说，差分方程很少有解析解，因此要通过渐近分析等手段来分析非线性差分方程的性质。很多时候，我们首先会考虑将差分替换为求导，得到微分方程
$$\begin{equation}\label{weifenfangcheng}\frac{dx}{dn}=f(x)\end{equation}$$
作为差分方程$\eqref{chafenfangcheng}$的近似。其中的原因，除了微分方程有比较简单的显式解之外，另一重要原因是微分方程$\eqref{weifenfangcheng}$近似保留了差分方程$\eqref{chafenfangcheng}$的一些比较重要的性质，如渐近性。例如，考虑离散的阻滞增长模型：
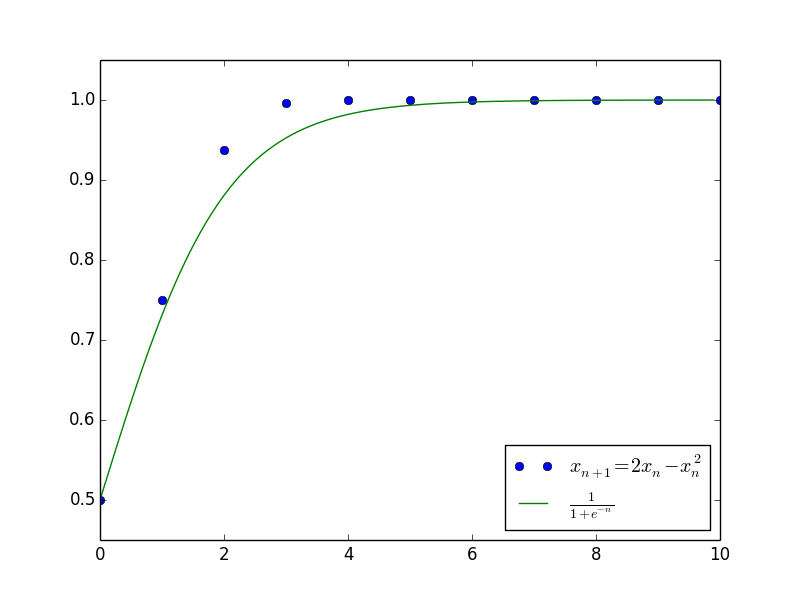
$$\begin{equation}\label{zuzhizengzhang}x_{n+1}=(1+\alpha)x_n -\beta x_n^2\end{equation}$$
对应的微分方程为（差分替换为求导）：
$$\begin{equation}\frac{dx}{dn}=\alpha x -\beta x^2\end{equation}$$
此方程解得
$$\begin{equation}x_n = \frac{\alpha}{\beta+c e^{-\alpha n}}\end{equation}$$
其中$c$是任意常数。上述结果已经大概给出了原差分方程$\eqref{zuzhizengzhang}$的解的变化趋势，并且成功给出了最终的渐近极限$x_n \to \frac{\alpha}{\beta}$。下图是当$\alpha=\beta=1$且$c=1$（即$x_0=\frac{1}{2}$）时，微分方程的解与差分方程的解的值比较。

差分方程的摄动法1

现在的问题是，既然微分方程的解可以作为一个形态良好的近似解了，那么是否可以在微分方程的解的基础上，进一步加入修正项提高精度？

点击阅读全文...

问题来源

笔者经常学习的数学研发论坛曾有一帖讨论下述非线性差分方程的渐近求解：
$$a_{n+1}=a_n+\frac{1}{a_n^2},\, a_1=1$$
原帖子在这里，从这帖子中我获益良多，学习到了很多新技巧。主要思路是通过将两边立方，然后设$x_n=a_n^3$，变为等价的递推问题：
$$x_{n+1}=x_n+3+\frac{3}{x_n}+\frac{1}{x_n^2},\,x_1=1$$
然后可以通过巧妙的技巧得到渐近展开式：
$$x_n = 3n+\ln n+a+\frac{\frac{1}{3}(\ln n+a)-\frac{5}{18}}{n}+\dots$$
具体过程就不提了，读者可以自行到上述帖子学习。

然而，这种形式的解虽然精妙，但存在一些笔者不是很满意的地方：

1、解是渐近的级数，这就意味着实际上收敛半径为0；
2、是$n^{-k}$形式的解，对于较小的$n$难以计算，这都使得高精度计算变得比较困难；
3、当然，题目本来的目的是渐近计算，但是渐近分析似乎又没有必要展开那么多项；
4、里边带有了一个本来就比较难计算的极限值$a$；
5、求解过程似乎稍欠直观。

当然，上面这些缺点，有些是鸡蛋里挑骨头的。不过，也正是这些缺点，促使我寻找更好的形式的解，最终导致了这篇文章。

点击阅读全文...