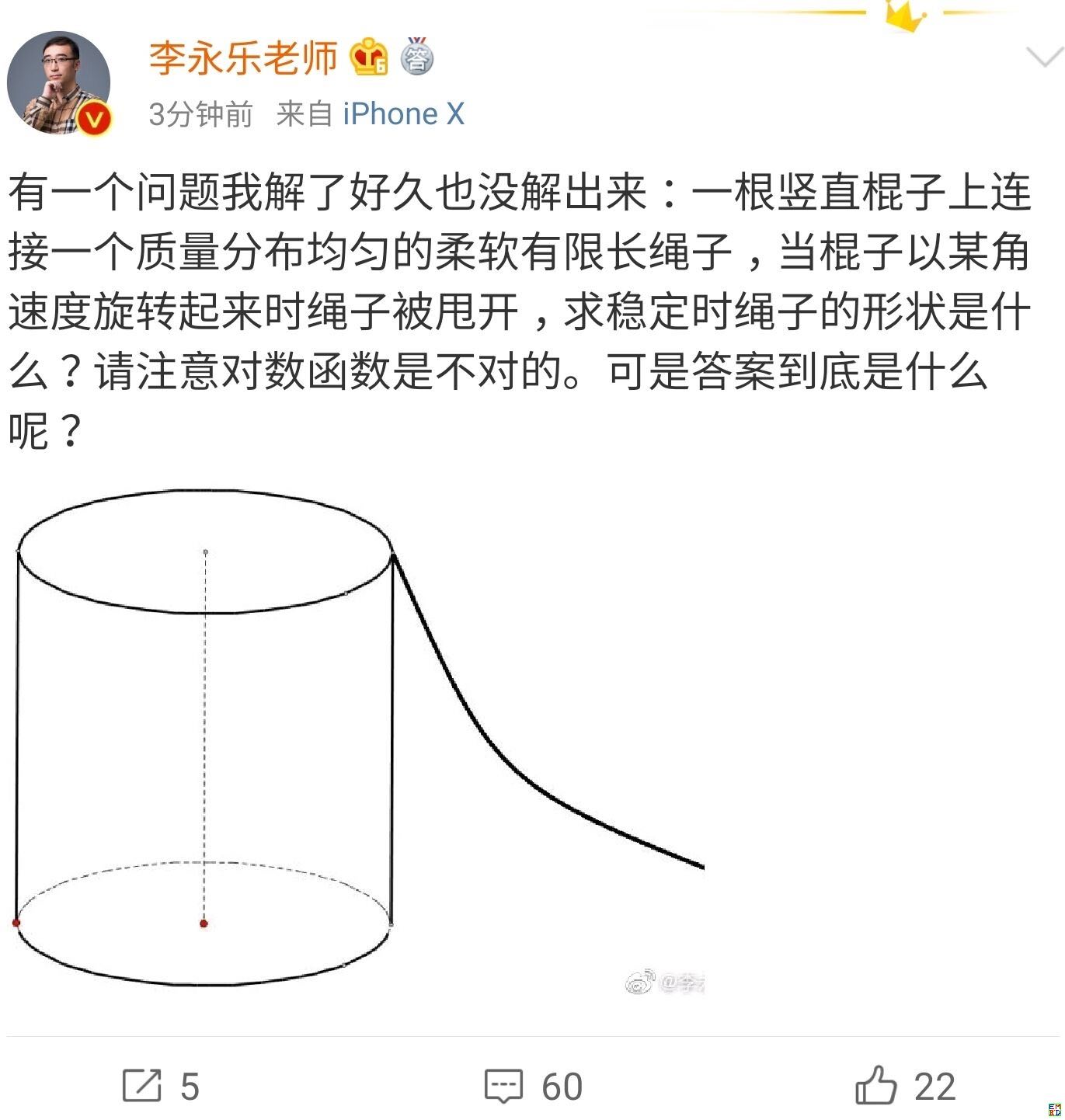
你跳绳的时候,想过绳子的形状曲线是怎样的吗?
By 苏剑林 | 2019-07-06 | 65839位读者 | 引用【理解黎曼几何】8. 处处皆几何 (力学几何化)
By 苏剑林 | 2016-11-02 | 71532位读者 | 引用黎曼几何在广义相对论中的体现和应用,虽然不能说家喻户晓,但想必大部分读者都有所听闻。一谈到黎曼几何在物理学中的应用,估计大家的第一反应就是广义相对论。常见的观点是,广义相对论的发现大大推动了黎曼几何的发展。诚然,这是事实,然而,大多数人不知道的事,哪怕经典的牛顿力学中,也有黎曼几何的身影。
本文要谈及的内容,就是如何将力学几何化,从而使用黎曼几何的概念来描述它们。整个过程事实上是提供了一种框架,它可以将不少其他领域的理论纳入到黎曼几何体系中。
黎曼几何的出发点就是黎曼度量,通过黎曼度量可以通过变分得到测地线。从这个意义上来看,黎曼度量提供了一个变分原理。那反过来,一个变分原理,能不能提供一个黎曼度量呢?众所周知,不少学科的基础原理都可以归结为一个极值原理,而有了极值原理就不难导出变分原理(泛函极值),如物理中就有最小作用量原理、最小势能原理,概率论中有最大熵原理,等等。如果有一个将变分原理导出黎曼度量的方法,那么就可以用几何的方式来描述它。幸运的是,对于二次型的变分原理,是可以做到的。
ODE的坐标变换
熟悉理论力学的读者应该能够领略到变分法在变换坐标系中的作用。比如,如果要将下面的平面二体问题方程
$$\left\{\begin{aligned}\frac{d^2 x}{dt^t}=\frac{-\mu x}{(x^2+y^2)^{3/2}}\\
\frac{d^2 y}{dt^t}=\frac{-\mu y}{(x^2+y^2)^{3/2}}\end{aligned}\right.\tag{1}$$
变换到极坐标系下,如果直接代入计算,将会是一道十分繁琐的计算题。但是,我们知道,上述方程只不过是作用量
$$S=\int \left[\frac{1}{2}\left(\dot{x}^2+\dot{y}^2\right)+\frac{\mu}{\sqrt{x^2+y^2}}\right]dt\tag{2}$$
变分之后的拉格朗日方程,那么我们就可以直接对作用量进行坐标变换。而由于作用量一般只涉及到了一阶导数,因此作用量的变换一般来说比较简单。比如,很容易写出,$(2)$在极坐标下的形式为
$$S=\int \left[\frac{1}{2}\left(\dot{r}^2+r^2\dot{\theta}^2\right)+\frac{\mu}{r}\right]dt\tag{3}$$
对$(3)$进行变分,得到的拉格朗日方程为
$$\left\{\begin{aligned}&\ddot{r}=r\dot{\theta}^2-\frac{\mu}{r^2}\\
&\frac{d}{dt}\left(r^2\dot{\theta}\right)=0\end{aligned}\right.\tag{4}$$
就这样完成了坐标系的变换。如果想直接代入$(1)$暴力计算,那么请参考《方程与宇宙》:二体问题的来来去去(一)
一维弹簧的运动(下)
By 苏剑林 | 2014-03-13 | 33417位读者 | 引用在上一篇文章中,我们得到了一维弹簧运动的方程
$$m\frac{\partial^2 X}{\partial t^2}=k\frac{\partial^2 X}{\partial \xi^2}$$
并且得到了通解
$$X=F(u)+H(v)=F(\xi+\beta t)+H(\xi-\beta t)$$
或者
$$X(\xi,t)=\frac{1}{2}\left[X_0(\xi+\beta t)+X_0(\xi-\beta t)\right]+\frac{1}{2\beta}\int_{\xi-\beta t}^{\xi+\beta t} X_1 (s)ds$$
在文章的末尾,提到过这个解是有些问题的。现在让我们来详细分析它。
一维弹簧的运动(上)
By 苏剑林 | 2014-03-11 | 36718位读者 | 引用在讨论了倒立单摆的相关分析之后,胡雄大哥(笔者的一位好友)提出了一个问题:一根均匀杆,当然质量不可忽略,只有一个力(简单起见,可以先假设为恒力)作用在其中一个点上(简单起见,可以假设为端点),那么杆是怎么运动的?
其实笔者学了不少的经典力学,也分析了不少问题,但就是对于力矩、角动量等还是模模糊糊的,对于我来说,大多数经典力学问题就是“作用量+变分”,本题也不例外。为了让题目的实验意义更加明确,不妨将题目改成:
一根中性的均匀杆,它的一个端点带有一个点电荷,那么它(仅仅)在一个均匀电场中的运动是怎样的?
在这里,我们进一步简化,只考虑平面问题。杆属于刚体,为了描述杆的运动,我们需要描述杆上一点的运动,以及杆绕这一点的转动,也就是说,即使只考虑平面的情况,该系统也是有三个自由度的。设杆的带电荷那一端点的坐标为$(x,y)$,为了描述杆的转动,以这一端点为中心建立极坐标系,设杆的极角为$\theta$。设电势的函数为$U(x,y)$,因为只有一点带电(受力),因此势能是简单的。
有质动力:倒立单摆的稳定性
By 苏剑林 | 2013-12-29 | 61429位读者 | 引用力学系统及其对偶性(三)
By 苏剑林 | 2013-11-15 | 20838位读者 | 引用在上一篇文章中,我已经初步地从最小作用量原理的角度来观察对偶定律的表现。虽然那是一种便捷有效的方法,但是还是给我们流下了一些遗憾。上一节是从几何形式的作用量原理出发的,而没有在一般形式的作用量框架下讨论。因为如果在$S=\int Ldt=\int (T-U)dt$的形式下讨论坐标变换问题会出现困难,困难源于我们进行了变换$d\tau=|z|^2 dt$,这导致了时间和空间的耦合,变分不能简单地进行。但是,这并非无法解决的问题。我们还是可以在基本的作用量原理之下讨论变换问题。下面将对此问题进行讨论。
变分中的变量代换
考虑一个一般的保守系统的作用量:
$$S=\int_{t_1}^{t_2} L(q,\frac{dq}{dt})dt$$








最近评论