科学空间|Scientific Spaces

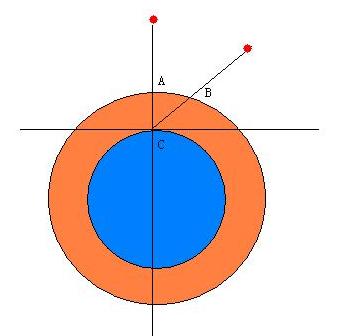
天文学中有一个名词Airmass，注意这并非Air mass（空气质量），这是指天顶距等于z的方向上大气光学厚度和天顶方向大气光学厚度之比，我目前也找不到它的中文名称究竟是什么，反正觉得如果译成“大气质量”很怪，就暂且翻译成“大气厚度指数”好了。现在知道它叫做“大气光学质量”了，一般用X表示，如下图中，$X={BC}/{AC}$。

星光传播示意图

在一片较小的区域内，大气层和地面都可以视为平行平面，这时有一个很好的近似公式：
$$X=\sec z$$
对于现在的中学教材来说，有的读者可能不了解\sec为何物，实际上：$\sec z=\frac{1}{\cos z}$

点击阅读全文...

cnao-jpg

最近计划搞一个“天文奥赛网”，希望能够藉此为天文爱好者参加天文奥赛提供方便，同时把天文爱好者联合起来，为大家提供一个交流学术的平台。在设计网站的过程中，打算把全国天文奥林匹克竞赛的Logo加上去，但是北京天文馆上提供的是JPG格式的，不便更换背景，需要透明背景的png格式才方便我们的编辑。而我这等平民又不善于PhotoShop，所以只得求助Google了。终于发现了一款小软件——RecomposIt！

点击阅读全文...

如果你已经安装了MathPlayer，就这里检查一下你的版本是否最新版：
http://www.dessci.com/en/products/mathplayer/check.htm

如果你还没有安装，欢迎你点击下面的链接下载安装：
http://www.dessci.com/en/products/mathplayer/download.htm

点击阅读全文...

冬夜星空

看了标题，也许你会发出疑问：这是哪位歌星的佳作？不过我得告诉你，别傻了，你知道哪位歌星是天文爱好者？这首纯属取材天文（星座、星空）的歌曲，来自于牧夫天文论坛，是一位ID为Turkish Cats的会员及其同伴创作的。 根据Turkish Cats在论坛上的活动，可以发现TC是一位音乐和天文的爱好者。TC把自己的天文情感融入到了音乐之中，写出了这首颇为优美柔和的歌曲。作为天文爱好者的BoJone，我很希望越来越多的人参与到天文中。其实并非一定是要作科学研究才可以参与天文，各行各业都是可以的，就像本歌曲的作者。相信我，你会在天文上获益匪浅！现在我们不妨来聆听下这美妙的旋律。

歌曲聆听（右端可以下载）：

点击阅读全文...

wilderness_logo

经过近5个小时的迁移，终于完成了新服务器的更换了。

读者们现在所浏览的科学空间，以及大多数宇宙驿站的网站，都位于新服务器上了。这一次升级是宇宙驿站建立以来第八次升级（这个数字包含了网络升级及硬件升级），也是科学空间建立以来宇宙驿站进行的第二次升级，衷心祝福新的驿站服务器！

点击阅读全文...

原文链接：http://www.eso.org/public/news/eso1030/

译文来自：http://www.astronomy.com.cn/bbs/thread-141201-1-1.html

Stars Just Got Bigger 超大质量的巨星 A 300 Solar Mass Star Uncovered 发现超过300太阳质量的蓝超巨星

Using a combination of instruments on ESO’s Very Large Telescope, astronomers have discovered the most massive stars to date, one weighing at birth more than 300 times the mass of the Sun, or twice as much as the currently accepted limit of 150 solar masses. The existence of these monsters — millions of times more luminous than the Sun, losing weight through very powerful winds — may provide an answer to the question “how massive can stars be?”

借助于ESO的甚大望远镜（VLT），天文学家发现了创质量纪录的巨星——达300个太阳质量以上，是我们此前公认的（星族II）恒星质量上限——150个太阳的2倍。发现如此怪兽级恒星：光度是太阳的数百万倍，以极速恒星风迅速损失质量——由此产生了一个问题：恒星质量上限到底是多少？

点击阅读全文...

一张很棒的T恤印花，在心形中融汇了数学各个分支领域中最迷人的结论。
考考大家，能从中认出多少个数学研究问题或结论？

I_Heart_MathhecDetail

点击阅读全文...

量子力学中有一个很诡异的函数——Dirac函数，它似乎在物理的不少领域都有很大作用，它也具有明显的物理意义，但认真地看它却又感觉它根本就不是函数！这个“似而非是”的东西究竟是什么呢？让我们从一个物理问题引入：

设想一条质量为1，长度为$2l$的均匀直线，很显然直线的密度为$\rho=\frac{1}{2l}$；将直线的中点放置于坐标轴的原点，我们就有
$$\rho(x)=\left\{ \begin{array}{c}\frac{1}{2l} (-l \leq x \leq l)\\0 (x < -l , x > l)\end{array}\right.$$

所以有
$$\int_{-\infty}^{+\infty} \rho(x)dx=1$$

点击阅读全文...