科学空间|Scientific Spaces

我小时候一直有个疑问：

直升机上的螺旋桨能不能用来挡雨？

一般的螺旋桨是若干个“条状”物通过旋转对称而形成的，也就是说，它并非一个面，按常理来说，它是没办法用来挡雨的。但是，如果在高速旋转的情况下，甚至假设旋转速度可以任意大，那么我们任意时刻都没有办法穿过它了，这种情况下，它似乎与一个实在的面无异？

力的无穷分解

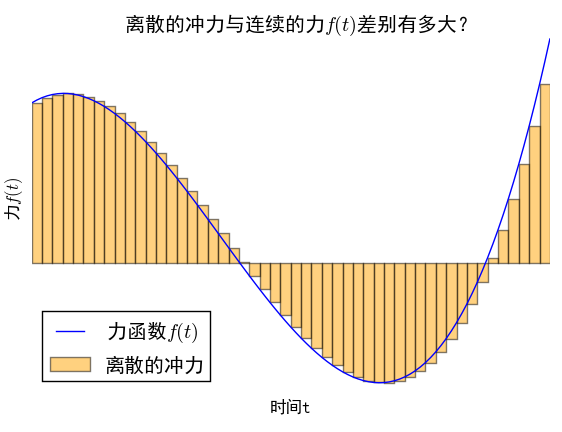
当然，以上只是笔者小时候的一个“异想天开”的念头，读者不必较真。不过，这个疑问跟本文有什么联系呢？我们在研究振动问题之时，通常会遇到在变力的作用下的受迫振动问题，已知变力是时间的函数，比如$f(t)$，然而，虽然知道$f(t)$的具体形式，但是由于$f$的非线性性，加上外力之后的运动，不一定容易求解。然而，如果可以将一个变化的力分段为无数个无穷小时间内的恒力（冲力），那么我们就可以分段讨论我们要研究的运动，而通常来说，恒力的问题会比变力容易。将一个变力离散化，然后再取极限，那么是不是跟原来在变力下的运动是一样的呢？这跟文章开头的疑问有着类似的思想——离线的极限，跟连续本身，是不是等价的？

而让人惊喜的是，在通常的物理系统中，将力分段为无数个小区间内的恒力的做法，能够导致正确的答案，而且，这恰好是线性常微分方程的格林函数法。下面我们来分析这一做法。

点击阅读全文...

在数学分析的级数理论中，有一类常见的题目，其中涉及到
$$\cos\theta+\cos 2\theta+\dots+\cos n\theta\tag{1}$$
和
$$\sin\theta+\sin 2\theta+\dots+\sin n\theta\tag{2}$$
之类的正弦或者余弦级数的求和，主要是证明该和式有界。而为了证明这一点，通常是把和式的通项求出来。当然，该级数在物理中也有重要作用，它表示$n$个相同振子的合振幅。在我们的数学分析教材中，通常是将级数乘上一项$\sin\frac{\theta}{2}$，然后利用积化和差公式完成。诚然，如果仅限在实数范围内考虑，这有可能是唯一的推导技巧的。但是这样推导的运算过程本身不简单，而且也不利于记忆，在大二的时候我就为此感到很痛苦。前几天在看费曼的书的时候，想到了一种利用复数的推导技巧。很奇怪，这个技巧是如此简单——写出来显得这篇文章都有点水了——可是我以前居然一直没留意到！看来功力尚浅，需多多修炼呀。

点击阅读全文...

昨晚上初等数论的时候，有这么一道题

求证
$$\frac{1}{3}x^3+\frac{1}{5}x^5+\frac{7}{15}x$$
恒为整数，其中$x$是一个整数。

更一般地，可以得到
$$\sum_{p\in\mathbb{P}}\frac{1}{p}x^p + \left(1-\sum_{p\in\mathbb{P}}\frac{1}{p}\right)x$$
恒为整数，其中$\mathbb{P}$是有限个素数的集合，还有更多整数值函数问题。要证明这些函数的值恒为整数，可以通过同余分析，证明分子总能被分母整除。但是，更妙的、同时往往会更简单的方法是，将结果赋予必然为整数的意义——可以是计算上的，也可以是操作上的。

点击阅读全文...

伽马函数
$$\Gamma(x)=\int_0^{+\infty}t^{x-1}e^{-t}dt$$
作为阶乘的推广，会让很多初学者感到困惑，对于笔者来说也不例外。一个最自然的问题就是：这般复杂的推广公式是如何得到的？

在cos.name的文章《神奇的伽马函数》中，有比较详细地对伽马函数的历史介绍，笔者细读之后也获益匪浅。但美中不足的是，笔者还是没能从中找到引出伽马函数的一种“自然”的办法。所谓“自然”，并不是说最简单的，而是根据一些基本的性质和定义，直接把伽马函数的表达式反解出来。它的过程和运算也许并不简单，但是思想应当是直接而简洁的。当然，我们不能苛求历史上伽马函数以这种方式诞生，但是作为事后探索是有益的，有助于我们了解伽马函数的特性。于是笔者尝试了以下途径，得到了一些结果，可是也得到了一些困惑。

点击阅读全文...

写在前面：本文是笔者数学建模课的作业，探讨了两生物种群竞争的常微分方程组模型的解的性质，展示了微分方程定性理论的基本思想。当然，本文最重要的目的，是展示LaTeX与Python的完美结合。（本文的图均由Python的Matplotlib模块生成；而文档则采用LaTeX编辑。）

问题提出

研究在同一个自然环境中生存的两个种群之间的竞争关系。假设两个种群独自在这个自然环境中生存时数量演变都服从Logistic规律，又假设当它们相互竞争时都会减慢对方数量的增长，增长速度的减小都与它们数量的乘积成正比。按照这样的假设建立的常微分方程模型为
$$\begin{equation}\label{eq:jingzhengfangcheng}\left\{\begin{aligned}\frac{dx_1}{dt}=r_1 x_1\left(1-\frac{x_1}{N_1}\right)-a_1 x_1 x_2 \\
\frac{dx_2}{dt}=r_2 x_2\left(1-\frac{x_2}{N_2}\right)-a_2 x_1 x_2\end{aligned}\right.\end{equation}$$
本文分别通过定量和定性两个角度来分析该方程的性质。

点击阅读全文...

前言：一年前国赛的时候，很初级地做了一下B题，做完之后还写了个《碎纸复原：一个人的数学建模》。当时就是对题目很有兴趣，然后通过一天的学习，基本完成了附件一二的代码，对附件三也只是有个概念。而今年我们上的数学建模课，老师把这道题作为大作业让我们做，于是我便再拾起了一年前的那份激情，继续那未完成的一个人的数学建模...

与去年不同的是，这次将所有代码用Python实现了，更简洁，更清晰，甚至可能更高效~~以下是论文全文。

研究背景

2011年10月29日，美国国防部高级研究计划局（DARPA）宣布了一场碎纸复原挑战赛（Shredder Challenge），旨在寻找到高效有效的算法，对碎纸机处理后的碎纸屑进行复原。[1]该竞赛吸引了全美9000支参赛队伍参与角逐，经过一个多月的时间，有一支队伍成功完成了官方的题目。

近年来，碎纸复原技术日益受到重视，它显示了在碎片中“还原真相”的可能性，表明我们可以从一些破碎的片段中“解密”出原始信息来。另一方面，该技术也和照片处理领域中的“全景图拼接技术”有一定联系，该技术是指通过若干张不同侧面的照片，合成一张完整的全景图。因此，分析研究碎纸复原技术，有着重要的意义。

点击阅读全文...

在高等代数的多项式一章中，通常会有这样的一道练习题：

证明任意有理数域上的多项式都能够表示为两个有理数域上的不可约多项式之和。

这是道简单的练习题，证明方法有多种。首先来介绍一个巧妙的证法。

一个巧妙证明

有理数域上的多项式问题等价于整数域上的多项式问题，因此，只需要对整数域上的多项式进行证明（这步转换使得我们可以使用艾森斯坦判别法）。设$f(x)$是整数域上的一个$n$次多项式：
$$f(x)=a_n x^n+a_{n-1} x^{n-1}+\dots+a_1 x+a_0$$
我们只需要注意到
$$p f(x)=\left[p f(x)+x^n+p\right]-(x^{n}+p)$$

点击阅读全文...

今天早上同学问了我有关伽马函数和$n$维空间的球体积之间的关系，我记得我以前想要研究，但是并没有落实。既然她提问了，那么就完成这未完成的计划吧。

标准思路

简单来说，$n$维球体积就是如下$n$重积分
$$V_n(r)=\int_{x_1^2+x_2^2+\dots+x_n^2\leq r^2}dx_1 dx_2\dots dx_n$$
用更加几何的思路，我们通过一组平行面（$n-1$维的平行面）分割，使得$n$维球分解为一系列近似小柱体，因此，可以得到递推公式
$$V_n (r)=\int_{-r}^r V_{n-1} \left(\sqrt{r^2-t^2}\right)dt$$
设$t=r\sin\theta_1$，就有
$$V_n (r)=r\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} V_{n-1} \left(r\cos\theta_1\right)\cos\theta_1 d\theta_1$$

点击阅读全文...