更便捷的Cool Papers打开方式:Chrome重定向扩展
By 苏剑林 | 2024-02-02 | 56651位读者 | 引用一些铺垫
自Cool Papers上线以来,很多用户就建议笔者加入搜索功能,后面也确实在前端用JS简单做了个页面内搜索,解决了部分用户的需求,但仍有读者希望引入更完整的全局搜索。诚然,笔者理解这个需求确实是存在,但Cool Papers的数据是逐天累积的,目前才上线一个月,论文数并不多,建立一个大而全的搜索引擎意义不大,其次做搜索也不是笔者的强项,以及并没有很好的利用LLM优化搜索的思路,等等。总而言之,暂时没有条件实现一个全面而又有特色的搜索,所以不如不做(也欢迎大家在评论区集思广益)。
后来,经过和同事讨论,想出了一个“借花献佛”的思路——写一个Chrome的重定向扩展,可以从任意页面重定向到Cool Papers。这样我们可以用任意方式(如Google搜索或者直接Arxiv官方搜索)找到Arxiv上的论文,然后右击一下就转到Cool Papers了。前两周这个扩展已经在Chrome应用商店上线,上周服务器配合做了一些调整,如今大家可以尝试使用了。
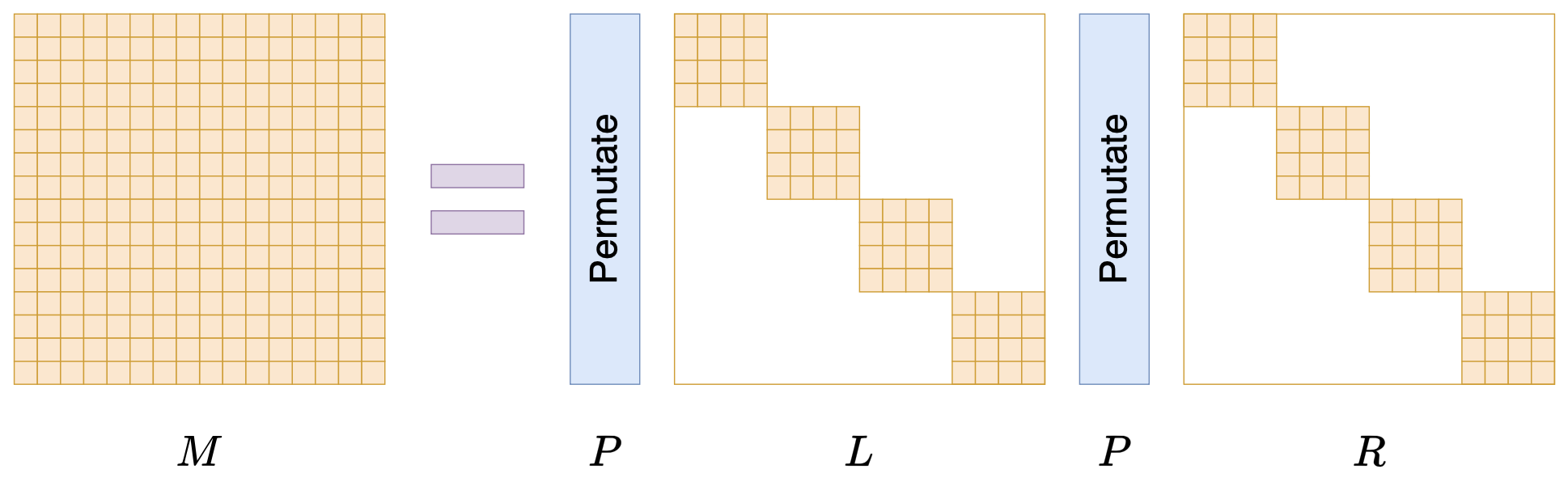
Monarch矩阵:计算高效的稀疏型矩阵分解
By 苏剑林 | 2024-07-24 | 32635位读者 | 引用在矩阵压缩这个问题上,我们通常有两个策略可以选择,分别是低秩化和稀疏化。低秩化通过寻找矩阵的低秩近似来减少矩阵尺寸,而稀疏化则是通过减少矩阵中的非零元素来降低矩阵的复杂性。如果说SVD是奔着矩阵的低秩近似去的,那么相应地寻找矩阵稀疏近似的算法又是什么呢?
接下来我们要学习的是论文《Monarch: Expressive Structured Matrices for Efficient and Accurate Training》,它为上述问题给出了一个答案——“Monarch矩阵”,这是一簇能够分解为若干置换矩阵与稀疏矩阵乘积的矩阵,同时具备计算高效且表达能力强的特点,论文还讨论了如何求一般矩阵的Monarch近似,以及利用Monarch矩阵参数化LLM来提高LLM速度等内容。
值得指出的是,该论文的作者也正是著名的Flash Attention的作者Tri Dao,其工作几乎都在致力于改进LLM的性能,这篇Monarch也是他主页上特意展示的几篇论文之一,单从这一点看就非常值得学习一番。
低秩近似之路(二):SVD
By 苏剑林 | 2024-10-01 | 23258位读者 | 引用上一篇文章中我们介绍了“伪逆”,它关系到给定矩阵\boldsymbol{M}和\boldsymbol{A}(或\boldsymbol{B})时优化目标\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2的最优解。这篇文章我们来关注\boldsymbol{A},\boldsymbol{B}都不给出时的最优解,即
\begin{equation}\mathop{\text{argmin}}_{\boldsymbol{A},\boldsymbol{B}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2\label{eq:loss-ab}\end{equation}
其中\boldsymbol{A}\in\mathbb{R}^{n\times r}, \boldsymbol{B}\in\mathbb{R}^{r\times m}, \boldsymbol{M}\in\mathbb{R}^{n\times m},r < \min(n,m)。说白了,这就是要寻找矩阵\boldsymbol{M}的“最优r秩近似(秩不超过r的最优近似)”。而要解决这个问题,就需要请出大名鼎鼎的“SVD(奇异值分解)”了。虽然本系列把伪逆作为开篇,但它的“名声”远不如SVD,听过甚至用过SVD但没听说过伪逆的应该大有人在,包括笔者也是先了解SVD后才看到伪逆。
接下来,我们将围绕着矩阵的最优低秩近似来展开介绍SVD。
结论初探
对于任意矩阵\boldsymbol{M}\in\mathbb{R}^{n\times m},都可以找到如下形式的奇异值分解(SVD,Singular Value Decomposition):
\begin{equation}\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\end{equation}
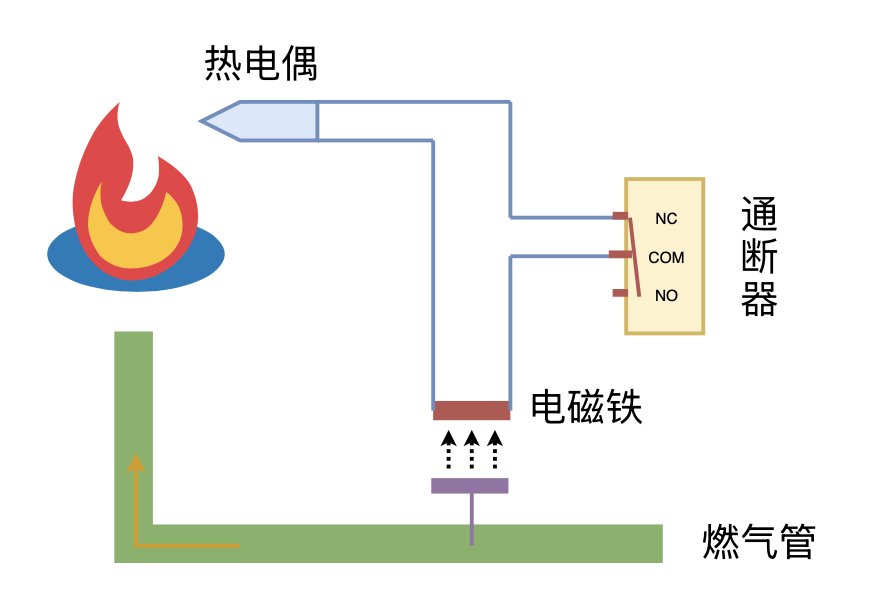
利用“熄火保护 + 通断器”实现燃气灶智能关火
By 苏剑林 | 2024-09-26 | 20319位读者 | 引用从Hessian近似看自适应学习率优化器
By 苏剑林 | 2024-11-29 | 22459位读者 | 引用这几天在重温去年的Meta的一篇论文《A Theory on Adam Instability in Large-Scale Machine Learning》,里边给出了看待Adam等自适应学习率优化器的新视角:它指出梯度平方的滑动平均某种程度上近似于在估计Hessian矩阵的平方,从而Adam、RMSprop等优化器实际上近似于二阶的Newton法。
这个角度颇为新颖,而且表面上跟以往的一些Hessian近似有明显的差异,因此值得我们去学习和思考一番。
牛顿下降
设损失函数为\mathcal{L}(\boldsymbol{\theta}),其中待优化参数为\boldsymbol{\theta},我们的优化目标是
\begin{equation}\boldsymbol{\theta}^* = \mathop{\text{argmin}}_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})\label{eq:loss}\end{equation}
假设\boldsymbol{\theta}的当前值是\boldsymbol{\theta}_t,Newton法通过将损失函数展开到二阶来寻求\boldsymbol{\theta}_{t+1}:
\begin{equation}\mathcal{L}(\boldsymbol{\theta})\approx \mathcal{L}(\boldsymbol{\theta}_t) + \boldsymbol{g}_t^{\top}(\boldsymbol{\theta} - \boldsymbol{\theta}_t) + \frac{1}{2}(\boldsymbol{\theta} - \boldsymbol{\theta}_t)^{\top}\boldsymbol{\mathcal{H}}_t(\boldsymbol{\theta} - \boldsymbol{\theta}_t)\end{equation}
矩阵的有效秩(Effective Rank)
By 苏剑林 | 2025-04-10 | 4365位读者 | 引用秩(Rank)是线性代数中的重要概念,它代表了矩阵的内在维度。然而,数学上对秩的严格定义,很多时候并不完全适用于数值计算场景,因为秩等于非零奇异值的个数,而数学上对“等于零”这件事的理解跟数值计算有所不同,数学上的“等于零”是绝对地、严格地等于零,哪怕是10^{-100}也是不等于零,但数值计算不一样,很多时候10^{-10}就可以当零看待。
因此,我们希望将秩的概念推广到更符合数值计算特性的形式,这便是有效秩(Effective Rank)概念的由来。
误差截断
需要指出的是,目前学术界对有效秩并没有统一的定义,接下来我们介绍的是一些从不同角度切入来定义有效秩的思路。对于实际问题,读者可以自行选择适合的定义来使用。
通过梯度近似寻找Normalization的替代品
By 苏剑林 | 2025-04-02 | 6902位读者 | 引用不知道大家有没有留意到前段时间的《Transformers without Normalization》?这篇论文试图将Transformer模型中的Normalization层用一个Element-wise的运算DyT替代,以期能提高速度并保持效果。这种基础架构的主题本身自带一点吸引力,加之Kaiming He和Yann LeCun两位大佬挂名,所以这篇论文发布之时就引起了不少围观,评价也是有褒有贬。
无独有偶,上周的一篇新论文《The Mathematical Relationship Between Layer Normalization and Dynamic Activation Functions》从梯度分析和微分方程的视角解读了DyT,并提出了新的替代品。个人感觉这个理解角度非常本质,遂学习和分享一波。
写在前面
DyT全称是Dynamic Tanh,它通过如下运算来替代Normalization层:
\begin{equation}\mathop{\text{DyT}}(\boldsymbol{x}) = \boldsymbol{\gamma} \odot \tanh(\alpha \boldsymbol{x}) + \boldsymbol{\beta}\end{equation}
在生活上,我是一个比较传统的人,因此每到节日我都会尽量回家跟家人团聚。也许会让大家比较吃惊的是,今年的国庆是我第一个不在家的国庆。的确,从小学到高中,上学的地方离家都比较近,每周回去一次都是不成问题的。现在来到了广州,就不能太随心了。虽然跟很多同学相比,我离家还是比较近的,但是来回也要考虑车费、时间等等。国庆假期时间虽然很长,但是中秋已经回去一趟了,所以我决定国庆就不再回去了。
对我来说,中秋跟国庆相比,中秋的意义更大些。所以我选择了国庆不回家。对家人而言,看到自己平安就好,因此哪一天回去他们都会很高兴,当然,对于农村人来说,中秋的味道更浓,更希望团聚。








最近评论