生成扩散模型漫谈(十五):构建ODE的一般步骤(中)
By 苏剑林 | 2022-12-22 | 36261位读者 | 引用上周笔者写了《生成扩散模型漫谈(十四):构建ODE的一般步骤(上)》(当时还没有“上”这个后缀),本以为已经窥见了构建ODE扩散模型的一般规律,结果不久后评论区大神 @gaohuazuo 就给出了一个构建格林函数更高效、更直观的方案,让笔者自愧不如。再联想起之前大神之前在《生成扩散模型漫谈(十二):“硬刚”扩散ODE》同样也给出了一个关于扩散ODE的精彩描述(间接启发了上一篇博客的结果),大神的洞察力不得不让人叹服。
经过讨论和思考,笔者发现大神的思路本质上就是一阶偏微分方程的特征线法,通过构造特定的向量场保证初值条件,然后通过求解微分方程保证终值条件,同时保证了初值和终值条件,真的非常巧妙!最后,笔者将自己的收获总结成此文,作为上一篇的后续。
前情回顾
简单回顾一下上一篇文章的结果。假设随机变量\boldsymbol{x}_0\in\mathbb{R}^d连续地变换成\boldsymbol{x}_T,其变化规律服从ODE
\begin{equation}\frac{d\boldsymbol{x}_t}{dt}=\boldsymbol{f}_t(\boldsymbol{x}_t)\label{eq-ode}\end{equation}
用热传导方程来指导自监督学习
By 苏剑林 | 2022-11-30 | 34881位读者 | 引用用理论物理来卷机器学习已经不是什么新鲜事了,比如上个月介绍的《生成扩散模型漫谈(十三):从万有引力到扩散模型》就是经典一例。最近一篇新出的论文《Self-Supervised Learning based on Heat Equation》,顾名思义,用热传导方程来做(图像领域的)自监督学习,引起了笔者的兴趣。这种物理方程如何在机器学习中发挥作用?同样的思路能否迁移到NLP中?让我们一起来读读论文。
基本方程
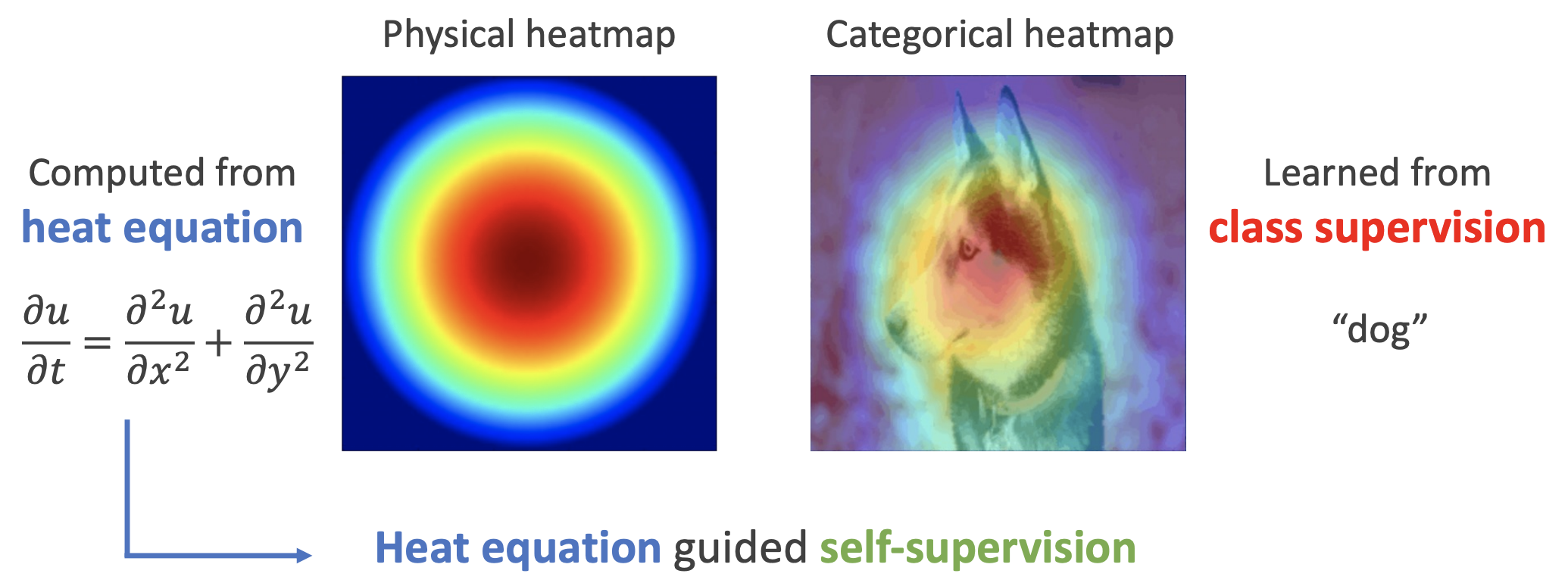
如下图,左边是物理中热传导方程的解,右端则是CAM、积分梯度等显著性方法得到的归因热力图,可以看到两者有一定的相似之处,于是作者认为热传导方程可以作为好的视觉特征的一个重要先验。
生成扩散模型漫谈(十四):构建ODE的一般步骤(上)
By 苏剑林 | 2022-12-15 | 66939位读者 | 引用书接上文,在《生成扩散模型漫谈(十三):从万有引力到扩散模型》中,我们介绍了一个由万有引力启发的、几何意义非常清晰的ODE式生成扩散模型。有的读者看了之后就疑问:似乎“万有引力”并不是唯一的选择,其他形式的力是否可以由同样的物理绘景构建扩散模型?另一方面,该模型在物理上确实很直观,但还欠缺从数学上证明最后确实能学习到数据分布。
本文就尝试从数学角度比较精确地回答“什么样的力场适合构建ODE式生成扩散模型”这个问题。
基础结论
要回答这个问题,需要用到在《生成扩散模型漫谈(十二):“硬刚”扩散ODE》中我们推导过的一个关于常微分方程对应的分布变化的结论。
考虑\boldsymbol{x}_t\in\mathbb{R}^d, t\in[0,T]的一阶(常)微分方程(组)
\begin{equation}\frac{d\boldsymbol{x}_t}{dt}=\boldsymbol{f}_t(\boldsymbol{x}_t)\label{eq:ode}\end{equation}
Transformer升级之路:6、旋转位置编码的完备性分析
By 苏剑林 | 2022-12-28 | 46202位读者 | 引用在去年的文章《Transformer升级之路:2、博采众长的旋转式位置编码》中,笔者提出了旋转位置编码(RoPE),当时的出发点只是觉得用绝对位置来实现相对位置是一件“很好玩的事情”,并没料到其实际效果还相当不错,并为大家所接受,不得不说这真是一个意外之喜。后来,在《Transformer升级之路:4、二维位置的旋转式位置编码》中,笔者讨论了二维形式的RoPE,并研究了用矩阵指数表示的RoPE的一般解。
既然有了一般解,那么自然就会引出一个问题:我们常用的RoPE,只是一个以二维旋转矩阵为基本单元的分块对角矩阵,如果换成一般解,理论上效果会不会更好呢?本文就来回答这个问题。
指数通解
在《Transformer升级之路:4、二维位置的旋转式位置编码》中,我们将RoPE抽象地定义为任意满足下式的方阵
\begin{equation}\boldsymbol{\mathcal{R}}_m^{\top}\boldsymbol{\mathcal{R}}_n=\boldsymbol{\mathcal{R}}_{n-m}\label{eq:re}\end{equation}
智能家居之热水器零冷水技术原理浅析
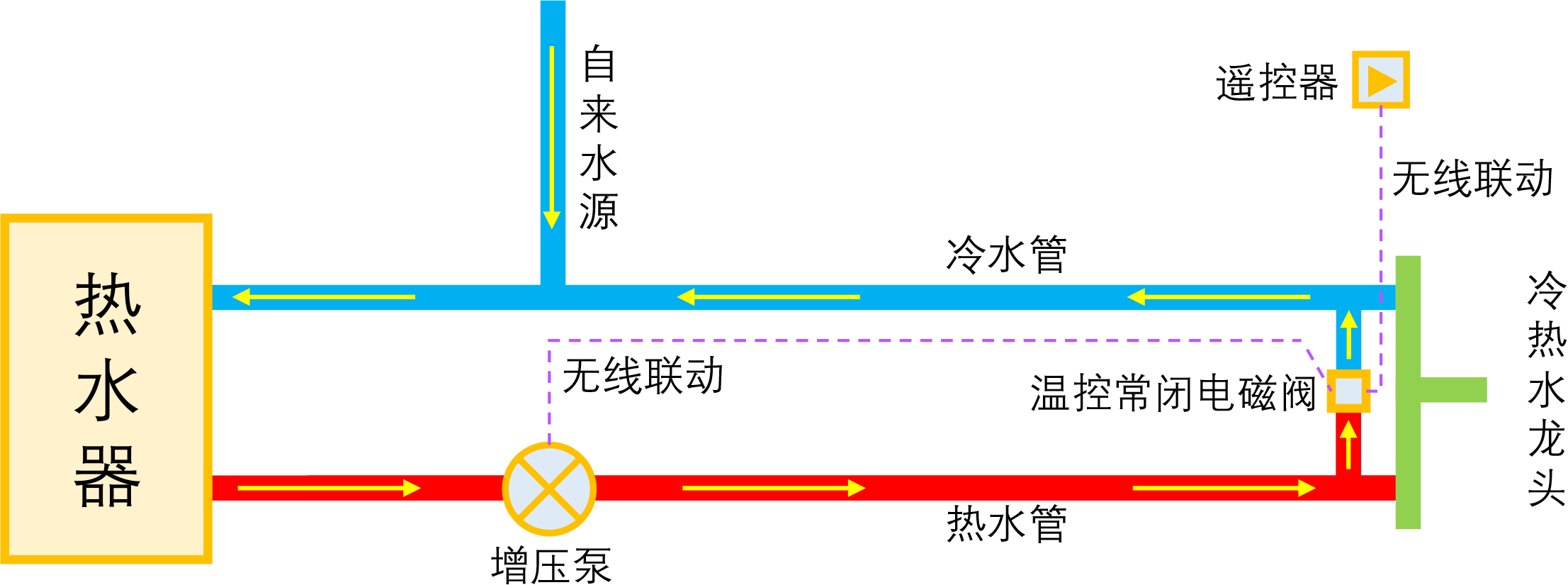
By 苏剑林 | 2023-01-04 | 53942位读者 | 引用如果家庭使用单一的热水器集中供热水,那么当我们想要用热水时,往往需要先放一段时间的冷水,而如果放冷水时间比较长的话,就会比较影响体验。所谓零冷水,实际上就是想办法提前把热水管中的冷水排放掉,以达到(几乎)瞬间出热水的效果。事实上,零冷水并不是什么高大上的技术,但可能由于观念没跟上、理解上有误等原因,零冷水技术还没有在家庭中得到普及,不过随着大家对生活品质的要求越来越高,零冷水确实在慢慢流行起来了。
本文来简单分析一下零冷水技术的实现原理,包括各种方案的优缺点和自省DIY的参考思路。
写在前面
在文章开始,需要纠正很多人的一个错误观念:零冷水不是为了省钱,而是为了提升生活品质。如果你是省钱最大的心态,那么接下来的内容就可以不用看了,零冷水技术对你毫无价值。
注意力和Softmax的两点有趣发现:鲁棒性和信息量
By 苏剑林 | 2023-04-25 | 35293位读者 | 引用最近几周笔者一直都在思考注意力机制的相关性质,在这个过程中对注意力及Softmax有了更深刻的理解。在这篇文章中,笔者简单分享其中的两点:
1、Softmax注意力天然能够抵御一定的噪声扰动;
2、从信息熵角度也可以对初始化问题形成直观理解。
鲁棒性
基于Softmax归一化的注意力机制,可以写为
\begin{equation}o = \frac{\sum\limits_{i=1}^n e^{s_i} v_i}{\sum\limits_{i=1}^n e^{s_i}}\end{equation}
有一天笔者突然想到一个问题:如果往s_i中加入独立同分布的噪声会怎样?
梯度视角下的LoRA:简介、分析、猜测及推广
By 苏剑林 | 2023-04-17 | 86405位读者 | 引用随着ChatGPT及其平替的火热,各种参数高效(Parameter-Efficient)的微调方法也“水涨船高”,其中最流行的方案之一就是本文的主角LoRA了,它出自论文《LoRA: Low-Rank Adaptation of Large Language Models》。LoRA方法上比较简单直接,而且也有不少现成实现,不管是理解还是使用都很容易上手,所以本身也没太多值得细写的地方了。
然而,直接实现LoRA需要修改网络结构,这略微麻烦了些,同时LoRA给笔者的感觉是很像之前的优化器AdaFactor,所以笔者的问题是:能否从优化器角度来分析和实现LoRA呢?本文就围绕此主题展开讨论。
方法简介
以往的一些结果(比如《Exploring Aniversal Intrinsic Task Subspace via Prompt Tuning》)显示,尽管预训练模型的参数量很大,但每个下游任务对应的本征维度(Intrinsic Dimension)并不大,换句话说,理论上我们可以微调非常小的参数量,就能在下游任务取得不错的效果。
LoRA借鉴了上述结果,提出对于预训练的参数矩阵W_0\in\mathbb{R}^{n\times m},我们不去直接微调W_0,而是对增量做低秩分解假设:
\begin{equation}W = W_0 + A B,\qquad A\in\mathbb{R}^{n\times r},B\in\mathbb{R}^{r\times m}\end{equation}
Google新搜出的优化器Lion:效率与效果兼得的“训练狮”
By 苏剑林 | 2023-02-16 | 58120位读者 | 引用昨天在Arixv上发现了Google新发的一篇论文《Symbolic Discovery of Optimization Algorithms》,主要是讲自动搜索优化器的,咋看上去没啥意思,因为类似的工作也有不少,大多数结果都索然无味。然而,细读之下才发现别有洞天,原来作者们通过数千TPU小时的算力搜索并结合人工干预,得到了一个速度更快、显存更省的优化器Lion(EvoLved Sign Momentum,不得不吐槽这名字起得真勉强),并在图像分类、图文匹配、扩散模型、语言模型预训练和微调等诸多任务上做了充分的实验,多数任务都显示Lion比目前主流的AdamW等优化器有着更好的效果。
更省显存还更好效果,真可谓是鱼与熊掌都兼得了,什么样的优化器能有这么强悍的性能?本文一起来欣赏一下论文的成果。
先说结果
本文主要关心搜索出来的优化器本身,所以关于搜索过程的细节就不讨论了,对此有兴趣读者自行看原论文就好。Lion优化器的更新过程为
\begin{equation}\text{Lion}:=\left\{\begin{aligned}
&\boldsymbol{u}_t = \text{sign}\big(\beta_1 \boldsymbol{m}_{t-1} + \left(1 - \beta_1\right) \boldsymbol{g}_t\big) \\
&\boldsymbol{\theta}_t = \boldsymbol{\theta}_{t-1} - \eta_t (\boldsymbol{u}_t \color{skyblue}{ + \lambda_t \boldsymbol{\theta}_{t-1}}) \\
&\boldsymbol{m}_t = \beta_2 \boldsymbol{m}_{t-1} + \left(1 - \beta_2\right) \boldsymbol{g}_t
\end{aligned}\right.\end{equation}








最近评论