科学空间|Scientific Spaces

《量子力学与路径积分》封面

今天收到高教出版社的王超编辑寄来的费曼著作新版《量子力学与路径积分》了，兴奋ing...

《量子力学与路径积分》是费曼的一本经典著作，更是量子力学的经典著作——它是我目前读过的唯一一本从路径积分出发、并且以路径积分为第一性原理的量子力学著作(徐一鸿的《简明量子场论》好象是我读过的唯一一本纯粹以路径积分为方法的量子场论著作，也非常不错)，其它类型的量子力学著作，也有部分谈到路径积分，但无一不是从哈密顿形式中引出路径积分的，在那种情况之下，路径积分只能算是一个推论。但是路径积分明明就作为量子力学的三种形式之一，它应该是可以作为量子力学的基本原理来提出的，而不应该作为另一种形式的推论。费曼做了尝试——从路径积分出发讲解量子力学，而且显然这种尝试是很成功的，至少对于我来说，路径积分是一种非常容易理解的量子力学形式。（这也许跟我的数学基础有关）

点击阅读全文...

神经网络

在所有机器学习模型之中，也许最有趣、最深刻的便是神经网络模型了。笔者也想献丑一番，说一次神经网络。当然，本文并不打算从头开始介绍神经网络，只是谈谈我对神经网络的个人理解。如果希望进一步了解神经网络与深度学习的朋友，请移步阅读下面的教程：
http://deeplearning.stanford.edu/wiki/index.php/UFLDL教程

http://blog.csdn.net/zouxy09/article/details/8775360

机器分类

这里以分类工作为例，数据挖掘或机器学习中，有很多分类的问题，比如讲一句话的情况进行分类，粗略点可以分类为“积极”或“消极”，精细点分为开心、生气、忧伤等；另外一个典型的分类问题是手写数字识别，也就是将图片分为10类（0,1,2,3,4,5,6,7,8,9）。因此，也产生了很多分类的模型。

点击阅读全文...

很多人觉得“模型”、“大数据”、“机器学习”这些字眼很高大很神秘，事实上，它跟我们生活中选水果差不了多少。本文用了几千字，来试图教会大家怎么选芒果...

模型的比喻

芒果

假如我要从一批芒果中，找出好吃的那个来。而我不能直接切开芒果尝尝，所以我只能观察芒果，能观察到的量有颜色、表面的气味、大小等等，这些就是我们能够收集到的信息（特征）。

生活中还要很多这样的例子，比如买火柴（可能年轻的城里人还没见过火柴？），如何判断一盒火柴的质量？难道要每根火柴都划划，看看着不着火？显然不行，我们最多也只能划几根，全部划了，火柴也不成火柴了。当然，我们还能看看火柴的样子，闻闻火柴的气味，这些动作是可以接受的。

点击阅读全文...

斯特灵近似，或者称斯特灵公式，最开始是作为阶乘的近似提出
$$n!\sim \sqrt{2\pi n}\left(\frac{n}{e}\right)^n$$
符号$\sim$意味着
$$\lim_{n\to\infty}\frac{\sqrt{2\pi n}\left(\frac{n}{e}\right)^n}{n!}=1$$
将斯特灵公式进一步提高精度，就得到所谓的斯特灵级数
$$n!=\sqrt{2\pi n}\left(\frac{n}{e}\right)^n\left(1+\frac{1}{12n}+\frac{1}{288n^2}\dots\right)$$
很遗憾，这个是渐近级数。

相关资料有：
https://zh.wikipedia.org/zh-cn/斯特灵公式

https://en.wikipedia.org/wiki/Stirling%27s_approximation

本文将会谈到斯特灵公式及其渐近级数的一个改进的推导，并解释渐近级数为什么渐近。

点击阅读全文...

咋看上去，SVD分解是比较传统的数据挖掘手段，自编码器是深度学习中一个比较“先进”的概念，应该没啥交集才对。而本文则要说，如果不考虑激活函数，那么两者将是等价的。进一步的思考就可以发现，不管是SVD还是自编码器，我们降维，并不是纯粹地为了减少储存量或者减少计算量，而是“智能”的初步体现。

等价性

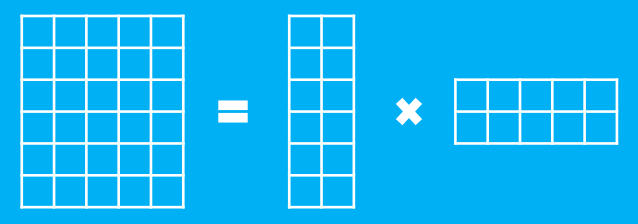
假设有一个$m$行$n$列的庞大矩阵$M_{m\times n}$，这可能使得计算甚至存储上都成问题，于是考虑一个分解，希望找到矩阵$A_{m\times k}$和$B_{k\times n}$，使得
$$M_{m\times n}=A_{m\times k}\times B_{k\times n}$$
这里的乘法是矩阵乘法。如图

SVD

点击阅读全文...

事实上，在论文《Dynamic Routing Between Capsules》发布不久后，一篇新的Capsule论文《Matrix Capsules with EM Routing》就已经匿名公开了（在ICLR 2018的匿名评审中），而如今作者已经公开，他们是Geoffrey Hinton, Sara Sabour, Nicholas Frosst。不出大家意料，作者果然有Hinton。

大家都知道，像Hinton这些“鼻祖级”的人物，发表出来的结果一般都是比较“重磅”的。那么，这篇新论文有什么特色呢？

在笔者的思考过程中，文章《Understanding Matrix capsules with EM Routing 》给了我颇多启示，知乎上各位大神的相关讨论也加速了我的阅读，在此表示感谢。

论文摘要

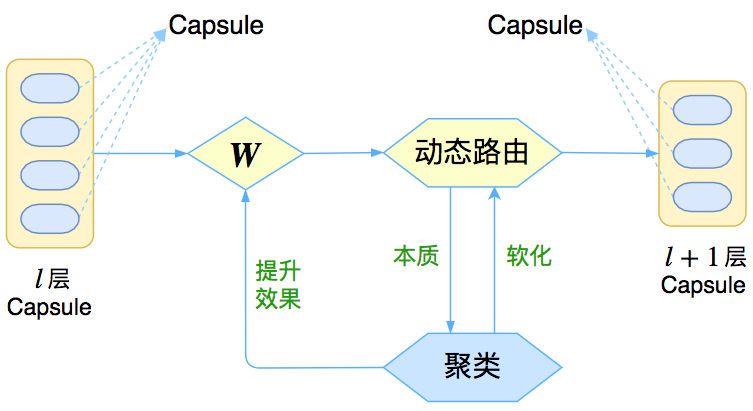
让我们先来回忆一下上一篇介绍《再来一顿贺岁宴：从K-Means到Capsule》中的那个图

Capsule框架的简明示意图

这个图表明，Capsule事实上描述了一个建模的框架，这个框架中的东西很多都是可以自定义的，最明显的是聚类算法，可以说“有多少种聚类算法就有多少种动态路由”。那么这次Hinton修改了什么呢？总的来说，这篇新论文有以下几点新东西：

1、原来用向量来表示一个Capsule，现在用矩阵来表示；

2、聚类算法换成了GMM（高斯混合模型）；

3、在实验部分，实现了Capsule版的卷积。

点击阅读全文...

Keras伴我走来

回想起进入机器学习领域的这两三年来，Keras是一直陪伴在笔者的身边。要不是当初刚掉进这个坑时碰到了Keras这个这么易用的框架，能快速实现我的想法，我也不确定我是否能有毅力坚持下来，毕竟当初是theano、pylearn、caffe、torch等的天下，哪怕在今天它们对我来说仍然像天书一般。

后来为了拓展视野，我也去学习了一段时间的tensorflow，用纯tensorflow写过若干程序，但不管怎样，仍然无法割舍Keras。随着对Keras的了解的深入，尤其是花了一点时间研究过Keras的源码后，我发现Keras并没有大家诟病的那样“欠缺灵活性”。事实上，Keras那精巧的封装，可以让我们轻松实现很多复杂的功能。我越来越感觉，Keras像是一件非常精美的艺术品，充分体现了Keras的开发者们深厚的创作功力。

本文介绍Keras中自定义模型的一些内容，相对而言，这属于Keras进阶的内容，刚入门的朋友请暂时忽略。

层的自定义

这里介绍Keras中自定义层及其一些运用技巧，在这之中我们可以看到Keras层的精巧之处。

点击阅读全文...

话在开头

上一篇文章《细水长flow之NICE：流模型的基本概念与实现》中，我们介绍了flow模型中的一个开山之作：NICE模型。从NICE模型中，我们能知道flow模型的基本概念和基本思想，最后笔者还给出了Keras中的NICE实现。

本文我们来关心NICE的升级版：RealNVP和Glow。

精巧的flow

不得不说，flow模型是一个在设计上非常精巧的模型。总的来看，flow就是想办法得到一个encoder将输入$\boldsymbol{x}$编码为隐变量$\boldsymbol{z}$，并且使得$\boldsymbol{z}$服从标准正态分布。得益于flow模型的精巧设计，这个encoder是可逆的，从而我们可以立马从encoder写出相应的decoder（生成器）出来，因此，只要encoder训练完成，我们就能同时得到decoder，完成生成模型的构建。

为了完成这个构思，不仅仅要使得模型可逆，还要使得对应的雅可比行列式容易计算，为此，NICE提出了加性耦合层，通过多个加性耦合层的堆叠，使得模型既具有强大的拟合能力，又具有单位雅可比行列式。就这样，一种不同于VAE和GAN的生成模型——flow模型就这样出来了，它通过巧妙的构造，让我们能直接去拟合概率分布本身。

点击阅读全文...