科学空间|Scientific Spaces

Efficient Transformer，泛指一切致力于降低Transformer的二次复杂度的工作，开始特指针对Attention的改进，后来更一般的思路，如傅里叶变换、线性RNN等，也被归入这个范畴。不得不说，为了降低Transformer的二次复杂度，各路大牛可谓是“八仙过海，各显神通”，各种神奇的思路“百花齐放”，笔者也从中学习到了不少理论知识。然而，尽管Efficient Transformer在理论上是精彩的，但实际上该领域一直都是不愠不火的状态，并没有实际表现十分出色的模型，在LLM火爆的今天，甚至已经逐渐淡出了大家的视野，也淡出了笔者的兴趣范围。

不过，最近有一篇论文《Transformer-VQ: Linear-Time Transformers via Vector Quantization》，却让笔者为之拍案叫绝。作者非常高明地洞察到，只需要对标准Attention的Key做一下VQ（Vector Quantize），复杂度就会自动降低为线性！这种线性化思路保留了标准Attention的形式，是标准Attention到线性Attention的一个完美过渡，同时最大程度上保留了标准Attention的能力。

高效难题

说起来，本站也算是比较早关注Efficient Transformer相关工作了，最早可以追溯到2019年解读Sparse Transformer的一篇博客《为节约而生：从标准Attention到稀疏Attention》。此后，陆续写的关于Efficient Transformer的其他博文还有

点击阅读全文...

不论是在基础的分类任务中，还是如今无处不在的注意力机制中，概率分布的构建都是一个关键步骤。具体来说，就是将一个$n$维的任意向量，转换为一个$n$元的离散型概率分布。众所周知，这个问题的标准答案是Softmax，它是指数归一化的形式，相对来说比较简单直观，同时也伴有很多优良性质，从而成为大部分场景下的“标配”。

尽管如此，Softmax在某些场景下也有一些不如人意之处，比如不够稀疏、无法绝对等于零等，因此很多替代品也应运而生。在这篇文章中，我们将简单总结一下Softmax的相关性质，并盘点和对比一下它的部分替代方案。

Softmax回顾

首先引入一些通用记号：$\boldsymbol{x} = (x_1,x_2,\cdots,x_n)\in\mathbb{R}^n$是需要转为概率分布的$n$维向量，它的分量可正可负，也没有限定的上下界。$\Delta^{n-1}$定义为全体$n$元离散概率分布的集合，即
\begin{equation}\Delta^{n-1} = \left\{\boldsymbol{p}=(p_1,p_2,\cdots,p_n)\left|\, p_1,p_2,\cdots,p_n\geq 0,\sum_{i=1}^n p_i = 1\right.\right\}\end{equation}
之所以标注$n-1$而不是$n$，是因为约束$\sum\limits_{i=1}^n p_i = 1$定义了$n$维空间中的一个$n-1$维子平面，再加上$p_i\geq 0$的约束，$(p_1,p_2,\cdots,p_n)$的集合就只是该平面的一个子集，即实际维度只有$n-1$。

点击阅读全文...

由于图像质量等原因，性能再好的识别模型，都会有识别错误的可能性，为了减少识别错误率，可以将识别问题跟统计语言模型结合起来，通过动态规划的方法给出最优的识别结果.这是改进OCR识别效果的重要方法之一.

转移概率

在我们分析实验结果的过程中，有出现这一案例.由于图像不清晰等可能的原因，导致“电视”一词被识别为“电柳”，仅用图像模型是不能很好地解决这个问题的，因为从图像模型来看，识别为“电柳”是最优的选择.但是语言模型却可以很巧妙地解决这个问题.原因很简单，基于大量的文本数据我们可以统计“电视”一词和“电柳”一词的概率，可以发现“电视”一词的概率远远大于“电柳”，因此我们会认为这个词是“电视”而不是“电柳”.

从概率的角度来看，就是对于第一个字的区域的识别结果$s_1$，我们前面的卷积神经网络给出了“电”、“宙”两个候选字(仅仅选了前两个，后面的概率太小)，每个候选字的概率$W(s_1)$分别为0.99996、0.00004；第二个字的区域的识别结果$s_2$，我们前面的卷积神经网络给出了“柳”、“视”、“规”(仅仅选了前三个，后面的概率太小)，每个候选字的概率$W(s_2)$分别为0.87838、0.12148、0.00012，因此，它们事实上有六种组合：“电柳”、“电视”、“电规”、“宙柳”、“宙视”、“宙规”.

点击阅读全文...

暑假期间做了一下百度和西安交大联合举办的核心实体识别竞赛，最终的结果还不错，遂记录一下。模型的效果不是最好的，但是胜在“端到端”，迁移性强，估计对大家会有一定的参考价值。

比赛的主题是“核心实体识别”，其实有两个任务：核心识别 + 实体识别。这两个任务虽然有关联，但在传统自然语言处理程序中，一般是将它们分开处理的，而这次需要将两个任务联合在一起。如果只看“核心识别”，那就是传统的关键词抽取任务了，不同的是，传统的纯粹基于统计的思路（如TF-IDF抽取）是行不通的，因为单句中的核心实体可能就只出现一次，这时候统计估计是不可靠的，最好能够从语义的角度来理解。我一开始就是从“核心识别”入手，使用的方法类似QA系统：

1、将句子分词，然后用Word2Vec训练词向量；

2、用卷积神经网络（在这种抽取式问题上，CNN效果往往比RNN要好）卷积一下，得到一个与词向量维度一样的输出；

3、损失函数就是输出向量跟训练样本的核心词向量的cos值。

点击阅读全文...

统计是通过大量样本来估计真实分布的过程，通常与统计相伴出现的一个词是“平滑”，即对统计结果打折扣的处理过程。平滑的思想来源于：如果样本空间非常大，那么统计的结果是稀疏的，这样由于各种偶然因素的存在，导致了小的统计结果不可靠，如频数为1的结果可能只是偶然的结果，其频率并不一定近似于$1/N$，频数为0的不一定就不会出现。这样我们就需要对统计结果进行平滑，使得结论更为可靠。

平滑的方法有很多，这里介绍一种基于遗忘假设的平滑公式。假设的任务为：我们要从一批语料中，统计每个字的字频。我们模仿人脑遗忘的过程，假设这个字出现一次，我们脑里的记忆量就增加1，但是如果一个周期内（先不管这个周期多大），这个字都没有出现，那么脑里的记忆量就变为原来的$\beta$比例。假设字是周期性出现的，那么记忆量$A_n$就满足如下递推公式
$$A_{n+1} = \beta A_n + 1$$

点击阅读全文...

咋看上去，SVD分解是比较传统的数据挖掘手段，自编码器是深度学习中一个比较“先进”的概念，应该没啥交集才对。而本文则要说，如果不考虑激活函数，那么两者将是等价的。进一步的思考就可以发现，不管是SVD还是自编码器，我们降维，并不是纯粹地为了减少储存量或者减少计算量，而是“智能”的初步体现。

等价性

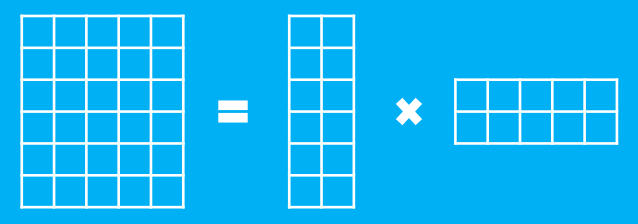
假设有一个$m$行$n$列的庞大矩阵$M_{m\times n}$，这可能使得计算甚至存储上都成问题，于是考虑一个分解，希望找到矩阵$A_{m\times k}$和$B_{k\times n}$，使得
$$M_{m\times n}=A_{m\times k}\times B_{k\times n}$$
这里的乘法是矩阵乘法。如图

SVD

点击阅读全文...

这篇文章要带来一个“重磅”消息，如标题所示，居然连大名鼎鼎的深度学习词向量工具Word2Vec都只不过是个SVD！

当然，Word2Vec的超级忠实粉丝们，你们也不用太激动，这里只是说模型结构上是等价的，并非完全等价，Word2Vec还是有它的独特之处。只不过，经过我这样解释之后，估计很多问题就可以类似想通了。

词向量=one hot

让我们先来回顾一下去年的一篇文章《词向量与Embedding究竟是怎么回事？》，这篇文章主要说的是：所谓Embedding层，就是一个one hot的全连接层罢了（再次强调，这里说的完全等价，而不是“相当于”），而词向量，就是这个全连接层的参数；至于Word2Vec，就通过大大简化的语言模型来训练Embedding层，从而得到词向量（它的优化技巧有很多，但模型结构就只是这么简单）；词向量能够减少过拟合风险，是因为用Word2Vec之类的工具、通过大规模语料来无监督地预训练了这个Embedding层，而跟one hot还是Embedding还是词向量本身没啥关系。

有了这个观点后，马上可以解释我们以前的一个做法为什么可行了。在做情感分类问题时，如果有了词向量，想要得到句向量，最简单的一个方案就是直接对句子中的词语的词向量求和或者求平均，这约能达到85%的准确率。事实上这也是facebook出品的文本分类工具FastText的做法了（FastText还多引入了ngram特征，来缓解词序问题，但总的来说，依旧是把特征向量求平均来得到句向量）。为什么这么一个看上去毫不直观的、简单粗暴的方案也能达到这么不错的准确率？

点击阅读全文...

PS：本文就是梳理了梯度下降与EM算法的关系，通过同一种思路，推导了普通的梯度下降法、pLSA中的EM算法、K-Means中的EM算法，以此表明它们基本都是同一个东西的不同方面，所谓“横看成岭侧成峰，远近高低各不同”罢了。

在机器学习中，通常都会将我们所要求解的问题表示为一个带有未知参数的损失函数(Loss)，如平均平方误差（MSE），然后想办法求解这个函数的最小值，来得到最佳的参数值，从而完成建模。因将函数乘以-1后，最大值也就变成了最小值，因此一律归为最小值来说。如何求函数的最小值，在机器学习领域里，一般会流传两个大的方向：1、梯度下降；2、EM算法，也就是最大期望算法，一般用于复杂的最大似然问题的求解。

在通常的教程中，会将这两个方法描述得迥然不同，就像两大体系在分庭抗礼那样，而EM算法更是被描述得玄乎其玄的感觉。但事实上，这两个方法，都是同一个思路的不同例子而已，所谓“本是同根生”，它们就是一脉相承的东西。

让我们，先从远古的牛顿法谈起。

牛顿迭代法

给定一个复杂的非线性函数$f(x)$，希望求它的最小值，我们一般可以这样做，假定它足够光滑，那么它的最小值也就是它的极小值点，满足$f'(x_0)=0$，然后可以转化为求方程$f'(x)=0$的根了。非线性方程的根我们有个牛顿法，所以
\begin{equation}x_{n+1} = x_{n} - \frac{f'(x_n)}{f''(x_n)}\end{equation}

点击阅读全文...