科学空间|Scientific Spaces

据美国宇航局太空网报道，人类首次登陆月球40周年庆典已经结束，但是美国宇航局能否把人类送上火星仍是一个谜。

休斯顿美国宇航局约翰逊太空中心月球和火星综合研究部研究人员布雷特·德雷克(Bret Drake)说：“目前我们仍把人类探索火星看成是未来的最高目标。人类踏上另一颗行星的风险可能最大，但它也是最有历史纪念意义的事情。”

当前的科技水平可能刚刚达到，也有可能还远远不及前往火星的载人任务所需的技术水平。因此前往这颗红色行星的载人任务仍是一个巨大挑战。但是美国宇航局仍坚持远征火星，而且有关火星探索的新想法层出不穷。德雷克说：“火星是长期以来我们一直向往的地方。”

点击阅读全文...

图片说明：超新星遗骸E0102-72，版权:X-ray - NASA / CXC / MIT / D.Dewey et al., NASA / CXC / SAO / J.DePasquale; Optical - NASA / STScI

点击阅读全文...

“引力走廊”能够帮助飞船在太阳系内穿行，就像船只利用洋流航行一样。

新浪科技讯 北京时间9月11日消息，据英国《每日邮报》报道，美国科学家10日表示，“引力走廊”能够帮助飞船在太阳系内穿行，就像船只利用洋流航行一样。目前，美国科学家正试图对图片中蜿蜒曲折的管道进行测绘，这些管道能够减少太空飞行的成本。

点击阅读全文...

How time flies!
时间飞逝！

开学的日子仿佛在昨天，2009年似乎几个小时前才过，而今天又再次到了寒假。
这是我的高中的第一个寒假，也是一个Unusual Long Holidays！（不同往常的长假）

往年，除了老师强加给我们的寒假作业外，我从来不会自觉学些什么。就算真的收获了些什么，也是意外的收获。因为我认为，假期就是用来放松的。

点击阅读全文...

法新社报道说，一名不愿意透露姓名的白宫顾问说，“（重返月球的）星座计划已经死亡。”

新一代探月飞行器假想图

28日，美国官员透露，布什政府于2004年通过的、计划耗资高达2300亿美元的“重返月球”计划实际上已经被美国总统奥巴马搁浅了。相反，奥巴马在未来五年将向美国国家航空航天局（NASA）拨款59亿美元，其中一部分将用于延长国际太空站的使用寿命至2020年，另外还将用于在航天飞机退役后，鼓励私人公司研制航天器来向空间站运送宇航员。随着“重返月球”计划的终结，新一代“土星”系列火箭、登月飞船、月球车等一系列相关设备的研制计划也将终止，可以在很大程度上减轻美国政府的财政压力。

点击阅读全文...

自由落体公式-示意图

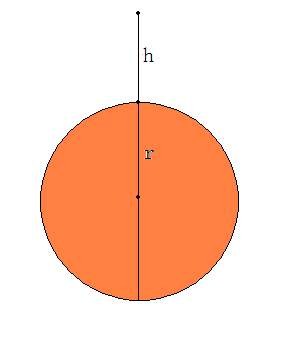
自由落体的一般定义是：只考虑吸引天体和被吸引天体的引力因素，忽略其他的运动和大气摩擦等因素，物体从静止（相对于吸引天体）开始接近吸引天体的运动。根据这个定义，假设地球为一个均匀球体，半径为r，质量为M，物体从距离地表h高度处自由落下。求落到地面的时间t，或者根据时间t求h。

令s为t时刻物体左右下落的物体与地表的距离，忽略物体的小质量，那么可以列出微分方程：
$$\frac{d^2 s}{dt^2}=-\frac{GM}{(r+s)^2}\tag{1}$$ 并且初始条件是$t=0,s=h,\dot{s}=v=0$

在实际应用中，我们不必求出这道微分方程的精确解，因为这个解极其麻烦，在之前曾经讨论过。我们只需要求出一个有足够精确度的近似解就行。

点击阅读全文...

典型的冬季星空-KAGAYA

BoJone一看到这些图片，就不由自主地心生喜爱，觉得只有一个词语可以形容它，那就是“唯美”。是的，太美了！几乎每一张图片都把星空和动画完美地结合了起来，既极具美感，又融合了天文。极度细致的画面营造了一个仙境般的世界，加上清澈浩淼的星空、轻舞飞扬的花瓣、不食人间烟火的星之女神……，这一切结合在一起，勾起了人们对于茫茫宇宙的无限幻想，打动人们的心扉而产生共鸣。 这一切纯净而美好的幻想构筑了一个新的世界，它属于KAGAYA，同样属于喜爱这些作品的KAGAYA的拥趸，对于他们来说，那就是天堂。

点击阅读全文...

代数基本定理：任何一个一元复系数多项式都至少有一个复数根。也就是说，复数域是代数封闭的。

虽说这有其名，但却无其实，它并不是最基本的代数定理；因为在那个时候，代数基本上就是关于解实系数或复系数多项式方程，所以才被命名为代数基本定理(Fundamental theorem of algebra)。

建立在此前提上，我们可以推出：

一元复系数n次代数方程在复数范围内都有n个根（有可能是共轨复根）。

点击阅读全文...