高维空间的叉积及其几何意义
By 苏剑林 | 2013-12-26 | 57076位读者 | 引用向量之间的运算有点积和叉积(Cross Product,向量积、外积),其中点积是比较简单的,而且很容易推广到高维;但是叉积不同,一般来说它只不过是三维空间中的东西。叉积的难以推广在于它的多重含义性,如果将向量及其叉积放到张量里边来看(这属于微分形式的内容),那么三维以上的向量叉积是不存在的;但是如果只是把叉积看成是“由两个向量生成第三个与其正交的向量”的工具的话,那么叉积也是可以高维推广的,而且推广的技巧非常巧妙,与三维空间的叉积也非常相似。
回顾三维空间
为了推广三维空间的叉积,首先回顾三维空间的叉积来源是有益的。叉积起源于四元数乘法,但是从目的性来讲,我们希望构造一个向量$\boldsymbol{w}=(w_1,w_2,w_3)$,使得它与已知的两个不共线的向量$\boldsymbol{u}=(u_1,u_2,u_3),\boldsymbol{v}=(v_1,v_2,v_3)$垂直(正交)。从普适性的角度来讲,我们还希望构造出来的向量没有任何“奇点”,为此,我们只用乘法构造。至于叉积的几何意义,则是后话,毕竟,先达到基本的目的再说。
矩阵描述三维空间旋转
By 苏剑林 | 2013-12-28 | 85533位读者 | 引用本节简单介绍用矩阵来描述旋转。在二维平面上,复数无疑是描述旋转的最佳工具;然而推广到三维空间中,却要动用到“四元数”了。为了证明四元数的相关结论,我们需要三维旋转的矩阵描述。最一般的旋转运动为:绕某一根轴旋转$\theta$角度。这样我们就需要三个参数来描述它:确定一根轴至少需要两个参数,确定角度需要一个参数。因此,如果要用“数”来描述三维空间的伸缩和旋转的话,“三元数”显然是不够的,完成这一目的至少需要四元数。这也从另外一个角度反映了三元数的不存在性。
矩阵方法
首先我们认识到,如果旋转轴是坐标轴之一,那么旋转矩阵将是最简单的,比如向量$\boldsymbol{x}=(x_0,y_0,z_0)^{T}$绕$z$轴逆时针旋转$\theta$角后的坐标就可以描述为
$$\begin{equation}
\boldsymbol{R}_{\theta}\boldsymbol{x}\end{equation}$$
写在2013年即将逝去之际
By 苏剑林 | 2013-12-31 | 23773位读者 | 引用2013年即将过去,而我的大二也即将过去一半了。这一学期广播台的事情忙了很多,数学物理的进展比想象中稍微缓了一些,主要的进步是在向量分析(场论)、路径积分和微分方程等方面。下学期开始分流了,我选择了非师,但事实上,我更喜欢师范类的课程,我选择非师的唯一原因是选择师范需要修教育学和心理学。幸好,我们创新班的自由度比较多,可以自由选择下学期的课程,我选择了六门数学课程:
1、常微分方程;
2、复变函数;
(这两门纯粹是凑学分的,我觉得他能讲的东西我都懂了,而我认为很重要的部分他不讲...)
3、数理统计;
(这门主要的想法是为路径积分以及统计力学奠基)
4、微分几何;
(主要是广义相对论的奠基,还有理论物理形式)
5、偏微分方程;
(第4、5都是大三的课程,我是去跟大三一起上的)
6、离散数学。
有质动力:倒立单摆的稳定性
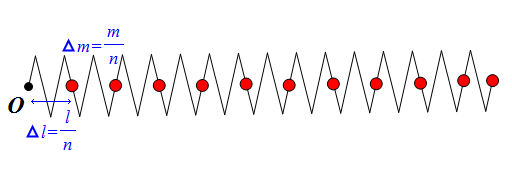
By 苏剑林 | 2013-12-29 | 48609位读者 | 引用一维弹簧的运动(上)
By 苏剑林 | 2014-03-11 | 27928位读者 | 引用视频演示:费曼的茶杯
By 苏剑林 | 2014-02-07 | 18618位读者 | 引用在学车的时候,我堂大哥曾问我一道作圆的问题:
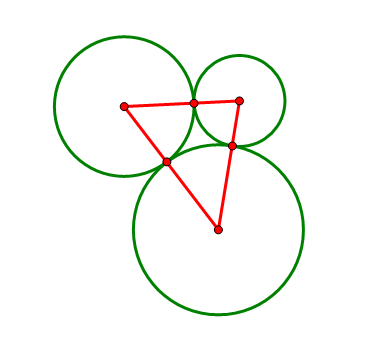
平面上给出三个两两相切的圆以及它们的圆心,求作一个圆与这三个圆都相切(尺规作图)。
如果从纯几何的途径入手,我们甚至很难判断这样的圆是否存在。但是我之前似乎已经看过类似的题目,于是很快想到一个名词:反演。反演可以将圆反演成直线(圆过反演点),也可以将圆反演成圆(圆不过反演点),而其他的相切、相交等关系保持不变。对反演后的图形进行相同的反演,就变回原来的图形。本题的难点在于圆太多,利用反演,我们可以将它变为两条直线和一个圆的问题。
假设读者已经有了反演的基本知识,如果没有,请到
http://zh.wikipedia.org/wiki/反演
阅读相关内容。









最近评论