科学空间|Scientific Spaces

去年我们放出了SimBERT模型，它算是我们开源的比较成功的模型之一，获得了不少读者的认可。简单来说，SimBERT是一个融生成和检索于一体的模型，可以用来作为句向量的一个比较高的baseline，也可以用来实现相似问句的自动生成，可以作为辅助数据扩增工具使用，这一功能是开创性的。

近段时间，我们以RoFormer为基础模型，对SimBERT相关技术进一步整合和优化，最终发布了升级版的RoFormer-Sim模型。

简介

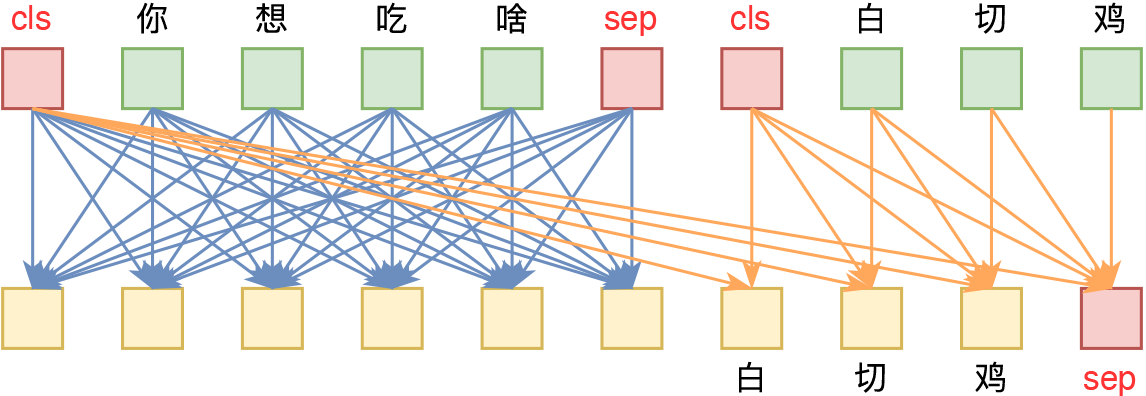
RoFormer-Sim是SimBERT的升级版，我们也可以通俗地称之为“SimBERTv2”，而SimBERT则默认是指旧版。从外部看，除了基础架构换成了RoFormer外，RoFormer-Sim跟SimBERT没什么明显差别，事实上它们主要的区别在于训练的细节上，我们可以用两个公式进行对比：
\begin{array}{c}
\text{SimBERT} = \text{BERT} + \text{UniLM} + \text{对比学习} \\[5pt]
\text{RoFormer-Sim} = \text{RoFormer} + \text{UniLM} + \text{对比学习} + \text{BART} + \text{蒸馏}\\
\end{array}

点击阅读全文...

在之前的文章《用时间换取效果：Keras梯度累积优化器》中，我们介绍过“梯度累积”，它是在有限显存下实现大batch_size效果的一种技巧。一般来说，梯度累积适用的是loss是独立同分布的场景，换言之每个样本单独计算loss，然后总loss是所有单个loss的平均或求和。然而，并不是所有任务都满足这个条件的，比如最近比较热门的对比学习，每个样本的loss还跟其他样本有关。

那么，在对比学习场景，我们还可以使用梯度累积来达到大batch_size的效果吗？本文就来分析这个问题。

简介

一般情况下，对比学习的loss可以写为
\begin{equation}\mathcal{L}=-\sum_{i,j=1}^b t_{i,j}\log p_{i,j} = -\sum_{i,j=1}^b t_{i,j}\log \frac{e^{s_{i,j}}}{\sum\limits_j e^{s_{i,j}}}=-\sum_{i,j=1}^b t_{i,j}s_{i,j} + \sum_{i=1}^b \log\sum_{j=1}^b e^{s_{i,j}}\label{eq:loss}\end{equation}
这里的$b$是batch_size；$t_{i,j}$是事先给定的标签，满足$t_{i,j}=t_{j,i}$，它是一个one hot矩阵，每一列只有一个1，其余都为0；而$s_{i,j}$是样本$i$和样本$j$的相似度，满足$s_{i,j}=s_{j,i}$，一般情况下还有个温度参数，这里假设温度参数已经整合到$s_{i,j}$中，从而简化记号。模型参数存在于$s_{i,j}$中，假设为$\theta$。

点击阅读全文...

大家都知道，Transformer的$\mathcal{O}(n^2)$复杂度是它的“硬伤”之一。不过凡事有弊亦有利，$\mathcal{O}(n^2)$的复杂度也为Transformer带来很大的折腾空间，我们可以灵活地定制不同的attention mask，来设计出不同用途的Transformer模型来，比如UniLM、K-BERT等。

本文介绍笔者构思的一个能用于文本的UniVAE模型，它沿用类似UniLM的思路，将VAE做到了一个Transformer模型里边，并且还具备多尺度特性～

UniAE式Attention关联示意图

点击阅读全文...

我们知道，梯度累积是在有限显存下实现大batch_size训练的常用技巧。在之前的文章《用时间换取效果：Keras梯度累积优化器》中，我们就简单介绍过梯度累积的实现，大致的思路是新增一组参数来缓存梯度，最后用缓存的梯度来更新模型。美中不足的是，新增一组参数会带来额外的显存占用。

这几天笔者在思考优化器的时候，突然意识到：梯度累积其实可以内置在带动量的优化器中！带着这个思路，笔者对优化了进行了一些推导和实验，最后还得到一个有意思但又有点反直觉的结论：少更新几步参数，模型最终效果可能会变好！

注：本文下面的结果，几乎原封不动且没有引用地出现在Google的论文《Combined Scaling for Zero-shot Transfer Learning》中，在此不做过多评价，请读者自行品评。

SGDM

在正式讨论之前，我们定义函数
\begin{equation}\chi_{t/k} = \left\{ \begin{aligned}&1,\quad t \equiv 0\,(\text{mod}\, k) \\
&0,\quad t \not\equiv 0\,(\text{mod}\, k)
\end{aligned}\right.\end{equation}
也就是说，$t$是一个整数，当它是$k$的倍数时，$\chi_{t/k}=1$，否则$\chi_{t/k}=0$，这其实就是一个$t$能否被$k$整除的示性函数。在后面的讨论中，我们将反复用到这个函数。

点击阅读全文...

当前，WGAN主流的实现方式包括参数裁剪（Weight Clipping）、谱归一化（Spectral Normalization）、梯度惩罚（Gradient Penalty），本来则来介绍一种新的实现方案：梯度归一化（Gradient Normalization），该方案出自两篇有意思的论文，分别是《Gradient Normalization for Generative Adversarial Networks》和《GraN-GAN: Piecewise Gradient Normalization for Generative Adversarial Networks》。

有意思在什么地方呢？从标题可以看到，这两篇论文应该是高度重合的，甚至应该是同一作者的。但事实上，这是两篇不同团队的、大致是同一时期的论文，一篇中了ICCV，一篇中了WACV，它们基于同样的假设推出了几乎一样的解决方案，内容重合度之高让我一直以为是同一篇论文。果然是巧合无处不在啊～

点击阅读全文...

在本系列的前面几篇文章中，我们已经从多个角度来理解了VAE，一般来说，用VAE是为了得到一个生成模型，或者是做更好的编码模型，这都是VAE的常规用途。但除了这些常规应用外，还有一些“小众需求”，比如用来估计$x$的概率密度，这在做压缩的时候通常会用到。

本文就从估计概率密度的角度来了解和推导一下VAE模型。

两个问题

所谓估计概率密度，就是在已知样本$x_1,x_2,\cdots,x_N\sim \tilde{p}(x)$的情况下，用一个待定的概率密度簇$q_{\theta}(x)$去拟合这批样本，拟合的目标一般是最小化负对数似然：
\begin{equation}\mathbb{E}_{x\sim \tilde{p}(x)}[-\log q_{\theta}(x)] = -\frac{1}{N}\sum_{i=1}^N \log q_{\theta}(x_i)\label{eq:mle}\end{equation}

点击阅读全文...

前两天刷到了Google的一篇论文《Step-size Adaptation Using Exponentiated Gradient Updates》，在其中学到了一些新的概念，所以在此记录分享一下。主要的内容有两个，一是非负优化的指数梯度下降，二是基于元学习思想的学习率调整算法，两者都颇有意思，有兴趣的读者也可以了解一下。

指数梯度下降

梯度下降大家可能听说得多了，指的是对于无约束函数$\mathcal{L}(\boldsymbol{\theta})$的最小化，我们用如下格式进行更新：
\begin{equation}\boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_t - \eta\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}_t)\end{equation}
其中$\eta$是学习率。然而很多任务并非总是无约束的，对于最简单的非负约束，我们可以改为如下格式更新：
\begin{equation}\boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_t \odot \exp\left(- \eta\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}_t)\right)\label{eq:egd}\end{equation}
这里的$\odot$是逐位对应相乘（Hadamard积）。容易看到，只要初始化的$\boldsymbol{\theta}_0$是非负的，那么在整个更新过程中$\boldsymbol{\theta}_t$都会保持非负，这就是用于非负约束优化的“指数梯度下降”。

点击阅读全文...

在文章《从熵不变性看Attention的Scale操作》中，我们推导了一版具有熵不变性质的注意力机制：
\begin{equation}Attention(Q,K,V) = softmax\left(\frac{\kappa \log n}{d}QK^{\top}\right)V\label{eq:a}\end{equation}
可以观察到，它主要是往Softmax里边引入了长度相关的缩放因子$\log n$来实现的。原来的推导比较繁琐，并且做了较多的假设，不利于直观理解，本文为其补充一个相对简明快速的推导。

推导过程

我们可以抛开注意力机制的背景，直接设有$s_1,s_2,\cdots,s_n\in\mathbb{R}$，定义
$$p_i = \frac{e^{\lambda s_i}}{\sum\limits_{i=1}^n e^{\lambda s_i}}$$

点击阅读全文...