《新理解矩阵2》:矩阵是什么?
By 苏剑林 | 2012-10-31 | 47795位读者 | Kimi 引用上一篇文章中我从纯代数运算的角度来讲述了我对矩阵的一个理解,可以看到,我们赋予了矩阵相应的运算法则,它就在代数、分析等领域显示出了巨大作用。但是纯粹的代数是不足够的,要想更加完美,最好是找到相应的几何对象能够与之对应,只有这样,我们才能够直观地理解它,以达到得心应手的效果。
几何理解
我假设读者已经看过孟岩的《理解矩阵》三篇文章,所以更多的细节我就不重复了。我们知道,矩阵A
$$\begin{pmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix}$$
事实上由两个向量$[a_{11},a_{21}]^T$和$[a_{12},a_{22}]^T$(这里的向量都是列向量)组成,它描述了一个平面(仿射)坐标系。换句话说,这两个向量其实是这个坐标系的两个基,而运算$y=Ax$则是告诉我们,在$A$这个坐标系下的x向量,在$I$坐标系下是怎样的。这里的$I$坐标系就是我们最常用的直角坐标系,也就是说,任何向量(包括矩阵里边的向量),只要它前面没有矩阵作用于它,那么它都是在直角坐标系下度量出来的。
《新理解矩阵1》:矩阵是什么?
By 苏剑林 | 2012-10-29 | 97144位读者 | Kimi 引用前边我承诺过会写一些关于自己对矩阵的理解。其实孟岩在《理解矩阵》这三篇文章中,已经用一种很直观的方法告诉了我们有关矩阵以及线性代数的一些性质和思想。而我对矩阵的理解,大多数也是来源于他的文章。当然,为了更好地理解线性代数,我还阅读了很多相关书籍,以求得到一种符合直觉的理解方式。孟岩的blog已经很久没有更新了,在此谨引用他的标题,来叙述我对矩阵的理解。
当然,我不打算追求那些空间、算子那些高抽象性的问题,我只是想发表一下自己对线性代数中一些常用工具的看法,比如说矩阵、行列式等。同时,文章命名为“理解矩阵”,也就是说这不是矩阵入门教程,而是与已经有一定的线性代数基础的读者一起探讨关于矩阵的其他理解方式,仅此而已。我估计基本上学过线性代数的读者都能够读懂这篇文章。
首先,我们不禁要追溯一个本源问题:矩阵是什么?
行星密度与其公转周期(更新)
By 苏剑林 | 2012-10-24 | 29674位读者 | Kimi 引用===我与《天文爱好者》不得不说的故事===
去年在订阅2012年的《天文爱好者》时,考虑到之后就要上大学了,所以只是订了半年,因此过了今年六月我就没有看新的《天文爱好者》了。暑假的两个月,还有九月、十月,将近四个月没有看它了,我本以为我已经适应了没有天爱的日子。
大概一个星期前,我在天爱的淘宝网重新买了最近四个月的《天文爱好者》,18日下午,我再见了它。那天晚上,我突然觉得很感动,有种感慨万千的感觉。虽然这么久没有看了,但是再看的感觉是如此的熟悉,如此的温馨。我原来觉得天文只是我的一个业余兴趣,如同生物化学那样,但在那瞬间我明白了我真的爱着天文,而且时间和空间的距离并不能减少我的爱!在那时,我决定了,我一定要从事天文相关专业——虽然我只是一个数学系学生!
==========行星周期下限==========
(2012.10.25:zwhzjh提出攝动力公式有错误,修正了攝动力的计算公式,之前写少了一个因子2,还有在最后的实际检验时,为了追求结果的合理性,忽略了方法的科学性,现在已经进行了修正,欢迎各位提更多意见。)
本文要探讨的东西是我在阅读《天文爱好者》的时候偶然发现的。在发现系外行星以前,人们通常都认为像木星这样的气态巨行星,公转周期都应该在十年以上。因此当瑞士天文学家米歇尔·迈耶和迪戴尔·邱洛兹发现第一颗系外行星时,他们简直无法确信自己的发现,因为这颗类木行星的公转周期只有短短的4.2天!但是经过确认,这的确是一颗系外行星,颠覆了过去的看法。我饶有兴致地研究下去,企图推导出某一密度行星的公转周期下限。
各位读者不妨先估计一下,它会与什么物理量有关?行星质量?母星质量?还是...?
分享:孟岩的《理解矩阵》一文
By 苏剑林 | 2012-10-22 | 70602位读者 | Kimi 引用之前已经提到我要自学相对论和量子力学。作为现代物理的两大支柱,所用的数学也是很“现代”的,不能总是用高中那套简单的模式来计算,所以线性代数是我要熟悉的一门课程之一。现在大一还没开设线性代数课程,但是我所持的观点是:“任何东西只要你需要它,你就应该去学,而且能够学会。”其实我初三暑假的时候就开始接触了线性代数,我看的那本教材,跟国内其他线性代数教材一样,采用了一种只要求记忆和计算的方式来教授,先讲从线性方程组引出行列式,再到矩阵。我那时也在背诵,知道了了行列式怎么算的,行列式可以用来解方程组,矩阵是怎么相乘的等等。但我完全不知道为什么,我甚至不懂为什么这门课程叫“线性代数”。(当然,也有可能是那时的数学水平不够)国外很多教程都讲的很好,很规范地教,但是对于国内像我这样平庸的学生又显得过于专业。我一直期待有这样的一个平衡点,可惜一直没有找到,所以只能从各种渠道摸索。
证明光速不变的一个理想实验??
By 苏剑林 | 2012-10-18 | 82263位读者 | Kimi 引用在狭义相对论发表之前和之后,都有不少实验从不同角度论证了它的正确性。这些实验大多数是实际测量得出结果的,当然也存在着一些“理想实验”,这些实验只需要一定的逻辑推理,而实际上是无法完成的。下面就是我很久之前在某本书(很抱歉,我真的忘记书名了)看到的一个用来推翻光速可叠加的伽利略变换的理想实验。它只用寥寥几句,就好像已经证明了“c+c=c”(c是真空中的光速)的事实。可是“c+c=c”在狭义相对论上是作为原理出现的,是不可能通过逻辑推理来证明的。事实究竟如何?我们先来看这个实验。
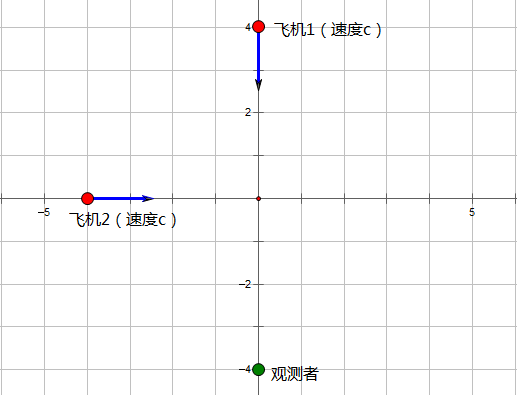
任意选定一个坐标原点。设想原点的正北方$c\cdot t_0$处有一架以光速$c$朝南运行的飞机1;原点的正西方$c\cdot t_0$处有一架以光速$c$朝东运行的飞机2。假设就这样匀速运动着,显然,$t_0$时间后,将会发生惨剧(飞机相撞)。
相对论和量子力学的初探
By 苏剑林 | 2012-10-16 | 42749位读者 | Kimi 引用=====大学学习=====
上大学已经一个多月了,除去军训的两周和国庆放假的一周,到现在已经是第三周上课了。我是数学专业的,由于是那个勷勤创新班,它希望我们都向研究型数学的方向发展,所以给我们“更多的自由研究时间”,所以课程比一般的班还少一点。由于高中已经对高等数学有个大概的了解,所以一开始让很多同学都喊苦的数学分析、解析几何于我而言都还是比较容易接受的。但从另外一个角度上来讲,我感觉我学得快的原因,倒不全是以前的积累,而是因为个人的学习方式。我不喜欢跟着老师的步伐走,我喜欢而且需要深入地思考和理解一个问题,希冀达到一理通百理明的效果,而不是做完一题紧接着下一题。因为我认为这种竞赛式的学习不能给我们带来实质性的进步,而且有可能抹杀了我们的创造力。
没有应用的数学是很枯燥乏味的,数学不能脱离物理、化学等领域。当然“应用”这个词有很广泛的意思,它不一定在实际生活中起到了立竿见影的作用,而是所有在非数学领域中体现了数学之美的例子都可以叫做数学应用,或者有趣的数学。所以,在经历了一两周纯粹地研究数学之后,我感觉我不能再这样下去了,与其零散地涉猎各个方面的知识,倒不如现在开始就系统地学习一些学科以外的科学知识。于是,我决定重拾高中还没有完成的事情——学习相对论和量子力学——所谓现代物理的两大支柱。
中国第一个诺贝尔奖得主
By 苏剑林 | 2012-10-11 | 68309位读者 | Kimi 引用2012诺贝尔奖...
By 苏剑林 | 2012-10-11 | 47383位读者 | Kimi 引用又是一年诺奖公布时......每年的这个时候,诺贝尔奖又会被热门地提及到,现在三个自然科学方面的奖项都已经公开了。简略收集如下:
诺贝尔生理学或医学奖
京都大学物质-细胞统合系统据点iPS细胞研究中心主任长山中伸弥(Shinya Yamanaka)、英国发育生物学家约翰-戈登因(John B. Gurdon)。
原因:在细胞核重新编程研究领域的杰出贡献而获奖。所谓细胞核重编程即将成年体细胞重新诱导回早期干细胞状态,以用于形成各种类型的细胞,应用于临床医学。细胞核重编程指细胞内的基因表达由一种类型变成另一种类型。通过这一技术,可在同一个体上将较容易获得的细胞(如皮肤细胞)类型转变成另一种较难获得的细胞类型(如脑细胞)。这一技术的实现将能避免异体移植产生的排异反应。







 感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持!
感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持! 科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。
科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。 





最近评论