漫话模型|模型与选芒果
By 苏剑林 | 2015-07-15 | 48189位读者 | 引用很多人觉得“模型”、“大数据”、“机器学习”这些字眼很高大很神秘,事实上,它跟我们生活中选水果差不了多少。本文用了几千字,来试图教会大家怎么选芒果...
模型的比喻
假如我要从一批芒果中,找出好吃的那个来。而我不能直接切开芒果尝尝,所以我只能观察芒果,能观察到的量有颜色、表面的气味、大小等等,这些就是我们能够收集到的信息(特征)。
生活中还要很多这样的例子,比如买火柴(可能年轻的城里人还没见过火柴?),如何判断一盒火柴的质量?难道要每根火柴都划划,看看着不着火?显然不行,我们最多也只能划几根,全部划了,火柴也不成火柴了。当然,我们还能看看火柴的样子,闻闻火柴的气味,这些动作是可以接受的。
用Pandas实现高效的Apriori算法
By 苏剑林 | 2015-07-02 | 176458位读者 | 引用最近在做数据挖掘相关的工作,阅读到了Apriori算法。平时由于没有涉及到相关领域,因此对Apriori算法并不了解,而如今工作上遇到了,就不得不认真学习一下了。Apriori算法是一个寻找关联规则的算法,也就是从一大批数据中找到可能的逻辑,比如“条件A+条件B”很有可能推出“条件C”(A+B-->C),这就是一个关联规则。具体来讲,比如客户买了A商品后,往往会买B商品(反之,买了B商品不一定会买A商品),或者更复杂的,买了A、B两种商品的客户,很有可能会再买C商品(反之也不一定)。有了这些信息,我们就可以把一些商品组合销售,以获得更高的收益。而寻求关联规则的算法,就是关联分析算法。
啤酒与尿布
关联算法的案例中,最为人老生常谈的应该是“啤酒与尿布”了。“啤酒与尿布”的故事产生于20世纪90年代的美国沃尔玛超市中,超市管理人员发现“啤酒与尿布两件看上去毫无关系的商品会经常出现在同一个购物篮中”。经过分析,原来在美国有婴儿的家庭中,一般是母亲在家中照看婴儿,年轻的父亲前去超市购买尿布。父亲在购买尿布的同时,往往会顺便为自己购买啤酒,这样就会出现啤酒与尿布这两件看上去不相干的商品经常会出现在同一个购物篮的现象。因此,沃尔玛尝试将啤酒与尿布摆放在相同的区域,让年轻的父亲可以同时找到这两件商品。事实是效果相当不错!
文本情感分类(一):传统模型
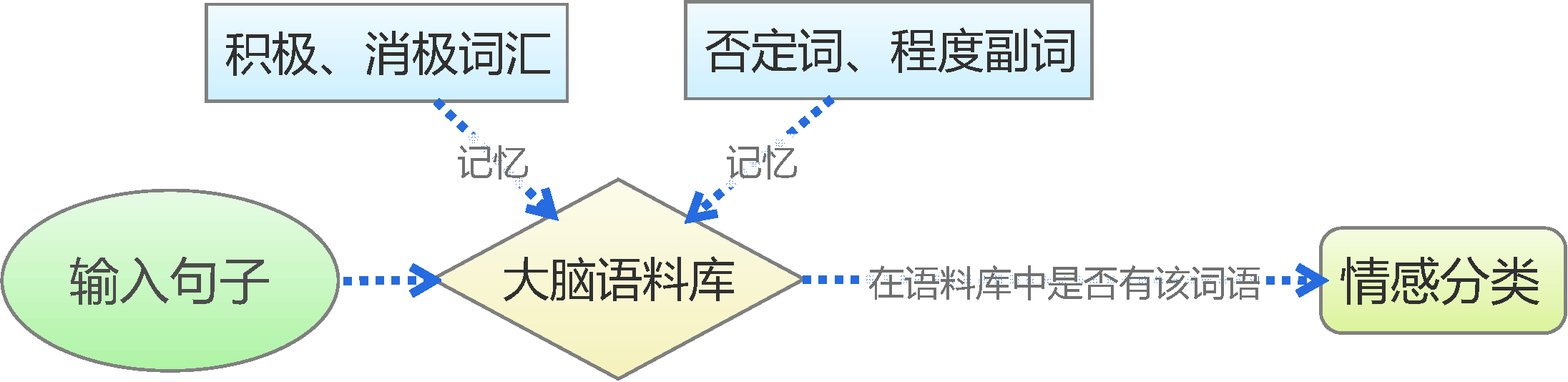
By 苏剑林 | 2015-06-22 | 300729位读者 | 引用前言:四五月份的时候,我参加了两个数据挖掘相关的竞赛,分别是物电学院举办的“亮剑杯”,以及第三届 “泰迪杯”全国大学生数据挖掘竞赛。很碰巧的是,两个比赛中,都有一题主要涉及到中文情感分类工作。在做“亮剑杯”的时候,由于我还是初涉,水平有限,仅仅是基于传统的思路实现了一个简单的文本情感分类模型。而在后续的“泰迪杯”中,由于学习的深入,我已经基本了解深度学习的思想,并且用深度学习的算法实现了文本情感分类模型。因此,我打算将两个不同的模型都放到博客中,供读者参考。刚入门的读者,可以从中比较两者的不同,并且了解相关思路。高手请一笑置之。
基于情感词典
【翻译】巨型望远镜:要继续,就得有牺牲!
By 苏剑林 | 2015-06-10 | 33460位读者 | 引用文章来自:新科学家,这是一篇关于30米望远镜(Thirty Meter Telescope,TMT)的新闻,起因是望远镜的制造遭到当地人的不满,当然背后的原因是很深远的,难以说清楚。更多有关TMT的新闻,可以阅读:http://www.ctmt.org/
夏威夷的巨型望远镜:要继续,就得有牺牲!
四分之一必须离开!在停止了两个月之后,夏威夷的巨型30米望远镜(Thirty Meter Telescope,TMT)重新回归到建设进程——但要牺牲其他望远镜。
由于夏威夷当地居民的抗议声越来越大,早在四月望远镜的建设工作就被迫暂停。与该望远镜相比,目前世界上所有的望远镜都相形见绌——它让能够让天文学家们凝视可见的宇宙的边缘。它位于许多夏威夷人认为是“神圣之地”的死火山莫纳克亚山,因此被夏威夷人认为是一种侮辱——尤其是在山顶已经有十多个望远镜了。
收到新版《量子力学与路径积分》
By 苏剑林 | 2015-06-06 | 49382位读者 | 引用今天收到高教出版社的王超编辑寄来的费曼著作新版《量子力学与路径积分》了,兴奋ing...
《量子力学与路径积分》是费曼的一本经典著作,更是量子力学的经典著作——它是我目前读过的唯一一本从路径积分出发、并且以路径积分为第一性原理的量子力学著作(徐一鸿的《简明量子场论》好象是我读过的唯一一本纯粹以路径积分为方法的量子场论著作,也非常不错),其它类型的量子力学著作,也有部分谈到路径积分,但无一不是从哈密顿形式中引出路径积分的,在那种情况之下,路径积分只能算是一个推论。但是路径积分明明就作为量子力学的三种形式之一,它应该是可以作为量子力学的基本原理来提出的,而不应该作为另一种形式的推论。费曼做了尝试——从路径积分出发讲解量子力学,而且显然这种尝试是很成功的,至少对于我来说,路径积分是一种非常容易理解的量子力学形式。(这也许跟我的数学基础有关)
闲聊:神经网络与深度学习
By 苏剑林 | 2015-06-06 | 99558位读者 | 引用在所有机器学习模型之中,也许最有趣、最深刻的便是神经网络模型了。笔者也想献丑一番,说一次神经网络。当然,本文并不打算从头开始介绍神经网络,只是谈谈我对神经网络的个人理解。如果希望进一步了解神经网络与深度学习的朋友,请移步阅读下面的教程:
http://deeplearning.stanford.edu/wiki/index.php/UFLDL教程
http://blog.csdn.net/zouxy09/article/details/8775360
机器分类
这里以分类工作为例,数据挖掘或机器学习中,有很多分类的问题,比如讲一句话的情况进行分类,粗略点可以分类为“积极”或“消极”,精细点分为开心、生气、忧伤等;另外一个典型的分类问题是手写数字识别,也就是将图片分为10类(0,1,2,3,4,5,6,7,8,9)。因此,也产生了很多分类的模型。
【备忘】维基百科与DNSCrypt
By 苏剑林 | 2015-05-30 | 54687位读者 | 引用中文维基百科的域名zh.wikipedia.org于5月19日被关键字屏蔽和DNS污染,目前从中国已无法访问中文维基百科,中文维基百科的域名也无法解析出正确的IP地址,而英文维基百科目前未受影响,可以正常访问。
胡闹的胜利:将算子引入级数求和
By 苏剑林 | 2015-05-26 | 28530位读者 | 引用在文章《有趣的求极限题:随心所欲的放缩》中,读者“最近倒了”提出了一个新颖的解法,然而这位读者写得并非特别清晰,更重要的是里边的某些技巧似乎是笔者以前没有见过的,于是自行分析了一番,给出了以下解释。
胡闹的结果
假如我们要求级数和
$$\sum_{k=0}^n \binom{n}{k}\frac{A_k}{n^k}$$
这里$A_0=1$。一般而言,我们用下标来标注不同的数,如上式的$A_k,\,k=0,1,2,\dots$,可是有的人偏不喜欢,他们更喜欢用上标来表示数列中的各项,他们把上面的级数写成
$$\sum_{k=0}^n \binom{n}{k}\frac{A^k}{n^k}$$
可能读者就会反对了:这不是胡闹吗,这不是让它跟分母的n的k次幂混淆了吗?可是那人干脆更胡闹一些,把级数写成
$$\sum_{k=0}^n \binom{n}{k}\frac{A^k}{n^k}=\left(1+\frac{A}{n}\right)^n$$
看清楚了吧?他干脆把$A$当作一个数来处理了!太胡闹了,$A$是个什么东西?估计这样的孩子要被老师赶出课堂的了。
可是换个角度想想,似乎未尝不可。












最近评论