基于CNN的阅读理解式问答模型:DGCNN
By 苏剑林 | 2018-04-15 | 564882位读者 |2019.08.20更新:开源了一个Keras版(https://kexue.fm/archives/6906)
早在年初的《Attention is All You Need》的介绍文章中就已经承诺过会分享CNN在NLP中的使用心得,然而一直不得其便。这几天终于下定决心来整理一下相关的内容了。
背景 #
事不宜迟,先来介绍一下模型的基本情况。
模型特点 #
本模型——我称之为DGCNN——是基于CNN和简单的Attention的模型,由于没有用到RNN结构,因此速度相当快,而且是专门为这种WebQA式的任务定制的,因此也相当轻量级。SQUAD排行榜前面的模型,如AoA、R-Net等,都用到了RNN,并且还伴有比较复杂的注意力交互机制,而这些东西在DGCNN中基本都没有出现。
这是一个在GTX1060上都可以几个小时训练完成的模型!
DGCNN,全名为Dilate Gated Convolutional Neural Network,即“膨胀门卷积神经网络”,顾名思义,融合了两个比较新的卷积用法:膨胀卷积、门卷积,并增加了一些人工特征和trick,最终使得模型在轻、快的基础上达到最佳的效果。在本文撰写之时,本文要介绍的模型还位于榜首,得分(得分是准确率与F1的平均)为0.7583,而且是到目前为止唯一一个一直没有跌出前三名、并且获得周冠军次数最多的模型。
比赛情况 #
其实这个模型是我代表“广州火焰科技有限公司”来参加CIPS-SOGOU问答比赛的产物。这个比赛在去年十月份开始,然而有点虎头蛇尾,到现在依然还是不上不下的(没有结束的迹象,也没有继续新任务的迹象)。
其实刚开始的两三个月,竞争还是蛮激烈的,很多公司和大学都提交了模型,排行榜一直不断刷新。所以我觉得SOGOU这样虎头蛇尾未免有点对不起大家当初提交的热情。最关键是,它究竟是有什么计划、有什么变动,包括比赛的结束时间,一直都没公开发出什么通知,就一直把选手晾在那里。我后来打听到,截止时间是今年的CIPS举办前...一个比赛持续举办一年??
赛题简述 #
到目前为止,SOGOU的这个比赛只举办了事实类的部分,而事实类的部分基本上是跟百度之前开放的WebQA语料集一样的,即“一个问题 + 多段材料”的格式,希望从多段材料中共同决策出问题的精准答案(一般是一个实体片段)。
问题:社保缴纳多少年可以领养老金
答案:15年
材料1:最好不辞,交够15年到退休就可以领养老金了如果有特殊原因非要辞,可以个人接着交。
材料2:你好!养老保险缴纳满15年,达到退休年龄可以领取养老金。
材料3:在生活中,每个人都会缴纳社保,多少年可以领取退休... 社保要交多少年才能领养老金 呢,在上文中为大家介绍了一下。
相比WebQA,搜狗提供的训练集噪声大得多,这也使得预测难度加大。此外,我认为这种WebQA式的任务是偏向于检索匹配以及初步的语义理解技术,跟国外类似的任务SQUAD(一段长材料 + 多个问题)是有比较大的区别的,SQUAD的语料中,部分问题还涉及到了比较复杂的推理,因此SQUAD排行榜前面的模型都比较复杂、庞大。
模型 #
现在我们正式进入模型的介绍中~
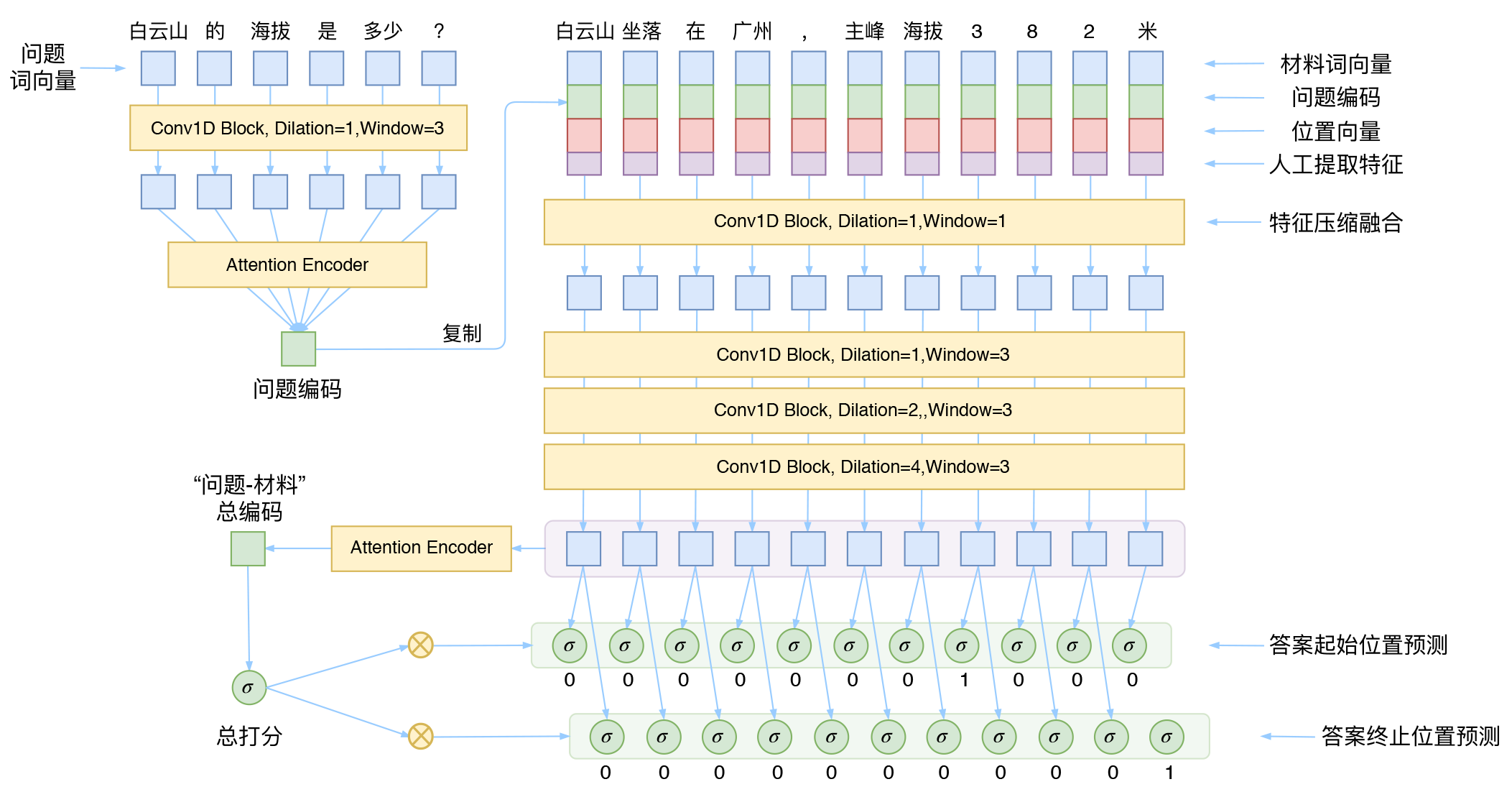
架构总览 #
先来看个模型总图
从示意图可以看到,作为一个“阅读理解”、“问答系统”模型,图中的模型几乎是简单到不能再简单了。
模型的整体架构源于WebQA的参考论文《Dataset and Neural Recurrent Sequence Labeling Model for Open-Domain Factoid Question》。这篇论文有几个特点:
1、直接将问题用LSTM编码后得到“问题编码”,然后拼接到材料的每一个词向量中;
2、人工提取了2个共现特征;
3、将最后的预测转化为了一个序列标注任务,用CRF解决。
而DGCNN基本上就是沿着这个思路设计的。我们的不同点在于
1、把原模型中所有的LSTM部分都替换为CNN;
2、提取了更丰富的共现特征(8个);
3、去掉CRF,改为“0/1标注”来分开识别答案的开始和终止位置,这可以看成一种“半指针半标注”的结构。
卷积结构 #
这部分我们来对图中的Conv1D Block进行解析。
门机制 #
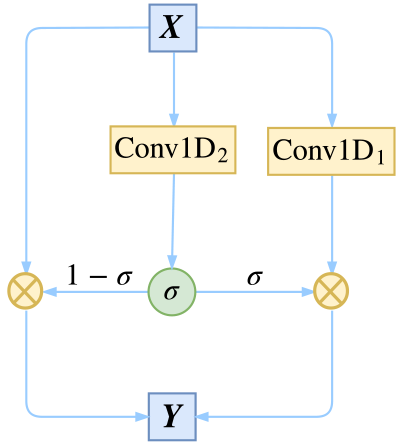
模型中采用的卷积结构,来自FaceBook的《Convolutional Sequence to Sequence Learning》,而在《分享一个slide:花式自然语言处理》一文中也提到过。假设我们要处理的向量序列是$\boldsymbol{X}=[\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_n]$,那么我们可以给普通的一维卷积加个门:
$$\boldsymbol{Y}=\text{Conv1D}_1(\boldsymbol{X}) \otimes \sigma\Big(\text{Conv1D}_2(\boldsymbol{X})\Big)\tag{1}$$
注意这里的两个Conv1D形式一样(比如卷积核数、窗口大小都一样),但权值是不共享的,也就是说参数翻倍了,其中一个用sigmoid函数激活,另外一个不加激活函数,然后将它们逐位相乘。因为sigmoid函数的值域是$(0,1)$,所以直觉上来看,就是给Conv1D的每个输出都加了一个“阀门”来控制流量。这就是GCNN的结构了,或者可以将这种结构看成一个激活函数,称为GLU(Gated Linear Unit)。
除了有直观的意义外,用GCNN的一个好处是梯度消失的风险更低,因为有一个卷积是不加任意激活函数的,没加激活函数的这部分卷积不容易梯度消失。如果输入和输出的维度大小一致,那么我们就把输入也加到里边,即使用残差结构:
$$\boldsymbol{Y}=\boldsymbol{X} + \text{Conv1D}_1(\boldsymbol{X}) \otimes \sigma\Big(\text{Conv1D}_2(\boldsymbol{X})\Big)\tag{2}$$
值得一提的是,我们使用残差结构,并不只是为了解决梯度消失,而是使得信息能够在多通道传输。我们可以将上式改写为更形象的等价形式,以便我们更清晰看到信息是如何流动的:
$$\begin{aligned}\boldsymbol{Y}=&\boldsymbol{X}\otimes \Big(1-\boldsymbol{\sigma}\Big) + \text{Conv1D}_1(\boldsymbol{X}) \otimes \boldsymbol{\sigma}\\
\boldsymbol{\sigma} =& \sigma\Big(\text{Conv1D}_2(\boldsymbol{X})\Big)
\end{aligned}\tag{3}$$
从$(3)$式中我们能更清楚看到信息的流向:以$1-\sigma$的概率直接通过,以$\sigma$的概率经过变换后才通过。这个形式非常像递归神经网络中的GRU模型。
补充推导:
$$\begin{aligned}\boldsymbol{Y}=&\boldsymbol{X}\otimes \Big[1-\sigma\Big(\text{Conv1D}_2(\boldsymbol{X})\Big)\Big] + \text{Conv1D}_1(\boldsymbol{X}) \otimes \sigma\Big(\text{Conv1D}_2(\boldsymbol{X})\Big)\\
=&\boldsymbol{X} + \Big(\text{Conv1D}_1(\boldsymbol{X}) - \boldsymbol{X}\Big)\otimes \sigma\Big(\text{Conv1D}_2(\boldsymbol{X})\Big)
\end{aligned}$$由于$\text{Conv1D}_1$并没有加激活函数,所以它只是一个线性变换,从而$\text{Conv1D}_1(\boldsymbol{X}) - \boldsymbol{X}$可以结合在一起,等效于单一一个$\text{Conv1D}_1$。说白了,在训练过程中,$\text{Conv1D}_1(\boldsymbol{X}) - \boldsymbol{X}$能做到的事情,$\text{Conv1D}_1(\boldsymbol{X})$也能做到。从而$(2)$和$(3)$两者是等价的。
膨胀卷积 #
接下来,为了使得CNN模型能够捕捉更远的的距离,并且又不至于增加模型参数,我们使用了膨胀卷积。
普通卷积跟膨胀卷积的对比,可以用一张图来演示
同样是三层的卷积神经网络(第一层是输入层),窗口大小为3。普通卷积在第三层时,每个节点只能捕捉到前后3个输入,而跟其他输入完全不沾边。
而膨胀卷积在第三层时则能够捕捉到前后7个输入,但参数量和速度都没有变化。这是因为在第二层卷积时,膨胀卷积跳过与中心直接相邻的输入,直接捕捉中心和次相邻的输入(膨胀率为2),也可以看成是一个“窗口大小为5的、但被挖空了两个格的卷积”,所以膨胀卷积也叫空洞卷积(Atrous Convolution)。在第三层卷积时,则连续跳过了三个输入(膨胀率为4),也可以看成一个“窗口大小为9、但被挖空了6个格的卷积”。而如果在相关的输入输出连一条线,就会发现第三层的任意一个节点,跟前后7个原始输入都有联系。
按照“尽量不重不漏”的原则,膨胀卷积的膨胀率一般是按照1、2、4、8、...这样的几何级数增长。当然,这里指明了是“尽量”,因为还是有些重复的。这个比例参考了Google的wavenet模型。
Block #
现在就可以解释模型图中的各个Conv1D Block了,如果输入跟输出维度大小一致时,那么就是膨胀卷积版的$(3)$式;如果输出跟输出维度大小不一致时,就是简单的$(1)$式,窗口大小和膨胀率在图上都已经注明。
注意力 #
从模型示意图可以看到,本文的DGCNN模型中,Attention主要用于取代简单的Pooling来完成对序列信息的整合,包括将问题的向量序列编码为一个总的问题向量,将材料的序列编码为一个总的材料向量。这里使用的Attention稍微不同于《Attention is All You Need》中的Attention,本文这种Attention可以认为是一种“加性注意力”,形式为
$$\begin{aligned}\boldsymbol{x}&=\text{Ecndoer}\big(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_n\big)=\sum_{i=1}^n \lambda_i \boldsymbol{x}_i\\
\lambda_i&=\mathop{\text{softmax}}_i\Big(\boldsymbol{\alpha}^{\top}\,\text{Act}\big(\boldsymbol{W}\boldsymbol{x}_i\big)\Big)\end{aligned}\tag{4}$$
这里的$\boldsymbol{\alpha},\boldsymbol{W}$都为可训练参数。而$\text{Act}$为激活函数,一般会取$\tanh$,也可以考虑$\text{swish}$函数。注意用$\text{swish}$时,最好把偏置项也加上去,变为
$$\lambda_i=\mathop{\text{softmax}}_i\Big(\boldsymbol{\alpha}^{\top}\,\text{Act}\big(\boldsymbol{W}\boldsymbol{x}_i+\boldsymbol{b}\big)+\beta\Big)\tag{5}$$
这种Attention的方案参考自R-Net模型。(注:不一定是R-Net首创,只是我是从R-Net中学来的。)
位置向量 #
为了增强CNN的位置感,我们还补充了位置向量,拼接到材料的每个词向量中。位置向量的构造方法直接沿用《Attention is All You Need》中的方案:
$$\left\{\begin{aligned}&PE_{2i}(p)=\sin\Big(p/10000^{2i/{d_{pos}}}\Big)\\
&PE_{2i+1}(p)=\cos\Big(p/10000^{2i/{d_{pos}}}\Big)
\end{aligned}\right.\tag{6}$$
输出设计 #
这部分是我们整个模型中颇具特色的地方。
思路分析 #
到现在,模型的整体结构应该已经呈现出来了。首先我们通过卷积和注意力把问题编码为一个固定的向量,这个向量拼接到材料的每个词向量中,并且还拼接了位置向量、人工特征。这时候我们得到了一个混合了问题、材料信息的特征序列,直接对这个序列进行处理即可,所以后面接了几层卷积进行编码处理,然后直接对序列进行标注,而不需要再对问题进行交互了。
在SQUAD的评测中,材料是肯定有答案的,并且答案所在的位置也做好了标注,所以SQUAD的模型一般是对整个序列做两次softmax,来预测答案的开始位置和终止位置,我们一般称之为“指针网络”。然而我们这里的WebQA式问答,材料中不一定有答案,所以我们不用softmax,而是对整个序列都用sigmoid,这样既允许了材料中没有答案,也允许答案在材料中多次出现。
双标注输出 #
既然用到标注,那么理论上最简单的方案是输出一个0/1序列:直接标注出材料中的每个词“是(1)”或“否(0)”答案。然而,这样的效果并不好,因为一个答案可能由连续多个不同的词组成,要让模型将这些不同的词都有同样的标注结果,有可能“强模型所难”。于是我们还是用两次标注的方式,来分别标注答案的开始位置和终止位置。
$$\begin{aligned}p^{start}_i = \sigma\Big(\boldsymbol{\alpha}_1^{\top}\,\text{Act}\big(\boldsymbol{W}_1\boldsymbol{x}_i+\boldsymbol{b}_1\big)+\beta_1\Big)\\
p^{end}_i = \sigma\Big(\boldsymbol{\alpha}_2^{\top}\,\text{Act}\big(\boldsymbol{W}_2\boldsymbol{x}_i+\boldsymbol{b}_2\big)+\beta_2\Big)\end{aligned}\tag{7}$$
这样一来,模型的输出设计跟指针方式和纯序列标注都不一样,或者说是两者的简化及融合。
大局观 #
最后,为了增加模型的“大局观”,我们将材料的序列编码为一个整体的向量,然后接一个全连接层来得到一个全局的打分,并把这个打分的结果乘到前面的标注中,即变成
$$\begin{aligned}\boldsymbol{o}=&\text{Ecndoer}\big(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_n\big)\\
p^{global}=&\sigma\Big(\boldsymbol{W}\boldsymbol{o}+\boldsymbol{b}\Big)\\
p^{start}_i =& p^{global}\cdot\sigma\Big(\boldsymbol{\alpha}_1^{\top}\,\text{Act}\big(\boldsymbol{W}_1\boldsymbol{x}_i+\boldsymbol{b}_1\big)+\beta_1\Big)\\
p^{end}_i =& p^{global}\cdot\sigma\Big(\boldsymbol{\alpha}_2^{\top}\,\text{Act}\big(\boldsymbol{W}_2\boldsymbol{x}_i+\boldsymbol{b}_2\big)+\beta_2\Big)\end{aligned}\tag{8}$$
这个全局打分对模型的收敛和效果具有重要的意义,它的作用是更好地判断材料中是否存在答案,一旦材料中没有答案,直接让$p^{global}=0$即可,不用“煞费苦心”让每个词的标注都为0。
人工特征 #
文章的前面部分,我们已经多次提到过人工特征,那么这些人工特征的作用有多大呢?简单目测的话,这几个人工特征对于模型效果的提升可能超过2%!可见设计好的特征对模型效果的特征、模型复杂度的降低,都有着重要的作用。
人工特征是针对材料中的词来设计的,列举如下(Q即question,代表问题;E即evidence,代表材料)。
Q-E全匹配 #
也就是判断材料中的词是否在问题出现过,出现过则为1,没出现过则为0。这个特征的思路是直接告诉模型问题中的词在材料中什么地方出现了,那些地方附近就很有可能有答案。这跟我们人类做阅读理解的思路是吻合的。
E-E共现 #
这个特征是计算某个材料中的词在其他材料中的出现比例。比如有10段材料,第一段材料有一个词w,在其余九段材料中,有4段都包含了这个词,那么第一段材料的词w就获得一个人工特征4/10。
这个特征的思路是一个词出现在的材料越多,这个词越有可能是答案。
Q-E软匹配 #
以问题大小为窗口来对材料的每个窗口算Jaccard相似度、相对编辑距离。
比如问题“白云山 的 海拔 是 多少 ?”,材料“白云山 坐落 在 广州 , 主峰 海拔 3 8 2 米”。问题有6个词,那么窗口大小就为6,将材料拆分为:
X X X 白云山 坐落 在
X X 白云山 坐落 在 广州
X 白云山 坐落 在 广州 ,
白云山 坐落 在 广州 , 主峰
坐落 在 广州 , 主峰 海拔
在 广州 , 主峰 海拔 3
广州 , 主峰 海拔 3 8
, 主峰 海拔 3 8 2
主峰 海拔 3 8 2 米
海拔 3 8 2 米 X
3 8 2 米 X X
其中X代表占位符。有了这个拆分,我就可以算每一块与问题的Jaccard相似度了,将相似度的结果作为当前词(也就是红色词)的一个特征,上述例子算得[0.13, 0.11, 0.1, 0.09, 0.09, 0.09, 0.09, 0.09, 0.09, 0.1, 0]。
同样地,我们还可以算每一块与问题的编辑距离,然后除以窗口大小,就得到一个0~1之间的数,我称之为“相对编辑距离”,上述例子算得[0.83, 0.83, 0.83, 0.83, 1, 1, 1, 0.83, 1, 1, 1]。
Jaccard相似度是无序的,而编辑距离是有序的,因此这两个做法相对于从有序和无序两个角度来衡量问题和材料之间的相似度。这两个特征的思路跟第一个特征一样,都是告诉模型材料中哪部分会跟问题相似,那部分的附近就有可能有答案。
这两个特征的主要思路来自Keras群中的Yin神,感谢~
字符特征 #
SQUAD排名靠前的模型中,基本都是以词向量和字符向量共同输入到模型中的,而为了提升效果,我们似乎也要把字向量和词向量同时输入。但我们并不想将模型做得太庞大,于是我们在人工特征这里,加入了字符级特征。
其实思路也很简单,前面介绍的4个特征,都是以词为基本单位来计算的,事实上也可以以字为基本单位算一次,然后把每个词内的字的结果平均一下,作为词的特征就行了。比如在“Q-E全匹配”特征中,假设问题只有“演”这个词,而材料则有“合演”这个词,如果按照词来看,“合演”这个词没有在问题出现过,所以共现特征为0,而如果考虑字的话,“合演”就被拆开为两个字“合”和“演”,按照同样的方式算共现特征,“合”得到0、“演”得到1,将两者平均一下,得到0.5,作为“合演”这个词的字符级“Q-E全匹配”特征。
其他三个特征也同样处理,这样我们就得到了另外4个特征,一定得到8个人工特征。
实现 #
现在,模型的各个部分基本上都解释清楚了。其实模型整体简单明了,讲起来也容易,应该会有种“大道至简”的感觉。下面介绍一些实现要点。
模型设置 #
下面是实现模型的一些基本要点。
中文分词 #
从前面的介绍中可以看到,本模型是基于词来实现的,并且基于前面说的人工特征简单引入了字符级别的信息。不过,为了使得模型整体上更加灵活,能够应答更多的问题,本文仅仅对输入进行了一个基本的分词,使得分词的颗粒度尽量低一些。
具体实现为:自己写了一个基于一元模型的分词模块,自行准备了一个约50万词的词典,而所有的英文、数字都被拆开为单个的字母和数字,比如apple就变成了五个“词”:a p p l e,382就变成了三个“词”:3 8 2。
由于没有新词发现功能,这样一来,整个词表的词就不会超过50万。事实上,我们最后得到的模型,模型总词数只有30万左右。
当然,读者可以使用结巴分词,关闭结巴分词的新词发现,并且手动对数字和英文进行拆分,效果是一样的。
部分参数 #
1、词向量的维度为128维,由比赛方提供的训练语料、WebQA语料、50万百度百科条目、100万百科知道问题用Word2Vec预训练而成,其中Word2Vec的模型为Skip Gram,窗口为5,负采样数为8,迭代次数为8,训练时间约为12小时;
2、填充词向量取全零向量,词向量在DGCNN模型的训练过程中保持固定;
3、所有Conv1D的输出维度皆为128维,位置向量也是128维;
4、序列的最大长度取为100,如果一个batch中某些样本涉及到padding,那么对padding部分要做好mask;
5、由于最后变成一个二分类的标注形式,并且考虑到正负类不均衡,使用二分类的focal loss作为损失函数;
6、用adam优化器进行训练,先用$10^{-3}$的学习率训练到最优(大概6个epoch内),然后加载最优模型,改用$10^{-4}$学习率训练到最优(3个epoch内)。
正则项 #
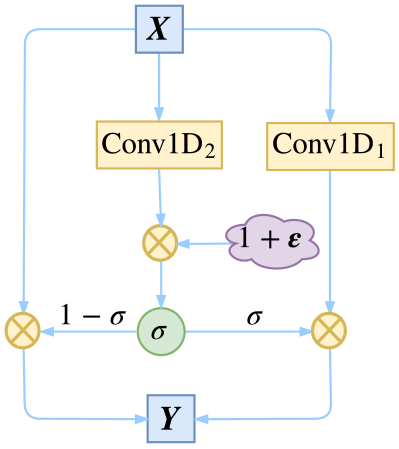
在比赛后期,我们发现一种类似DropPath的正则化能轻微提升效果,不过提升幅度我也不大确定,总之当时是带来了一定的提升。
这个正则化手段建立在$(3)$式的基础上,我们的思路是在训练阶段对“门”进行扰动:
$$\begin{aligned}\boldsymbol{Y}=&\boldsymbol{X}\otimes \Big(1-\boldsymbol{\sigma}\Big) + \text{Conv1D}_1(\boldsymbol{X}) \otimes \boldsymbol{\sigma}\\
\boldsymbol{\sigma} =& \sigma\Big(\text{Conv1D}_2(\boldsymbol{X})\otimes (1 + \boldsymbol{\varepsilon})\Big)
\end{aligned}\tag{9}$$
其中$\boldsymbol{\varepsilon}$是$[-0.1, 0.1]$内的均匀随机数张量。这样一来,我们给GCNN的“门”加入了“乘性噪声”来使得具有更好的鲁棒性(对抗参数的小扰动)。
这个正则化方案的提出,多多少少受到了《FractalNet: Ultra-Deep Neural Networks without Residuals》和《Shake-Shake regularization》里边的正则化技术启发。
数据准备 #
数据预处理 #
由于SOGOU这个比赛允许使用外部数据,因此我们及大多数参赛队伍都使用了WebQA数据集补充训练。考虑到WebQA数据集相对规整一些,而SOGOU提供的语料噪声相对大一些,所以我们将SOGOU和WebQA的语料集以2:1的比例混合。
不管是WebQA还是SOGOU,所提供的语料都是“一个问题 + 多段材料 + 一个答案”的形式,并没有特别指明答案出现在哪段材料的哪个位置。因此,我们只好把材料中所有能跟答案全匹配的子串都视为答案所在处。对于某些样本,这样操作有点不合理,但是在不加额外的人工标注的情况下,这也是我们能做到的最优的思路了。
训练语料还有一个问题答案的同义词问题,比如问“憨豆的扮演者”,标准答案是“罗温艾金森”,但是材料中不仅有“罗温艾金森”,还有“罗温·艾金森”、“罗温.艾金森”、“洛温·艾金森”等。SOGOU比赛比较好的一点是它提供了一个相对客观的线下评测脚本,这个评测脚本考虑了同义词的变化,因此我们可以从这个评测脚本中找到答案的同义词,从而可以把同义答案都标注出来。
还有一些诸如全角字符转半角的操作,相信大家看了数据集自然也就想到了,因此不再赘述。
数据打匀 #
SOGOU最后一共提供了3万个问题的标注语料,并且给我们预先划分好了训练集(2.5万)和验证集(0.5万)。但是如果直接用它的划分来训练,那验证集的结构却跟线上提交的结果出入比较大。
所以我们把所有的标注语料混合然后重新打乱,并且重新划分训练集(2万)和验证集(1万),这样在验证集上的得分约为0.76,跟线上提交的结果接近。
数据扩增 #
在模型的训练过程中,使用了可以称得上是数据扩增的三个操作。
1、直接随机地将问题和材料的部分词id置零:问题和材料都是以词id序列的方式输入,0是填充符(相当于
),随机置零就是随机将词用 替换,减弱对部分词的依赖; 2、将同一段材料通过重复拼接、随机裁剪的方式,来得到新的材料(答案的数目、位置也随之变化);
3、对于答案出现多次的材料,随机去掉某些答案的标注。比如答案“广东”可能在某段材料中出现两次,那么做答案标注的时候,可能只标注第一个、或只标注第二个、或都标注。
印象中,第1个数据扩增手段影响比较大的,能有效提升模型的稳定性和精度,至于第2、3个方案相对微弱一些。第1个数据扩增手段,跟直接对词向量序列进行dropout的区别是:dropout除了随机置零外,还会进行尺度缩放,而这里就是不想要它的尺度缩放,解释性要好些。
解码策略 #
很多参赛选手可能会忽略的一个细节是:答案的解码方式可能有很大的优化空间,而优化解码带来的提升,可能远比反复对模型调参带来的提升要大!
打分方式 #
何为答案解码?不管是用softmax形式的指针,还是用本文的sigmoid形式的“半指针-半标注”,最后模型输出的是两列浮点数,分别代表了答案起始位置和终止位置的打分。但问题是,用什么指标确定答案区间呢?一般的做法是:确定答案的最大长度max_words(我取了10,但汉字算一个,字母和数字只算半个),然后遍历材料所有长度不超过max_words的区间,计算它们起始位置和终止位置的打分的和或积,然后取最大值。那么问题来了,“和”好还是“积”好呢?又或者是“积的平方根”?
开始我按直觉来,感觉“积的平方根”是最合理的,后来测试了一下直接改成“积”,发现效果提升很明显(1%)。于是我就反复斟酌了这个解码决策过程,发现里面还其实有很多坑,这也是一种重要的超参,不能单纯按照直觉来。
投票方式 #
比如同一段材料同一个片段出现多次时,是要把这些片段的打分求和、求平均还是只取最大的?每段材料都得到了自己的答案,又怎么把这么多段材料的答案投票出最终的答案来?
比如有5段材料,每段材料得出的答案和分数依次是(A, 0.7)、(B, 0.2)、(B, 0.2)、(B, 0.2)、(B, 0.2),那么我们最终应该输出A还是B呢?有人说“三个臭皮匠,顶一个诸葛亮”,自然这里的臭皮匠指的是指低分答案B,诸葛亮是指高分答案A,4个B的分数加起来为0.8 > 0.7,这样看起来应该输出B?
我觉得不大对。在我们的生活中,专家并不等于平民的简单叠加,人多的确力量大,但很多时候$1+1$是小于$2$的。就好比上面的答案分布,我们其实更倾向于选择A答案,因为它接近满分1,而且相对其它答案更加“出类拔萃”。
所以,我们的投票方式必须体现两点:1、人多力量大;2、$1+1 < 2$。所以求和以及求平均都不行,最简单的方案应该是“平方和”
1、对于同一段材料,如果一个片段出现了多次,那么只取最大的那个分,不平均也不求和,这是因为“同一段材料”相当于“同一个人”,同一个人就没必要叠加太多了;
2、经过这样处理,每段材料都“选举”出自己的答案了,每段材料就相当于一个“臭皮匠”或“诸葛亮”,每个答案都有自己的分数,就是代表这些“臭皮匠”或“诸葛亮”的决策,将相同答案的打分求“平方和”作为该答案的最后打分,然后在不同答案中选最大的那个:
$$s_a = \sum_{i=1}^n s^2_{a,i}$$
因为“平方”会把高分的样本权重放大。3、相比步骤2,我在比赛中使用了一个略微不同的打分公式:
$$s_a = \frac{\sum\limits_{i=1}^n s^2_{a,i}}{1+\sum\limits_{i=1}^n s_{a,i}}$$
这个公式同样是平方求和的思想,只是再求了一次平均,并且分母“+1”。“平方”这个操作是对专家的加权,“+1”则是对小样本的惩罚,这个公式比直接平方求和更加平缓。
注意,不仅仅是我们的模型,我在跟另外一参赛选手交流的时候,提示了他这个解码方式,他用同样的思路经过调试后,也得到了比较大的提升~
模型融合 #
经过上述步骤,模型在SOGOU的在线测试集上达到0.74~0.75的分数应该是没有问题的。但要达到最优的0.7583,就要上模型融合了。
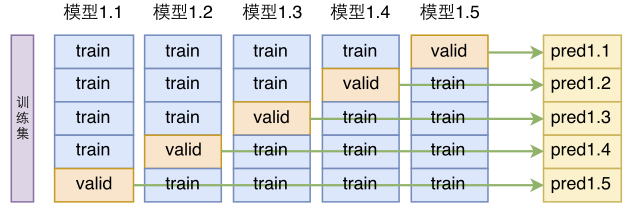
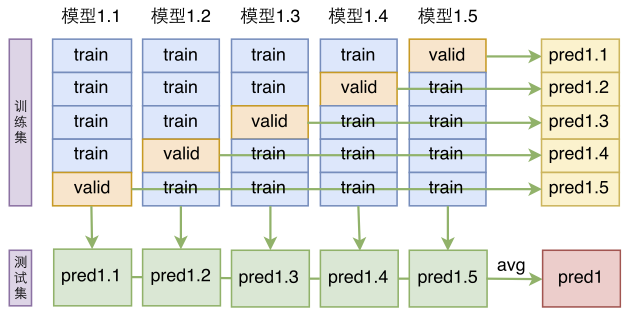
模型融合分单模型融合和多模型融合。单模型融合是指同一个模型架构,用不同的方式训练多次,然后将结果平均;多模型融合则是给每个模型都做一次单模型融合,然后将多个单模型融合的结果再次融合。简单起见,我们只做了单模型融合。
单模型建立在交叉验证的基础上。前面我们提到,将标注语料重新打乱后,重新划分训练集和验证集,交叉验证的话更彻底一些,它把标注语料重新打乱后,分为$k$份,每份都拿来做一次验证集(每次都要重零开始训练模型)
这样一来,我们就得到了同一个模型的$k$个不同训练结果,然后将这些结果平均一下,就是模型融合了:
后文 #
效果评估 #
排行榜摆在那,所以模型的效果是看得见的,在SOGOU这个噪声这么大的封闭测试集上,我们模型最终得分都有0.7583,而且从训练集来开,我觉得有些噪声是故意加进去的,有些材料实在太离谱,感觉直接放在搜索引擎或百度知道召回一批材料都不至于这么糟糕,所以我认为实际使用中效果会更好。再加上纯CNN的轻量级模型,这已经完全满足工业需求了。
另外,我也在SQUAD上测了一下这个模型,发现准确率也就50%上下,不过没精调,也没融合。如果经过优化调试,估计也就60%+的准确率吧。显然这跟0.7583的得分差距是比较远的,这也表明WebQA式的阅读理解问答,跟SQUAD的纯阅读理解,是很不一样的,虽然理论上它们的模型可以相互套用。
代码&测试 #
模型已经上线到火焰科技的官网上,可以点击这个链接在线测试:
http://www.birdbot.cn/online-factual-qa.html
(移动端访问效果也许欠佳,请尽量在PC端访问。^_^)
至于代码就不公开了,原因有两个。一是这个比赛是代表公司参加的,不好直接将所有东西开源,而且模型确实简单明快,看完文章后跟着文章实现并不难,如果读者还不能实现的话,我建议还是打好代码基础再玩阅读理解和问答系统;二是一旦开源,总有那么些读者连文章都不想看,直接把代码下载下来,然后跑不通就一连串问题“这个库怎么安装”、“这句代码又报错了”,实在应接不暇。
这篇文章终究不是扫盲文,所以请读者们见谅。当然,没有歧视初学者的意思,博客也时常会有入门级的文章出现,只不过不是这篇罢了。
此外,作为一个及格的参赛者,SOGOU的训练语料也不好直接公开,需要测试的读者,可以直接用WebQA数据集进行训练。
千调百试 #
最后给大家看个截图
这个截图基本上就代表了我的整个调试过程了,其中包含了上百次的迭代调试,每次更新又要做多次实验~这是我目前做比赛最投入的一次了。
所以,虽然本文不是正式的paper,但如果读者确实从本文中收获了什么,那么希望能引用一下本文。
最后的最后,感谢广州火焰科技提供的软件和硬件上的的支持,公司给我提供了非常友好的发展和成长的机会~
PS:后来发现,本文的模型其实跟《Fast Reading Comprehension with ConvNets》和《QANET: Combining Local Convolution with Global Self-Attention for Reading Comprehension》这两篇论文“撞车”了,但笔者当初做比赛时,确实从未参考过这两篇论文。当时是从WebQA的论文出发,打算复现WebQA的模型,然后觉得好奇就想试试CNN模型,然后就一发不可收了。
转载到请包括本文地址:https://spaces.ac.cn/archives/5409
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Apr. 15, 2018). 《基于CNN的阅读理解式问答模型:DGCNN 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/5409
@online{kexuefm-5409,
title={基于CNN的阅读理解式问答模型:DGCNN},
author={苏剑林},
year={2018},
month={Apr},
url={\url{https://spaces.ac.cn/archives/5409}},
}












May 10th, 2018
@Mason|comment-9127
建议检查模型有无写错
您好:
我的模型大概检查了3遍,应该没什么问题。这个模型复现了2周了,能否把模型构建的核心代码(只要模型搭建就可以)发我对比一下,感觉没找到什么问题,感谢。
May 16th, 2018
1.文中提到:
为了增加模型的“大局观”,我们将材料的序列编码为一个整体的向量……
请问苏老师,这个Encoder是个什么结构?
2.图示给出的各层卷积之后,好像是没有BN或者其他的norm。请问苏老师,如果卷积层数更深的话,是否需要加上更好,如果需要,选用何种norm可能会更合理一些?
encoder实际上就是本文的
https://kexue.fm/archives/5409#注意力
部分。
此外,我试过在原模型上用BN,效果还有轻微下降。我个人是觉得BN太丑,所以不管是图像还是文本模型,我是能不用BN就不用BN。
我记得Facebook的论文中用过layer norm,我也试了一下,没提升,但收敛快了,所以用norm的话,推荐用layer norm。
May 21st, 2018
博主你好,这篇文章的attention模型只需要question embedding作为输入,但是R-Net模型的attention是把question embedding和passage embedding都作为输入,我理解的attention模型也是需要结合二者的输入才能确定哪部分文本是重要的,请问你当时设计模型时是做了什么特殊考量吗?
因为这个模型只需要一个最基本的encoder,生成一个句向量。
试想一下,给你一个句子,你也可以提取这个句子的关键词,这不需要任何的外部知识(不需要passage)。还有,之前有论文提出,直接用seq2seq的机器翻译模型的encoder部分做句向量,这个encoder生成的句向量,也不需要外部知识。
同时输入question和passage做attention,其实起到了减轻模型学习难度的作用,相当于一种因地制宜的encoder。但本文处理的问题,偏检索性,难度并没有那么高,encoder也不需要太复杂。
June 6th, 2018
苏神,方便共享一下训练好的词向量么?
June 6th, 2018
博主你好,请问Conv1D Block残差结构那里相加之后有用激活函数激活吗?
不用,GCNN的门结构,本身就算一个激活函数了
June 6th, 2018
已经找到共享了,谢谢提供,怪我没仔细搜索。 :)
哪里有?
June 10th, 2018
请问attention那里公式(5)β指的是什么呢?
就是一个训练参数,全连接层的偏置项
那α⊤Act(Wxi+b)中alpha的转置和Act是矩阵乘法还是element-wise乘法?
矩阵乘法(在这里事实上就是内积)
June 10th, 2018
博主,你的模型总图非常像做英语阅读理解的一种模式“带着问题去阅读文章”,我觉得也可以像做阅读理解的另一种模式“阅读完文章去做题”,然后将这两种模式结合,感觉会更好。
你的理解是对的。只是这个要看问题面向的场景,因为这里的场景基本上是简单的检索型,所以做到这个程度很大程度上已经满足需求了
June 11th, 2018
博主,如果数据集中出现了较多的错别字(比如白云山和白芸山),该怎么处理呢
June 25th, 2018
你好,我想问两个问题:
1.最后的标注网络是怎样处理的呢?是直接在attention后加两层LSTM还是有其他方案呢?
2.如果好的网络,想自己写问题放进去预测,是不是需要做问题相似度的问题?
谢谢~
请入门后再仔细看本文~
事实上你问的问题在本文基本上都已经讲清楚了。