路径积分系列：3.路径积分

路径积分是量子力学的一种描述方法，源于物理学家费曼[5]，它是一种泛函积分，它已经成为现代量子理论的主流形式. 近年来，研究人员对它的兴趣愈发增加，尤其是它在量子领域以外的应用，出现了一些著作，如[7]. 但在国内了解路径积分的人并不多，很多量子物理专业的学生可能并没有听说过路径积分.

从数学角度来看，路径积分是求偏微分方程的Green函数的一种方法. 我们知道，在偏微分方程的研究中，如果能够求出对应的Green函数，那么对偏微分方程的研究会大有帮助，而通常情况下Green函数并不容易求解. 但构建路径积分只需要无穷小时刻的Green函数，因此形式和概念上都相当简单.

本章并没有新的内容，只是做了一个尝试：从随机游走问题出发，给出路径积分的一个简明而直接的介绍，展示了如何将抛物型的偏微分方程问题转化为路径积分形式.

从点的概率到路径的概率 #

在上一章对随机游走的研究中，我们得出从$x_0$出发，$t$时间后，走到$x_n$处的概率密度为
$$\frac{1}{\sqrt{2\pi \alpha T}}\exp\left(-\frac{(x_n-x_0)^2}{2\alpha t}\right).\tag{22}$$
这是某时刻某点到另一个时刻另一点的概率，在数学上，我们称之为扩散方程$(21)$的传播子，或者Green函数.

现在把时间等分为$n$分，每份长度为$\Delta t=\frac{T}{n}$，在$i\Delta t$时刻，粒子的位置位于$x_k$. 粒子从$x_k$到达$x_{k+1}$的概率密度为
$$\frac{1}{\sqrt{2\pi \alpha \Delta t}}\exp\left(-\frac{(x_{k+1}-x_k)^2}{2\alpha \Delta t}\right),\tag{23}$$
所以粒子依次经过$x_1,x_2,\dots,x_{n-1},x_n$的概率密度为
$$\left(\frac{1}{\sqrt{2\pi \alpha \Delta t}}\right)^n\exp\left(-\frac{(x_1-x_0)^2+(x_2-x_1)^2+\dots+(x_n-x_{n-1})^2}{2\alpha \Delta t}\right),\tag{24}$$
暂时省略前面的因子，然后取$\Delta t\to 0$的极限，我们认为$x_0,x_1,x_2,\dots,x_{n-1},x_n$这些点，确定了一条从$(x_0,0)$到$(x_n,T)$的路径$x(t)$，而
$$\frac{(x_1-x_0)^2+(x_2-x_1)^2+\dots+(x_n-x_{n-1})^2}{2\alpha \Delta t}=\frac{1}{2\alpha}\sum_{k=0}^{n-1} \left(\frac{x_{k+1}-x_k}{\Delta t}\right)^2\Delta t,\tag{25}$$
在$\Delta \to 0$时，我们认为$\frac{x_{k+1}-x_k}{\Delta t}$等于$x(t)$在$t_k$的导数$\dot{x}(t_k)$，这样上式正是积分$\frac{1}{2\alpha}\int\dot{x}^2dt$的离散表达式. 综上，我们得到粒子沿着路径$x=x(t)$走过的概率，正比于
$$P[x(t)] = \exp\left(-\frac{1}{2\alpha }\int\dot{x}^2dt\right).\tag{26}$$
这就得到了粒子经过路径$x(t)$的概率，它是关于$x(t)$的泛函. 这也就是布朗运动的路径概率分布. 其中，如果$\alpha=1$，那么称之为标准布朗运动.

注释：

如果$W_t$是一个随机过程，满足以下条件，那么称之为一个布朗运动：
1、$W_0=0$；
2、$\{W_t,t\geq 0\}$是平稳的独立增量过程；
3、$\forall 0\leq s\leq t$，$W_t-W_s \sim N(0,\sigma^2(t-s))$.
当$\sigma=1$时，称之为标准布朗运动.

对路径进行求和 #

我们已经得到了某条路径的概率$P[x(t)]$的表达式，那么从$(x_0,0)$到$(x_n,T)$的概率，应该是$(x_0,0)$到$(x_n,T)$的所有路径的概率之和. 换言之，我们要遍历两点间的所有路径求和.

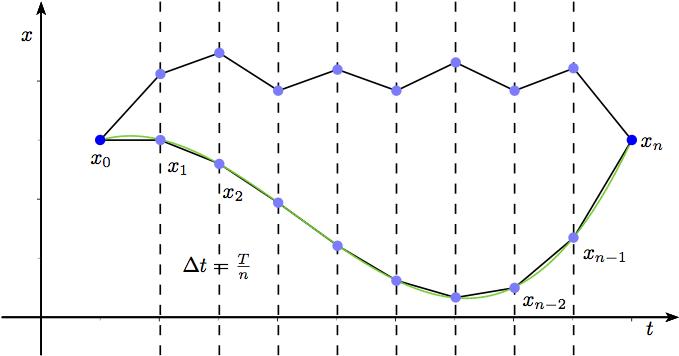
遍历是通过离散化路径来实现的，如图1所示，依然将时间$T$进行划分，对于每一条路径，我们都可以用折线$x_0,x_1,x_2,\dots,x_{n-2},x_{n-1},x_n$来逼近它，因此，如果要遍历所有路径$x(t)$，那么只需要遍历所有$x_1,x_2,\dots,x_{n-2},x_{n-1}$（想象着上下“拨动”$x_1,x_2,\dots,x_{n-2},x_{n-1}$各点. ）.

离散化一条路径，然后遍历

如果用$P(x_0,0;x_n,T)$表示从$(x_0,0)$到达$x_n,T)$的概率，那么（简洁起见，我们省略了前面的常数因子，在实际问题中我们再恢复就行，现在我们先要把概念讲清楚）
$$\begin{aligned}&P(x_0,0;x_n,T)\\ =&\lim_{n\to\infty}\int_{-\infty}^{\infty} \exp\left(-\frac{1}{2\alpha}\sum_{k=0}^{n-1} \left(\frac{x_{k+1}-x_k}{\Delta t}\right)^2\Delta t\right)dx_1 dx_2\dots dx_{n-2}dx_{n-1}\end{aligned},\tag{27}$$
积分共有$n-1$次，然后取$n\to\infty$的极限. 我们把上式简记为
$$P(x_0,0;x_n,T)=\int_{x_0}^{x_n} P[x(t)]\mathscr{D}x(t)=\int_{x_0}^{x_n} \exp\left(-\frac{1}{2\alpha }\int_0^T\dot{x}^2dt\right)\mathscr{D}x(t),\tag{28}$$
这称为泛函$P[x(t)]$的路径积分（或者叫泛函积分），这是一个无穷维的积分.

抛物方程的路径积分 #

本小节希望把抛物型方程$(19)$转换为路径积分表述，由$(27)$式可知，构造路径积分的关键是要找出无穷小时间间隔内的传播子（Green函数）.

首先考虑$V=V(x)$，即与时间无关的情况. 记$H=\frac{\alpha^2}{2}\frac{\partial^2}{\partial x^2}+ V$，将方程$(19)$简写为
$$\alpha\frac{\partial \phi}{\partial t} = H\phi,\tag{29}$$
因为$H$与$t$无关，那么上式的解可以形式地写为
$$\phi(x,t)=\exp\left(\frac{1}{\alpha}t H\right)\phi(x,0)=\exp\left[\frac{1}{\alpha}t\left(\frac{\alpha^2}{2}\frac{\partial^2}{\partial x^2}+ V(x)\right)\right]\phi(x,0).\tag{30}$$

上述公式是精确解，其中$\exp\left(\frac{1}{\alpha}t H\right)$应该理解为算符级数
$$\exp\left(\frac{1}{\alpha}t H\right)=\sum_{k=0}^{\infty} \frac{1}{k!}\frac{t^k}{\alpha^k}H^k.\tag{31}$$

现在我们只关心在无穷小间隔的情况下的结果，即取$t=\epsilon\to 0$，那么
$$\phi(x,\epsilon)=\exp\left(\frac{\alpha}{2}\epsilon \frac{\partial^2}{\partial x^2}+\frac{1}{\alpha} \epsilon V(x)\right)\phi(x,0),\tag{32}$$
注意，$\frac{\partial^2}{\partial x^2}$与$V(x)$一般来说是不可交换的，所以一般来说
$$\exp\left(\frac{\alpha}{2}\epsilon \frac{\partial^2}{\partial x^2}+\frac{1}{\alpha} \epsilon V(x)\right)\neq \exp\left(\frac{\alpha}{2}\epsilon \frac{\partial^2}{\partial x^2}\right)\exp\left(\frac{1}{\alpha} \epsilon V(x)\right),\tag{33}$$
不过在一阶近似的情况下，两者是相等的（也就是说，两者的差是二阶无穷小的）. 所以我们有
$$\phi(x,\epsilon)=\exp\left(\frac{1}{\alpha} \epsilon V(x)\right)\exp\left(\frac{\alpha}{2}\epsilon \frac{\partial^2}{\partial x^2}\right)\phi(x,0),\tag{34}$$
留意到
$$\hat{\phi}(x,\epsilon) = \exp\left(\frac{\alpha}{2}\epsilon \frac{\partial^2}{\partial x^2}\right)\phi(x,0),\tag{35}$$
正好是扩散方程$\frac{\partial \hat{\phi}}{\partial t}=\frac{\alpha }{2}\frac{\partial^2 \hat{\phi}}{\partial x^2}$的形式解，而在数学物理教程中我们已经获得了它的通解：
$$\hat{\phi}(x,\epsilon)=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi\alpha\epsilon}}\exp\left(-\frac{1}{\alpha} \frac{(x-x_0)^2}{2\epsilon}\right)\phi(x_0,0)dx_0,\tag{36}$$
所以$(34)$式等于
$$\begin{aligned}\phi(x,\epsilon)=&\exp\left(\frac{1}{\alpha} \epsilon V(x)\right)\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi\alpha\epsilon}}\exp\left(-\frac{1}{\alpha} \frac{(x-x_0)^2}{2\epsilon}\right)\phi(x_0,0)dx_0\\ =&\frac{1}{\sqrt{2\pi\alpha\epsilon}}\int_{-\infty}^{\infty}\exp\left[-\frac{1}{\alpha} \left(\frac{1}{2}\frac{(x-x_0)^2}{\epsilon^2}-V(x)\right)\epsilon\right]\phi(x_0,0)dx_0\end{aligned},\tag{37}$$
由于上式是无穷小时间间隔下的，所以$\frac{x-x_0}{\epsilon}$可以认为是一阶导数$\dot{x}$，因此，无穷小时间内的Green函数为（省略前面的因子）
$$\exp\left[-\frac{1}{\alpha} \left(\frac{1}{2}\dot{x}^2-V(x)\right)\epsilon\right],\tag{38}$$
从而，我们可以相继地求得
$$\begin{aligned}&K(x_0,0;x_n,T)\\ =&\lim_{n\to\infty}\int_{-\infty}^{\infty} \exp\left\{-\frac{1}{2\alpha}\sum_{k=0}^{n-1} \left[\left(\frac{x_{k+1}-x_k}{\Delta t}\right)^2-V(x_k)\right]\Delta t\right\}dx_1 \dots dx_{n-1}\end{aligned},\tag{39}$$
由于$\phi$不是真正意义上的概率，因此这里用了$K$表示$\phi$的传播子. 上式也就意味着，经过某条路径$x(t)$的概率泛函是：
$$K[x(t)] = \exp\left[-\frac{1}{\alpha} \int_{t_a}^{t_b} \left(\frac{1}{2}\dot{x}^2-V(x)\right)dt\right],\tag{40}$$
这样就可以把从点$(x_a,t_a)$到点$(x_b,t_b)$的概率，表达为两点间的路径积分
$$\begin{aligned}P(x_b,t_b;x_a,t_a)=&\int_{x_a}^{x_b} P[x(t)]\mathscr{D}x(t) \\ =&\int_{x_a}^{x_b}\exp\left[-\frac{1}{\alpha} \int_{t_a}^{t_b} \left(\frac{1}{2}\dot{x}^2-V(x)\right)dt\right]\mathscr{D}x(t)\end{aligned}.\tag{41}$$
以上推导基于$V$与时间$t$无关的特例，但只需简单修改，就可以用于与时间相关情况的推导，这里不再赘述.

从路径积分到偏微分方程 #

从$(40)$的路径泛函出发，然后进行路径积分，可以反过来推导得到偏微分方程$(19)$，具体过程可以参考《量子力学与路径积分》，这里不再赘述. 既然它们之间可以相互推导，那么意味着两者是等价的，给出$(19)$形式的偏微分方程，立即可以对应地写出路径泛函$(40)$，反之亦然.

一些算例 #

路径积分在概念是相当简单，但计算却非常复杂，可精确算出的解非常少，很多时候仅仅是采用近似. 本节不加证明地给出一些结果，这些结果来自物理学家费曼所著的《量子力学与路径积分》、《统计力学讲义》等著作. 这里只是向读者展示，对于很多路径积分问题，都已经存在有效的计算方案.

最可能路径 #

我们已经接触了一些路径积分，它的形式是：
$$\int\exp\left(-\frac{1}{\alpha}S[x(t)]\right)\mathscr{D}(x(t).\tag{42}$$
其中$S[x(t)]$是$x(t)$的泛函，采用物理的说法，可以称它为“作用量”. 它的意义很明确，就是把所有路径的效应叠加起来. 很自然会考虑的一个问题是：哪条路径的贡献最大？如果这个效应是概率，那么这个问题就相当于问哪条路径的概率最大？

很明显，如果要$\exp\left(-\frac{1}{\alpha}S[x(t)]\right)$尽可能大，那么希望$S[x(t)]$尽可能小，但是这个并不够充分，充分的条件是$S[x(t)]$在$x(t)$附近要尽可能平稳，这样才能使得$x(t)$的贡献能够稳定地叠加起来. 在这里，“稳定”的意思是$S[x(t)]$的一阶变分为0. 由此我们看到，路径积分的最可能路径问题，很自然地给出了一个“变分原理”，这表明变分原理与路径积分有着密切的联系.

对于我们前面讨论的
$$S[x(t)]=\int_{t_a}^{t_b}\left[\frac{1}{2}\dot{x}^2-V(x,t)\right]dt,\tag{43}$$
$\delta S[x(t)]=0$给出
$$\ddot{x}=-\frac{\partial V}{\partial x}.\tag{44}$$
边界条件为$x(t_a)=x_a,x(t_b)=x_b$，设其解为$x_{cl}(t)$，将解代入$S[x(t)]$中，可以算得一个$S_{cl}$，它是$t_a,t_b,x_a,x_b$的函数，这些记号在求解二次型问题中会有帮助.

对于随机游走对应的$V(x,t)$，有
$$\ddot{x}=\frac{1}{2}\alpha\frac{\partial^2 p}{\partial x^2}+p\frac{\partial p}{\partial x}+\alpha \frac{\partial p}{\partial t}.\tag{45}$$

二次型作用量 #

对于任意的二次型作用量，路径积分是可以精确求解的，答案是：
$$P(b,a)=\left(\frac{1}{2\pi \hbar}\right)^{D/2} \sqrt{-\det\left(\frac{\partial^2 S_{cl}}{\partial x_a \partial x_b}\right)}\exp\left(-\frac{1}{\hbar}S_{cl}\right),\tag{46}$$
其中$D$是空间的维数，而$\det\left(\frac{\partial^2 S_{cl}}{\partial x_a \partial x_b}\right)$被称为van Vleck-Pauli-Morette 行列式。证明过程可以参考[6].

微扰展开 #

对于无法精确计算的作用量的路径积分，有微扰展开式
$$P(b,a)=P_0(b,a)+\left(-\frac{1}{\hbar}\right)\int P(b,c)V(c)P(c,a) d\tau_c+\left(-\frac{1}{\hbar}\right)^2\int P(b,d)V(d)P(d,c)V(c)P(c,a) d\tau_c d\tau_d. \tag{47}$$
具体的符号含义和推导，都可以参考费曼的著作[5].

转载到请包括本文地址：https://spaces.ac.cn/archives/3757

更详细的转载事宜请参考：《科学空间FAQ》