对称多项式不等式的“物理证明”
By 苏剑林 | 2011-08-13 | 46338位读者 | 引用本文将再次谈到对称这个话题,不过这一次的对象不是“等式”,而是“不等式”。
在数学研究中,我们经常会遇到各种各样的函数式子,其中有相当一部分是“对称”的。什么是对称的函数呢?对称有很多种说法,但是针对于多元对称式,我们的定义为满足$f(x_1,x_2,...,x_n)=f(y_1,y_2,...,y_n)$的函数,其中$(y_1,y_2,...,y_n)$是$(x_1,x_2,...,x_n)$的任意一个排列。通俗来讲,就是将式子中任意两个未知数交换位置,得到的式子还是和原来的式子一样。例如$\sin x+\sin y$,把$x,y$交换位置后得到$\sin y+\sin x$,还是和原来的一样;再如$xy+yz+zx$,将y,z互换后可以得到$xz+zy+yx$,结果还是和原式一样;等等。有些对称的函数是一个n次的多项式,那么就叫它为n次对称多项式,上边的例子$xz+zy+yx$就是一个三元二次对称多项式。
IMO42-1,我也会做几何题
By 苏剑林 | 2011-07-30 | 36581位读者 | 引用七月再次“农忙”,农村里要插秧了,播下种苗,等待再次收获的季节^_^
我一直觉得我的数学能力偏向于分析计算而不擅长于几何,纵使遇到几何问题,也是满脑子的解析几何做法,没有纯几何的美。而这几天为了加强数学竞赛题目的能力,我一直在看IMO的题目,并且企图独立做出一些题目,但都无果。我比较感兴趣的是不等式,我感觉一道简单的式子,不用太多的文字就可以讲清楚的题目非不等式莫属,但是IMO的不等式题实在高深,我还没有能够独立做出一道来(参考答案可以看懂,只是想不到思路),或许是我在努力追求统一的方法而不肯研究那些特定的技巧的原因吧。不料今天看了一下2001年IMO的几何题目,发现我可能将它做出来,于是研究了一会,最终很幸运地做了出来。虽然不是最简单的方法,但也与大家分享一下。
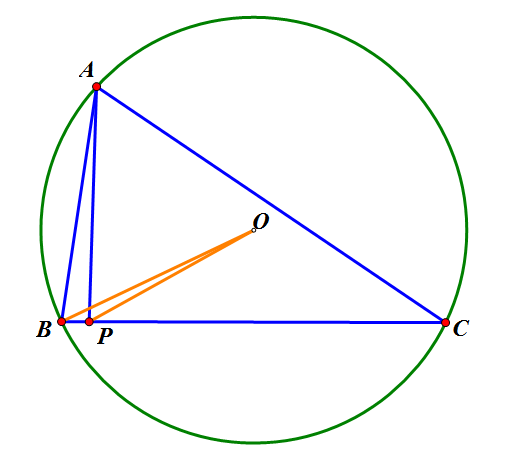
如图,O是锐角三角形ABC的外心,AP是三角形的垂线段,∠B-∠C不小于30°。证明∠BAC+∠BOP < 90°
[更正]一道经典不等式的美妙证明
By 苏剑林 | 2011-07-20 | 29040位读者 | 引用在数学竞赛中,很多题目都专门设置了一种技巧,这种技巧在很大程度上是不怎么理所当然的,换句话说,难以“顺理成章”地想下去,或者是说方法不成系统的,这也是我有点不喜欢数学竞赛题目的一个原因。当然,另一方面,个人认为数学竞赛比物理竞赛更能锻炼一个人的思维能力,尤其是在抽象思维以及几何想象能力等,因此做一些这样的题目也会有好处的。
下面就是一道很经典的竞赛题,它是在韩国举行的第42届IMO中的题目:
设a,b,c都是正实数,求证:
$\frac{a}{\sqrt{a^2+8bc}}+ \frac{b}{\sqrt{b^2+8ac}} + \frac{c}{\sqrt{c^2+8ab}} \geq 1$
中国队2010年再获IMO团体总分第一
By 苏剑林 | 2010-07-21 | 25545位读者 | 引用IMO,International Mathematical Olympiad,国际数学奥品匹克竞赛,是中学数学最高水平的国际比赛,由东欧国家发起。是为全球高中学生举办的世界最高水平的数学赛事。BoJone对它很感兴趣,不过它过于注重纯数学,应用数学少,致使BoJone不愿意放太多精力下去,因为我始终对具有明显的实际应用意义的数学和物理更感兴趣。
2010年7月2-14日在哈萨克斯坦共和国首都阿斯塔纳举行的第51届国际数学奥林匹克竞赛中,中国队6名参赛选手全部获得金牌,其中来自上海的Nie Zipei同学以本届惟一一个取得满分42分的成绩,而荣获绝对冠军,另外,Jialun Li为36分、Yikang Xiao为34分、Min Zhang为30分、Li Lai 为28分、Su Jun 为27分;中国队以总分197分(满分252),连续三年获得团体总分第一名(2007年获得亚军);中国队自1985年以来参赛25次,共获得过16次冠军;1998年未参加在台湾举行的比赛。本届比赛,俄罗斯队以169分获得亚军,美国队以一分之差屈居季军。









最近评论