ReLU/GeLU/Swish的一个恒等式
By 苏剑林 | 2025-08-16 | 28005位读者 | 引用今天水一点轻松的内容,它基于笔者这两天意识到的一个恒等式。这个恒等式实际上很简单,但初看之下会有点意料之外的感觉,所以来记录一下。
基本结果
我们知道$\newcommand{relu}{\mathop{\text{relu}}}\relu(x) = \max(x, 0)$,容易证明如下恒等式
\begin{equation}x = \relu(x) - \relu(-x)\end{equation}
如果$x$是一个向量,那么上式就更直观了,$\relu(x)$是提取出$x$的正分量,$- \relu(-x)$是提取出$x$的负分量,两者相加就得到原本的向量。
BN究竟起了什么作用?一个闭门造车的分析
By 苏剑林 | 2019-10-11 | 171776位读者 | 引用BN,也就是Batch Normalization,是当前深度学习模型(尤其是视觉相关模型)的一个相当重要的技巧,它能加速训练,甚至有一定的抗过拟合作用,还允许我们用更大的学习率,总的来说颇多好处(前提是你跑得起较大的batch size)。
那BN究竟是怎么起作用呢?早期的解释主要是基于概率分布的,大概意思是将每一层的输入分布都归一化到$\mathcal{N}(0,1)$上,减少了所谓的Internal Covariate Shift,从而稳定乃至加速了训练。这种解释看上去没什么毛病,但细思之下其实有问题的:不管哪一层的输入都不可能严格满足正态分布,从而单纯地将均值方差标准化无法实现标准分布$\mathcal{N}(0,1)$;其次,就算能做到$\mathcal{N}(0,1)$,这种诠释也无法进一步解释其他归一化手段(如Instance Normalization、Layer Normalization)起作用的原因。
在去年的论文《How Does Batch Normalization Help Optimization?》里边,作者明确地提出了上述质疑,否定了原来的一些观点,并提出了自己关于BN的新理解:他们认为BN主要作用是使得整个损失函数的landscape更为平滑,从而使得我们可以更平稳地进行训练。
本博文主要也是分享这篇论文的结论,但论述方法是笔者“闭门造车”地构思的。窃认为原论文的论述过于晦涩了,尤其是数学部分太不好理解,所以本文试图尽可能直观地表达同样观点。
(注:阅读本文之前,请确保你已经清楚知道BN是什么,本文不再重复介绍BN的概念和流程。)
浅谈神经网络中激活函数的设计
By 苏剑林 | 2017-10-26 | 61104位读者 | 引用激活函数是神经网络中非线性的来源,因为如果去掉这些函数,那么整个网络就只剩下线性运算,线性运算的复合还是线性运算的,最终的效果只相当于单层的线性模型。
那么,常见的激活函数有哪些呢?或者说,激活函数的选择有哪些指导原则呢?是不是任意的非线性函数都可以做激活函数呢?
这里探究的激活函数是中间层的激活函数,而不是输出的激活函数。最后的输出一般会有特定的激活函数,不能随意改变,比如二分类一般用sigmoid函数激活,多分类一般用softmax激活,等等;相比之下,中间层的激活函数选择余地更大一些。
浮点误差都行!
理论上来说,只要是非线性函数,都有做激活函数的可能性,一个很有说服力的例子是,最近OpenAI成功地利用了浮点误差来做激活函数,其中的细节,请阅读OpenAI的博客:
https://blog.openai.com/nonlinear-computation-in-linear-networks/
或者阅读机器之心的介绍:
https://mp.weixin.qq.com/s/PBRzS4Ol_Zst35XKrEpxdw
开学啦!咱们来做完形填空~(讯飞杯)
By 苏剑林 | 2017-09-03 | 249335位读者 | 引用前言
从今年开始,CCL会议将计划同步举办评测活动。笔者这段时间在一创业公司实习,公司也报名参加这个评测,最后实现上就落在我这里,今年的评测任务是阅读理解,名曰《第一届“讯飞杯”中文机器阅读理解评测》。虽说是阅读理解,但事实上任务比较简单,是属于完形填空类型的,即一段材料中挖了一个空,从上下文中选一个词来填入这个空中。最后我们的模型是单系统排名第6,验证集准确率为73.55%,测试集准确率为75.77%,大家可以在这里观摩排行榜。(“广州火焰信息科技有限公司”就是文本的模型)
事实上,这个数据集和任务格式是哈工大去年提出的,所以这次的评测也是哈工大跟科大讯飞一起联合举办的。哈工大去年的论文《Consensus Attention-based Neural Networks for Chinese Reading Comprehension》就研究过另一个同样格式但不同内容的数据集,是用通用的阅读理解模型做的(通用的阅读理解是指给出材料和问题,从材料中找到问题的答案,完形填空可以认为是通用阅读理解的一个非常小的子集)。
虽然,在这次评测任务的介绍中,评测方总有意无意地引导我们将这个问题理解为阅读理解问题。但笔者觉得,阅读理解本身就难得多,这个就一完形填空,只要把它作为纯粹的完形填空题做就是了,所以本文仅仅是采用类似语言模型的做法来做。这种做法的好处是思路简明直观,计算量低(在笔者的GTX1060上可以跑到batch size为160),便于实验。
模型
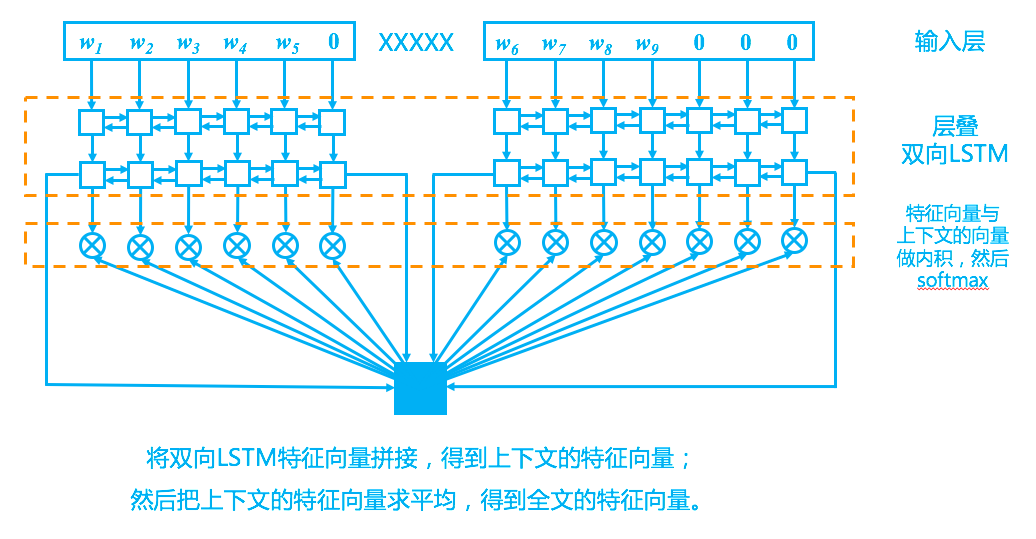
回到模型上,我们的模型其实比较简单,完全紧扣了“从上下文中选一个词来填空”这一思想,示意图如下。
fashion mnist的一个baseline (MobileNet 95%)
By 苏剑林 | 2017-08-27 | 98817位读者 | 引用浅尝
昨天简单试了一下在fashion mnist的gan模型,发现还能work,当然那个尝试也没什么技术水平,就是把原来的脚本改一下路径跑了就完事。今天回到fashion mnist本身的主要任务——10分类,用Keras测了一下一些模型在上面的分类效果,最后得到了94.5%左右的准确率,加上随机翻转的数据扩增能做到95%。
首先随便手写了一些模型的组合,测试发现准确率都不大好,看来对于这个数据集来说,自己构思模型是比较困难的了,于是想着用现成的模型结构。一说到现成的cnn模型,基本上我们都会想到VGG、ResNet、inception、Xception等,但这些模型为解决imagenet的1000分类问题而设计,用到这个入门级别的数据集上似乎过于庞大了,而且也容易过拟合。后来突然想起,Keras好像自带了个叫MobileNet的模型,查看了一下模型权重,发现参数量不大,但是容量应该还是可以的,故选用MobileNet做实验。
深究
从Boosting学习到神经网络:看山是山?
By 苏剑林 | 2016-07-01 | 88574位读者 | 引用前段时间在潮州给韩师的同学讲文本挖掘之余,涉猎到了Boosting学习算法,并且做了一番头脑风暴,最后把Boosting学习算法的一些本质特征思考清楚了,而且得到一些意外的结果,比如说AdaBoost算法的一些理论证明也可以用来解释神经网络模型这么强大。
AdaBoost算法
Boosting学习,属于组合模型的范畴,当然,与其说它是一个算法,倒不如说是一种解决问题的思路。以有监督的分类问题为例,它说的是可以把弱的分类器(只要准确率严格大于随机分类器)通过某种方式组合起来,就可以得到一个很优秀的分类器(理论上准确率可以100%)。AdaBoost算法是Boosting算法的一个例子,由Schapire在1996年提出,它构造了一种Boosting学习的明确的方案,并且从理论上给出了关于错误率的证明。
以二分类问题为例子,假设我们有一批样本$\{x_i,y_i\},i=1,2,\dots,n$,其中$x_i$是样本数据,有可能是多维度的输入,$y_i\in\{1,-1\}$为样本标签,这里用1和-1来描述样本标签而不是之前惯用的1和0,只是为了后面证明上的方便,没有什么特殊的含义。接着假设我们已经有了一个弱分类器$G(x)$,比如逻辑回归、SVM、决策树等,对分类器的唯一要求是它的准确率要严格大于随机(在二分类问题中就是要严格大于0.5),所谓严格大于,就是存在一个大于0的常数$\epsilon$,每次的准确率都不低于$\frac{1}{2}+\epsilon$。
OCR技术浅探:6. 光学识别
By 苏剑林 | 2016-06-25 | 89503位读者 | 引用经过第一、二步,我们已经能够找出图像中单个文字的区域,接下来可以建立相应的模型对单字进行识别.
模型选择
在模型方面,我们选择了深度学习中的卷积神经网络模型,通过多层卷积神经网络,构建了单字的识别模型.
卷积神经网络是人工神经网络的一种,已成为当前图像识别领域的主流模型. 它通过局部感知野和权值共享方法,降低了网络模型的复杂度,减少了权值的数量,在网络结构上更类似于生物神经网络,这也预示着它必然具有更优秀的效果. 事实上,我们选择卷积神经网络的主要原因有:
1. 对原始图像自动提取特征 卷积神经网络模型可以直接将原始图像进行输入,免除了传统模型的人工提取特征这一比较困难的核心部分;
2. 比传统模型更高的精度 比如在MNIST手写数字识别任务中,可以达到99%以上的精度,这远高于传统模型的精度;
3. 比传统模型更好的泛化能力 这意味着图像本身的形变(伸缩、旋转)以及图像上的噪音对识别的结果影响不明显,这正是一个良好的OCR系统所必需的.
闲聊:神经网络与深度学习
By 苏剑林 | 2015-06-06 | 99672位读者 | 引用在所有机器学习模型之中,也许最有趣、最深刻的便是神经网络模型了。笔者也想献丑一番,说一次神经网络。当然,本文并不打算从头开始介绍神经网络,只是谈谈我对神经网络的个人理解。如果希望进一步了解神经网络与深度学习的朋友,请移步阅读下面的教程:
http://deeplearning.stanford.edu/wiki/index.php/UFLDL教程
http://blog.csdn.net/zouxy09/article/details/8775360
机器分类
这里以分类工作为例,数据挖掘或机器学习中,有很多分类的问题,比如讲一句话的情况进行分类,粗略点可以分类为“积极”或“消极”,精细点分为开心、生气、忧伤等;另外一个典型的分类问题是手写数字识别,也就是将图片分为10类(0,1,2,3,4,5,6,7,8,9)。因此,也产生了很多分类的模型。








最近评论