站长注：这篇文章来源于网络，原文是繁体中文版本，我经过修改整理而成。它原来是《费曼的6堂Easy物理课》这本书的解说，但是由于内容上的详细和扼要，我更愿意把它当做物理学家费曼的解说，与大家分享。
伟哉！费曼
社会上普遍有种错误的想法，总以为科学是完全客观的，不但不会因人而异，更不会感情用事。对比之下，科学以外的各种人类活动，则多多少少会受到一般潮流动向、突发的时尚风潮，以及当事人的性格、偏好所左右。唯有科学，得受制于科学社群都同意的规则、步骤，与严密的测试、检验。科学仅着重于得到的结论，而不在乎谁是做研究、做实验的人。
以上说法显然是无稽之谈，科学既然靠人推动，就跟其他人类活动相同，都会受到大环境趋势及个人意念的影响。在科学领域，研究潮流的趋向受到主题素材选择的影响并不大，却相当取决于当时科学家对整个世界的看法。
最近在浏览“数学研发论坛”的时候，发现了一系列不等式手册，感觉是挺宝贵的资源，就把它转载到这里来了。
当然，里边的内容难度不一，很多东西我自己也未必用得上，甚至不能弄懂，不过还是放在这里保存，并与大家分享。
原文链接：http://bbs.emath.ac.cn/thread-1549-1-1.html
文件包内容：
152个未解决的问题.pdf
HLODER 与 MINKOWSKI不等式.pdf
不等式常用证法50种.pdf
不等式基本性质.pdf
单调函数不等式.pdf
调和函数不等式.pdf
多边形与多面体不等式.pdf
反三角函数不等式.pdf
级数不等式.pdf
数论不等式.pdf
农村的一个习俗就是孩子上大学了，一般要摆个大学酒，请亲朋好友们一起庆祝一番，说是光宗耀祖等等。那仪式好比婚礼仪式那样隆重......
这几天都是同学们摆大学酒的日子，10号去了东城镇喝老朱的大学酒，还要麻烦老朱他们免费接送，真的有点过意不去呀；11号是我自己的大学酒，叫了一群同学来，最后到场的有二十五个^_^，大家一起在村子礼堂二楼“包场”；12号是大宇和芬姐的，两边都答应了，所以中午去大宇那儿吃了一顿，下午去芬姐那玩了一番......
其实，于我们而言，大学酒就是一场同学们的聚会，藉着这个契机，我们昔日的同窗好友聚在一起，回忆过去，畅谈未来，讲述着我们那说不尽的友谊。我是很庆幸的一个人，三天四个人的大学酒都有我的参与，这至少给了我一些鼓励，这说明我的人际关系还不坏。谢谢邀请我的朋友们。也许很快我们就要真正地各分东西了，但是我相信，很多东西依然会存在我们的心中，那就像一条纽带，将我们紧紧联系在一起，如同天涯咫尺一般。
我相信，有很多地久天长的东西。
大学酒：
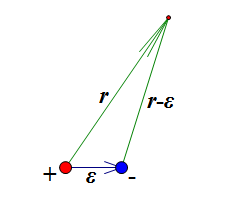
设想两个带有等量异号电荷的点电荷，它们之间的距离足够小，这样的一个模型被称为电偶极子（electric dipole）。我们研究电偶极子，主要是研究它在力学方面的性质。很多东西都可以用电偶极子来近似描述，比如一个小磁体周围的磁场，还有地球本身也可以近似看做一个偶极子来描述它的磁力情况，以及一些双原子分子的模型也被可以看做一个电偶极子模型，等等。在电偶极子模型中，两电荷的距离足够小，以至于我们忽略了一些关于距离的高次方项，只保留了线性部分，但对于物理探索来说，它已经足够精确，更重要的是，它足够简单，以至于我们可以容易把它清晰地描述出来。
我们先来研究电偶极子产生的电势。设它们各自的电荷量为q和-q，两者距离为ε，根据库仑定律，一个点电荷产生的电势，正比于该电荷的电荷量，同时反比于到该点电荷的距离。那么，一个电偶极子产生的电势为
$U=C(\frac{q}{r}+\frac{-q}{|\vec{r}-\vec{\varepsilon}|})$————(1)
21
Sep
军训结束了，基本在华师安家了
By 苏剑林 | 2012-09-21 | 16781位读者 | 引用上网的那些事儿
从申请帐号到接通校园网络，昨天晚上我总共花了将近3个小时才实现了在校内上网......
其实这本来不是一件很复杂的事情，但对于我的笔记本就是挺麻烦的。首先是申请，向隔壁师兄咨询了网管所在后，几分钟就申请到了账号，然后回到宿舍配置电脑。按照说明，是需要安装一个锐捷客户端的，通过手机把笔记本连上网络后，花了差不多20M流量下载了这个客户端，然后发现它竟然不能在Windows 8 64bit上运行。这就头疼了，我的笔记本只有Windows8和ubuntu呀，总不能为了上网换回Windows 7吧？就这样在两个系统中来来回回弄了两个小时，期间尝试过用mentohust来替换它，但发现在Windows 8上还是很头疼地不行。最后只能通过兼容模式来解决：
右击“锐捷客户端”的安装程序——属性——兼容性——选择以Windows 7兼容模式
右击“锐捷客户端”的安装程序——以管理员身份运行——安装程序——重新启动
然后就可以启动锐捷客户端了。我们用的是4.31版本。
在上一篇文章中，我们已经得到了电偶极子的等势面和电场线方程，这应该可以让我们对电偶极子的力场情况有个大致的了解了。当然，我们还是希望能够求出在这样的一个受力情况下，一个带电粒子是如何运动的。简单起见，在下面的探讨中，我们假定带电粒子的质量和电荷量均为1，至于电荷的正负，可以通过改变在$U=-\frac{k \cos\theta}{r^2}$中的k值的正负来控制。我们使用的工具依旧是理论力学中的欧拉-拉格朗日方程。
也许不少读者始终对公式感到头疼，更不用说是博大精深的理论力学了。但是请相信我，如果你花一点点心思去弄懂用变分法研究力学（或其他物理系统，但我目前只会用于力学）的基本思路和步骤，那么对你的物理研究是大有裨益的。因为在我眼中，学习了一丁点的理论力学知识后，我看到的只有物理的简洁与和谐。有兴趣的朋友可以看看我的那几篇《自然极值》等相关文章。
首先写出动能的表达式：$T=\frac{1}{2} (\dot{r}^2+r^2 \dot{\theta}^2)$
还有势能：$U=-\frac{k \cos\theta}{r^2}$
30
Aug
折腾windows 8和ubuntu 12
By 苏剑林 | 2012-08-30 | 20049位读者 | 引用这是一篇用Windows 8完成的文章。
快开学了，华师2号就要报道了，所以就提前入手一台手提电脑，联想Z575AM-ASI，四千元的AMD，4核，64位机器。
我的台式机已经是六年前的产品了，联想的家悦系列，只有512MB内存。所以相比之下，这新机器配置还过得去吧，对于CPU，我个人还是倾向于AMD的，因为我的那台家悦台式也是AMD的CPU，所以对它很有好感。新兴的联想专卖店没有AMD手提，所以还得提前向他们预订。
Windows8
手提本身没有预装操作系统，专卖店很随手地为我装了一个win7，而且还只是ghost版本的，时不时会卡死，感觉很不好，刚好前些日子在网上开始发布Windows8了，所以就马上把Win7格掉，装上Windows8了。安装过程很顺利，由于还没有正式发布，所以还没有激活，这段时间纯粹体验中。等正式版发布了，再计划买一个正版光盘吧
最近评论