科学空间|Scientific Spaces

（译自 陶哲轩 博客, 译者 liuxiaochuang）
（英文原文：Does one have to be a genius to do maths?）

这个问题的回答是一个大写的：不！为了达到对数学有一个良好的，有意义的贡献的目的，人们必须要刻苦努力；学好自己的领域，掌握一些其他领域的知识和工具；多问问题；多与其他数学工作者交流；要对数学有个宏观的把握。当然，一定水平的才智，耐心的要求，以及心智上的成熟性是必须的。但是，数学工作者绝不需要什么神奇的“天才”的基因，什么天生的洞察能力；不需要什么超自然的能力使自己总有灵感去出人意料的解决难题。

大众对数学家的形象有一个错误的认识：这些人似乎都使孤单离群的（甚至有一点疯癫）天才。他们不去关注其他同行的工作，不按常规的方式思考。他们总是能够获得无法解释的灵感（或者经过痛苦的挣扎之后突然获得），然后在所有的专家都一筹莫展的时候，在某个重大的问题上取得了突破的进展。这样浪漫的形象真够吸引人的，可是至少在现代数学学科中，这样的人或事是基本没有的。在数学中，我们的确有很多惊人的结论，深刻的定理，但是那都是经过几年，几十年，甚至几个世纪的积累，在很多优秀的或者伟大的数学家的努力之下一点一点得到的。每次从一个层次到另一个层次的理解加深的确都很不平凡，有些甚至是非常的出人意料。但尽管如此，这些成就也无不例外的建立在前人工作的基础之上，并不是全新的。（例如， Wiles 解决费马最后定理的工作，或者Perelman 解决庞加莱猜想的工作。）

点击阅读全文...

前几天在台湾购买（淘宝代购）的《费曼统计力学》和《费曼计算学》在今天到手了，至此，我的费曼著作收藏基本完成了。

我是一个费曼迷，为费曼的小飞侠人格所吸引，为费曼的物理才能所折服。因此，我甚至像普通人追星那样追崇费曼，收藏他的书籍，还有学习他所发明的物理。

点击阅读全文...

我小时候一直有个疑问：

直升机上的螺旋桨能不能用来挡雨？

一般的螺旋桨是若干个“条状”物通过旋转对称而形成的，也就是说，它并非一个面，按常理来说，它是没办法用来挡雨的。但是，如果在高速旋转的情况下，甚至假设旋转速度可以任意大，那么我们任意时刻都没有办法穿过它了，这种情况下，它似乎与一个实在的面无异？

力的无穷分解

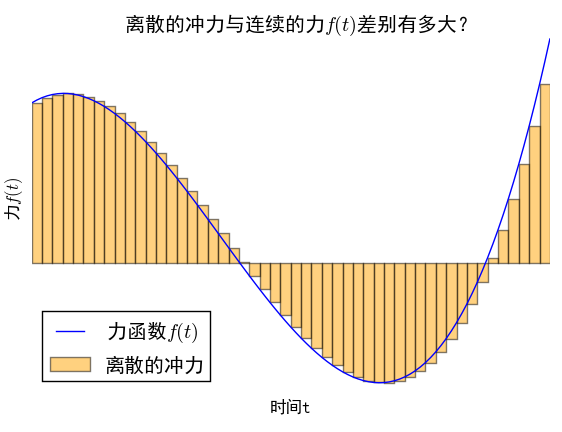
当然，以上只是笔者小时候的一个“异想天开”的念头，读者不必较真。不过，这个疑问跟本文有什么联系呢？我们在研究振动问题之时，通常会遇到在变力的作用下的受迫振动问题，已知变力是时间的函数，比如$f(t)$，然而，虽然知道$f(t)$的具体形式，但是由于$f$的非线性性，加上外力之后的运动，不一定容易求解。然而，如果可以将一个变化的力分段为无数个无穷小时间内的恒力（冲力），那么我们就可以分段讨论我们要研究的运动，而通常来说，恒力的问题会比变力容易。将一个变力离散化，然后再取极限，那么是不是跟原来在变力下的运动是一样的呢？这跟文章开头的疑问有着类似的思想——离线的极限，跟连续本身，是不是等价的？

而让人惊喜的是，在通常的物理系统中，将力分段为无数个小区间内的恒力的做法，能够导致正确的答案，而且，这恰好是线性常微分方程的格林函数法。下面我们来分析这一做法。

点击阅读全文...

昨晚上初等数论的时候，有这么一道题

求证
$$\frac{1}{3}x^3+\frac{1}{5}x^5+\frac{7}{15}x$$
恒为整数，其中$x$是一个整数。

更一般地，可以得到
$$\sum_{p\in\mathbb{P}}\frac{1}{p}x^p + \left(1-\sum_{p\in\mathbb{P}}\frac{1}{p}\right)x$$
恒为整数，其中$\mathbb{P}$是有限个素数的集合，还有更多整数值函数问题。要证明这些函数的值恒为整数，可以通过同余分析，证明分子总能被分母整除。但是，更妙的、同时往往会更简单的方法是，将结果赋予必然为整数的意义——可以是计算上的，也可以是操作上的。

点击阅读全文...

伽马函数
$$\Gamma(x)=\int_0^{+\infty}t^{x-1}e^{-t}dt$$
作为阶乘的推广，会让很多初学者感到困惑，对于笔者来说也不例外。一个最自然的问题就是：这般复杂的推广公式是如何得到的？

在cos.name的文章《神奇的伽马函数》中，有比较详细地对伽马函数的历史介绍，笔者细读之后也获益匪浅。但美中不足的是，笔者还是没能从中找到引出伽马函数的一种“自然”的办法。所谓“自然”，并不是说最简单的，而是根据一些基本的性质和定义，直接把伽马函数的表达式反解出来。它的过程和运算也许并不简单，但是思想应当是直接而简洁的。当然，我们不能苛求历史上伽马函数以这种方式诞生，但是作为事后探索是有益的，有助于我们了解伽马函数的特性。于是笔者尝试了以下途径，得到了一些结果，可是也得到了一些困惑。

点击阅读全文...

写在前面：本文是笔者数学建模课的作业，探讨了两生物种群竞争的常微分方程组模型的解的性质，展示了微分方程定性理论的基本思想。当然，本文最重要的目的，是展示LaTeX与Python的完美结合。（本文的图均由Python的Matplotlib模块生成；而文档则采用LaTeX编辑。）

问题提出

研究在同一个自然环境中生存的两个种群之间的竞争关系。假设两个种群独自在这个自然环境中生存时数量演变都服从Logistic规律，又假设当它们相互竞争时都会减慢对方数量的增长，增长速度的减小都与它们数量的乘积成正比。按照这样的假设建立的常微分方程模型为
$$\begin{equation}\label{eq:jingzhengfangcheng}\left\{\begin{aligned}\frac{dx_1}{dt}=r_1 x_1\left(1-\frac{x_1}{N_1}\right)-a_1 x_1 x_2 \\
\frac{dx_2}{dt}=r_2 x_2\left(1-\frac{x_2}{N_2}\right)-a_2 x_1 x_2\end{aligned}\right.\end{equation}$$
本文分别通过定量和定性两个角度来分析该方程的性质。

点击阅读全文...

前言：一年前国赛的时候，很初级地做了一下B题，做完之后还写了个《碎纸复原：一个人的数学建模》。当时就是对题目很有兴趣，然后通过一天的学习，基本完成了附件一二的代码，对附件三也只是有个概念。而今年我们上的数学建模课，老师把这道题作为大作业让我们做，于是我便再拾起了一年前的那份激情，继续那未完成的一个人的数学建模...

与去年不同的是，这次将所有代码用Python实现了，更简洁，更清晰，甚至可能更高效~~以下是论文全文。

研究背景

2011年10月29日，美国国防部高级研究计划局（DARPA）宣布了一场碎纸复原挑战赛（Shredder Challenge），旨在寻找到高效有效的算法，对碎纸机处理后的碎纸屑进行复原。[1]该竞赛吸引了全美9000支参赛队伍参与角逐，经过一个多月的时间，有一支队伍成功完成了官方的题目。

近年来，碎纸复原技术日益受到重视，它显示了在碎片中“还原真相”的可能性，表明我们可以从一些破碎的片段中“解密”出原始信息来。另一方面，该技术也和照片处理领域中的“全景图拼接技术”有一定联系，该技术是指通过若干张不同侧面的照片，合成一张完整的全景图。因此，分析研究碎纸复原技术，有着重要的意义。

点击阅读全文...

mnist的手写数字识别数据集一直是各种机器学习算法的试金石之一，最近有个新的数据集要向它叫板，称为fashion-mnist，内容是衣服鞋帽等分类。为了便于用户往fashion-mnist迁移，作者把数据集做成了几乎跟mnist手写数字识别数据集一模一样——同样数量、尺寸的图片，同样是10分类，甚至连数据打包和命名都跟mnist一样。看来fashion mnist为了取代mnist，也是拼了，下足了功夫，一切都做得一模一样，最大限度降低了使用成本～这叫板的心很坚定呀。

叫板的原因很简单——很多人吐槽，如果一个算法在mnist没用，那就一定没用了，但如果一个算法在mnist上有效，那它也不见得在真实问题中有效～也就是说，这个数据集太简单，没啥代表性。

fashion-mnist的github：https://github.com/zalandoresearch/fashion-mnist/

点击阅读全文...