哈勃定律——宇宙各向同性的体现
By 苏剑林 | 2010-10-04 | 24903位读者 | 引用1929年哈勃(Edwin Hubble)对河外星系的视向速度与距离的关系进行了研究。当时只有46个河外星系的视向速度可以利用,而其中仅有24个有推算出的距离,哈勃得出了视向速度与距离之间大致的线性正比关系。
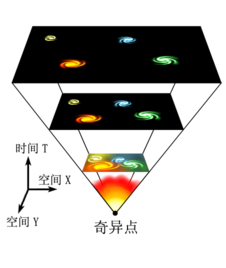
不少宇宙学的书籍中都提到了标题,那么,为什么哈勃定律是宇宙各向同性的体现?或者说为什么宇宙各向同性就必然导致哈勃定律?
首先我们得需要了解一下宇宙学原理,它告诉我们宇宙在大尺度范围是均匀的、各向同性的。基于这个原理,我们会得到一些很奇怪的东西,如宇宙中的每一点都是宇宙的中心。另外,我们还可以得到:宇宙的(整体)运动情况在每一个方向都应该取相同的形式。
《积分公式大全》网络版本
By 苏剑林 | 2010-10-06 | 22532位读者 | 引用为了方便各位读者查阅,BoJone特意制作了这个积分公式表的电子版本。
数学公式采用JsMath技术显示,为了能够更清晰地显示数学公式,推荐读者下载TeX-fonts字体。
原著的具体说明和下载,请点击
也许不少同好已经在一些书籍上看到过这样的论述:
各向同性的薄球壳,其内部任意一点所受到来自球壳的引力为0。
这是一个很神奇的事情,因为这意味着这是一个均匀引力场,虽然我们在很多问题上都假设了引力场均匀,但是我们却很难知道如何构造一个真正的均匀引力场(而构造一个真正的均匀力场都分析某些问题是很有用的,例如推导一些比例系数),现在眼前就摆着一个均匀引力场了。并且利用它我们就可以计算均匀实心球内部一点所受到的引力(等于它与一个球体的引力)。而关于它的证明,当然也可以利用微积分的知识,可是我们在这里介绍一个初等的方法,相信它会使我们更加感受到物理的神奇和有趣。
科学空间:2010年11月重要天象
By 苏剑林 | 2010-10-23 | 23918位读者 | 引用未来的天地枢纽——太空天梯
By 苏剑林 | 2010-10-22 | 26472位读者 | 引用漫话
BoJone认为,科学的意义并非在于无休止地计算,而是利用有限的科学理论来解释尽可能多的自然、生活现象。正因如此,科学家们追求和谐、简洁、优美的科学理论。科学就是想方设法地把未知变成已知,并在此基础上进一步发展。
随着媒体技术的发展,我们接触信息的渠道越来越多。每每我们从互联网或报纸上看到一则科学新闻时,我们几乎都会为之兴奋。但是,外行看热闹,内行看门道。对于真正热爱科学的朋友来说,也许会更加感兴趣新闻内容的来由。也就是说,我们希望进一步了解结论是怎样得出来的——哪怕只是在很浅的层面上认识。










最近评论